1.学习总结
1.1图的思维导图
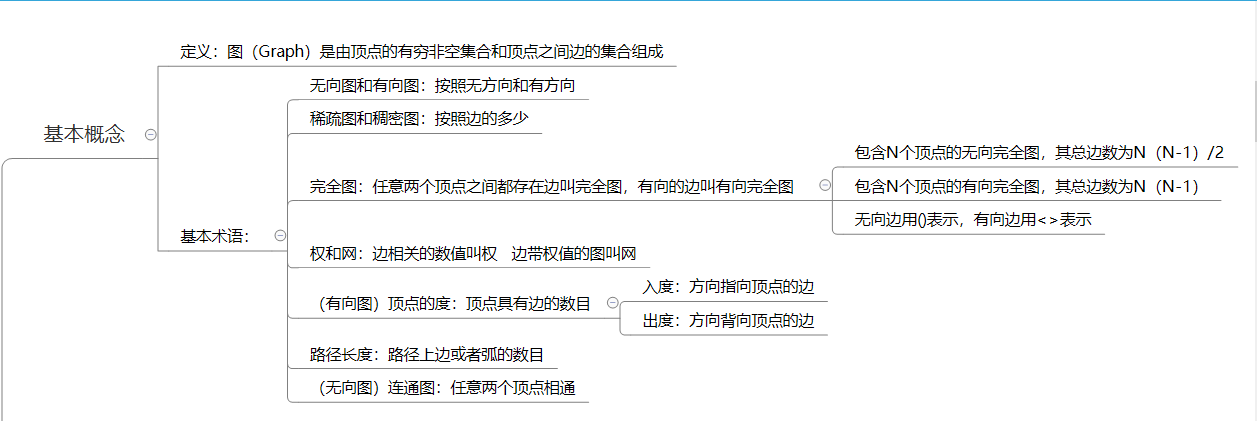
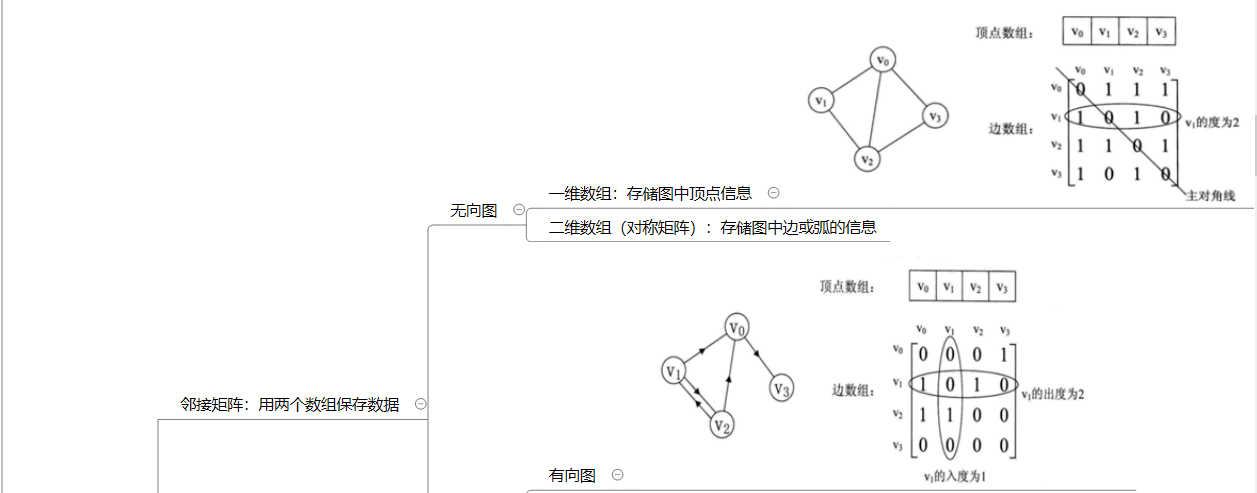


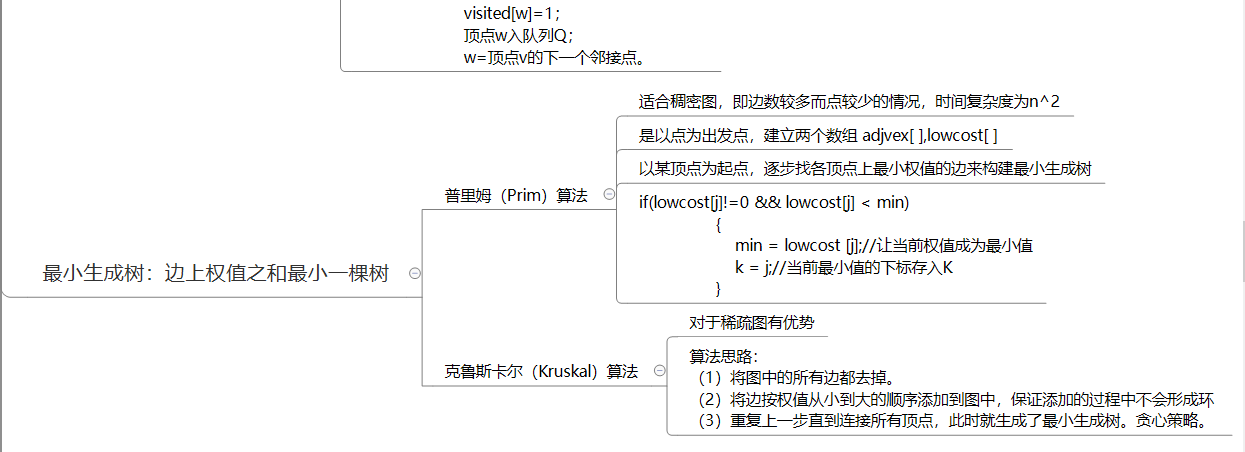



1.2 图结构学习体会
- 深度遍历算法(DFS):一直往深处走,直到找到解或者走不下去为止;类似于树的先序遍历;利用递归(实质上是用栈来保存未访问的结点,先进后出)来实现比较简单;
- 广度遍历算法(BFS):利用队列(用队列来保存未访问的结点,先进先出)实现;类似于树的层次遍历;
- DFS 和 BFS 本质区别:BFS 的重点在于队列,而 DFS 的重点在于递归;
- Prim和Kruscal算法:寻找最小生成树,求最短路径;这两种算法的核心是并查集;一个是选点,一个是选边;当题中边的数目较为复杂时,选用prim算法;一般性问题,选kruscal算法,理解起来比较简单;
- Dijkstra算法:类似于Prim算法,唯一区别为:mindist[ ]的意义变为了原点到其他点的距离;这种算法只能解决权值不是负的图;特点:可以求出单源点到其他顶点的最短距离,算法的复杂程度比floyd算法稍微低一些;
- Floyd算法:时间复杂度比较高,不适合计算大量数据;特点:可以求多源最短路,权值同样不能为负;
- 拓扑排序算法:拓扑排序是针对有向无环图,基于队列来统计入度,先选择输出入度为0的点,删去该点及有关边,再依次循环处理其余点的入度;
- 算法比较多,需要理解并记忆,图比线性表和树更复杂,存储及遍历都需要记住,简单操作如建图、DFS、BFS;
2.PTA实验作业
2.1 题目1:7-1 图着色问题
- 对给定的一种颜色分配,请你判断这是否是图着色问题的一个解;
2.2 设计思路
- void DFS(MGraph g,int v);//深度遍历 void CreateMGraph(MGraph &g,int n,int e );//建图
- 伪代码:
定义变量n、e、k分别是无向图的顶点数、边、颜色数
定义数组 color[MAXV]={0}表顶点颜色并置零
sum 记录当前颜色总数目 ,标记变量 flag=0
数组c[MAXV]表 颜色类型
for i=1 to n
判断着色,不同,sum++
图的遍历:
if(颜色数sum不等于K) 不符合flag=1
else
通过邻接矩阵判断
2.3 代码截图

2.4 PTA提交列表说明

- 部分正确;图不连通,DFS不重复访问顶点的错误,答案错误,图的建立需要顶点初始化,顶点、边数要赋值好;
- 答案错误;有小于K种颜色,题目中颜色数可能恰好相等,需要判断sum!=k;
2.1 题目2:7-3 六度空间
- 假如给你一个社交网络图,请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比;
2.2 设计思路
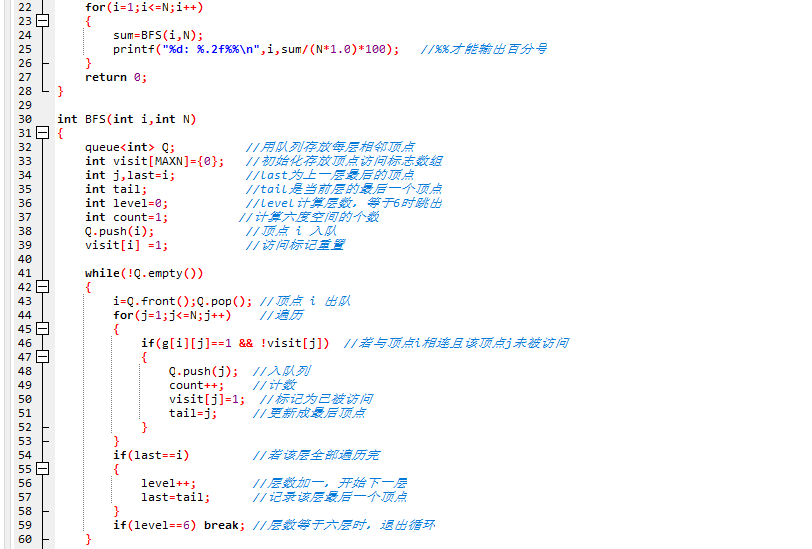
- int g[MAXN][MAXN]; //建图 int BFS(int i,int N); //对图进行广度遍历
- 伪代码:
双精度double sum 记录六度空间总数
queue<int> Q; //用队列存放每层相邻顶点
标志数组 visit[MAXN]={0},层数level=0,tail记录最后顶点
对每个结点进行BFS,获取六度内的结点数sum
for i=1 to N
{
顶点相连且该顶点未被访问,入队,计数
tail 更新
}
一层层BFS,直到 level==6 break
输出: sum/(N*1.0)*100) //%%才能输出百分号
2.3 代码截图
2.4 PTA提交列表说明

- 在DEV-C运行正确后提交无误;
- 过程中错误:图初始化时,节点从1到N编号,图是从0开始的 ;
- 定义一个 last记录当前层访问的最后一个节点 ,查资料所得;%%才能输出百分号 ;
2.1 题目3:7-4 公路村村通
- 现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本;
2.2 设计思路
- int g[MAX][MAX]; //建无向图,以邻接矩阵进行存储 void Prim(int N); //普里姆算法
- 伪代码:
定义数组 lowcost[MAX]存放最低成本
定义变量 min,sum=0
lowcost[1] //序号为1的顶点出发
for i=0 to N-1 //找出N-1个顶点即可
{
min=INF;
for(j=1;j<=N;j++) // 找生成树距离最近的顶点
比min 小 更新
K记录最近顶点
sum=sum+lowcost[k];
}
2.3 代码截图

2.4 PTA提交列表说明


- 段错误;M<N-1,不可能有生成树 ,对一开始的顶点判断,加上条件if(N<=0||M<N-1);
- 答案错误;最大N和M,连通,在Prim()函数里面进行判断,加上if(i<=N) return -1;
- 答案错误;M达到N-1,但是图不连通,判断最小为无穷,则表示不连通, if(min==INF) return -1,前面改的也要变化;
3.截图本周题目集的PTA最后排名
3.1 PTA排名

3.2 我的总分:221
4. 阅读代码
- 二分图匹配——棋盘游戏,题目链接:[https://blog.csdn.net/a1046765624/article/details/79440860]
- 代码:
#include <cstdio>
#include <cstring>
#include <queue>
#include <stack>
#include <vector>
#include <algorithm>
#define MAXN 110
using namespace std;
int G[MAXN][MAXN];
int pipei[MAXN];
bool used[MAXN];
int N, M,K;
void init()
{
memset(G,0,sizeof(G));
}
void getMap()
{
int u,v;
for(int i = 0; i < K; i++)
{
scanf("%d%d",&u,&v);
G[u][v]=1;
}
}
int find(int x)
{
for(int i = 1; i <=M; i++)
{
int y = G[x][i];
if(y&&!used[i])
{
used[i] = true;
if(pipei[i] == -1 || find(pipei[i]))
{
pipei[i] = x;
return 1;
}
}
}
return 0;
}
int solve()
{
int ans = 0;
memset(pipei, -1, sizeof(pipei));
for(int i = 1; i <=N; i++)
{
memset(used, false, sizeof(used));
ans += find(i);
}
return ans;
}
int te=0;
int main()
{
while(~scanf("%d%d%d", &N,&M,&K))
{
te++;
init();
getMap();
int ans=solve();
int su;
int sum=0;
for(int i=1;i<=N;i++)
{
for(int j=1;j<=M;j++)
{
if(G[i][j])
{
G[i][j]=0;
su=solve();
if(su<ans)sum++;
G[i][j]=1;
}
}
}
printf("Board %d have %d important blanks for %d chessmen.
",te,sum,ans);
}
return 0;
}
- 代码思想:二分图匹配,匹配行和列,最后,搜索所有边,每次删除一条边,如果最大匹配变少了,这条边(就是棋盘位置)就是关键位置;
- 本题为二分图应用,有用到匈牙利算法,其本质就是寻找最大流的增广路径,本题中利用匈牙利算法求出最大匹配,即可放置的最大车的数量;
- 还有STL的应用,用STL中的 vector 建立邻接表实现匈牙利算法,效率比较高 ;
- 匈牙利算法有两种版本: DFS 和 BFS ,有利于我们结合所学进行联系比较学习;
- 二分图的最大匹配、完美匹配和匈牙利算法链接:[http://blog.jobbole.com/106084]
5.Git提交
