定义:设G是一个有向图,其中每条边(i, j)都有一个非负的长度L[i, j],若点i 到点j 没有边相连,则设L[i, j] = ∞. 要找出每个顶点到其他所有顶点的最短路径所对应的长度。
如:
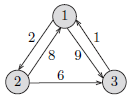
则,L: 0 2 9
8 0 6
1 ∞ 0
运用Floyd-Warshall算法, 时间复杂度为O(n3),空间复杂度为O(n2).
算法基本思路:
引理,点 i 到点 j 的最短路径可能是点 i 到点 j 的直接路径长度,也可能是以某点 k 为中间节点,i, k, j 的路径长度。
采用自底向上逐步求解的方法,设D[i, j, k] 表示 点 i 到 j 以点集[0..k] 为中间节点的最短路径。

k 从0开始枚举各点,则第一步先求所有点以可能经过点0为中间节点的最短路径;
第二步求所有点以可能经过点1为中间节点的最短路径,在此时所有的D[i, j] 已经考虑过0作为中间节点的最短路径,即第二步做的是以点集[0..1]作为考虑,满足自底向上,不难看出,到了最后一步,就是以点集[0...n-1]作为考虑,此时求得的D[i, j] 就是最短路径。
算法具体实现:
输入:L[0...n-1][0...n-1] L[i][j] 表示 i 到 j 的直接路径长度
为了节约空间,可在原来的空间上做自底向上求解,即D只需二维。
首先初始化D[0...n-1][0...n-1],令 D[i][j] = L[i][j],无穷大的数就初始化为一个当前类型的最大值。
然后从0开始迭代k,D[i][j] = min(D[i][j], D[i][k] + D[k][j]),注意可能出现的无穷大值,即i 到 k 没有直接路径或k 到 j 没有直接路径,此时需要做比较,否则相加可能会出现“奇怪”的数字。
代码:

/* input: l[0..n-1][0..n-1] //l[i][j] = the stright length between point i and j table: d[0..n-1][0..n-1] //d[i][j] = the minimum length between point i and j enumerate k, 0<= k <=n-1, d[i][j] = min(l[i][j], d[i][k]+d[k][j]) */ public class Floyd { public static int[][] floyd(int[][] l){ int[][] d = new int[l.length][l.length]; //init d[i][j] = l[i][j] for(int i = 0; i < d.length; i ++){ System.arraycopy(l[i], 0, d[i], 0, d.length); } //compute for(int k = 0; k < d.length; k ++){ for(int i = 0; i < d.length; i ++){ for(int j = 0; j < d.length; j ++){ if(d[i][k] != Integer.MAX_VALUE && d[k][j] != Integer.MAX_VALUE) d[i][j] = Math.min(d[i][j], d[i][k] + d[k][j]); } } } return d; } public static void main(String[] args) { int[][] l = { {0, 7, 1, 6}, {Integer.MAX_VALUE, 0, 9, Integer.MAX_VALUE}, {4, 4, 0, 2}, {1, Integer.MAX_VALUE, Integer.MAX_VALUE, 0} }; int[][] d = floyd(l); for(int i = 0; i < d.length; i ++){ for(int j = 0; j < d[i].length; j ++){ System.out.print(d[i][j] + " "); } System.out.println(); } } }
