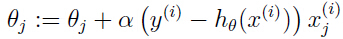首先，我们引入分类问题，其实分类问题和回归问题很相似，只是分类问题中我们要预测的y值是有限数量的离散值，而不是回归问题中的连续值。
为了说明，我们现在只讨论二分类问题，也就是说y只能取0和1两种值。
对于这种二分类问题，当然也可以用线性回归去学习，然后根据给的的x预测出y,只是当预测出的y大于1或者小于0的时候是没有意义的，因为y只能取0或者1.
为了解决这种问题，我们可以提出下面的假设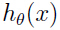
：
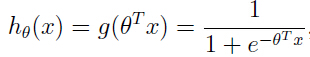
其中
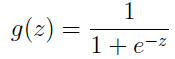
被称之为逻辑函数（logistic function or sigmoid function）,g(z)的函数曲线如下图：
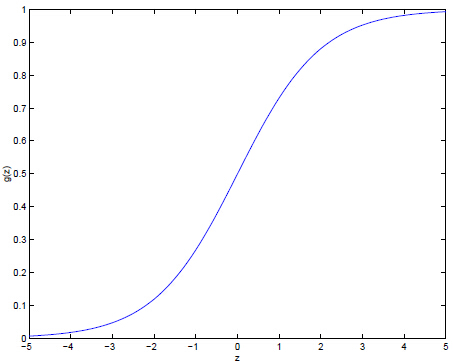
当z趋向正无穷时，g(z)趋向1，当z趋向负无穷时，g(z)趋向0.
因为这种特性，上面我们的假设的值也就被限制在0和1之间。
这就等于给出了逻辑回归的模型，该如何选择参数θ呢？
从概率的角度出发，作出如下假设：
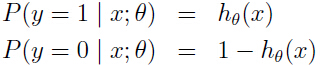
当然这个假设也可简写为：
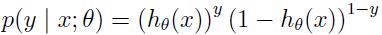
假如每一样本都是互相独立的，就可以得出参数θ的似然函数：
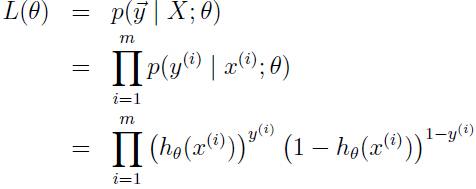
自然得到对数似然函数：
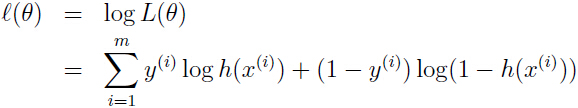
现在就是要最大化这个对数似然函数，和线性回归类似，我们同样可以用梯度下降，关键还是对对数似然函数求导：
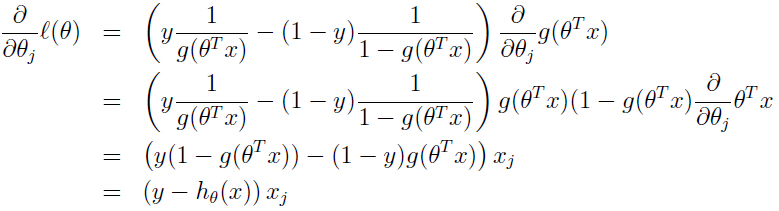
注意上面推导用到了逻辑函数g(z)的一个性质：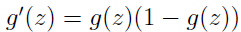
.
因此参数更新可以按照如下规则进行：
