牛顿方法

在

逻辑回归之问题建模分析

中我们提到最大化参数θ的最大化似然函数

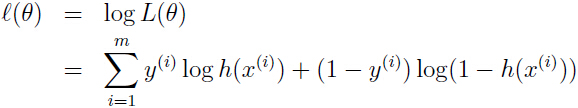
可以用梯度下降法，对参数进行更新直至上面的对数似然函数收敛。下面引入另一种方法：牛顿方法。

开始，首先我们考虑如何找到一个函数的零点。也就是我们有一个函数：，我们希望找到一个值θ，使得.

我们首先随机取某一点(x,f(x))，那么f(x)在该点处的斜率就是f'(x)，根据几何学该点处的斜率同样等于(f(x)-f(θ))/(x-θ);

于是有：f'(x) = (f(x)-f(θ))/(x-θ),又f(θ) = 0我们可以得到：θ = x - f(x) / f'(x);这就是如何由任一点x寻找到θ的公式，很自然的得出在寻找f(x)

零点的时候，参数θ的迭代规则：

下面是牛顿法的执行过程：

由上图可以看出在迭代过程中我们所取得点（红色标注）慢慢靠近零点（θ，0）.

好了，牛顿法给了我们如何找出函数零点的方法，如何用来最大化上面最开始提到的似然函数呢？

根据解析几何，很容易想到，函数的最大点对应着函数的导数为0的点，于是，我们的目标就变为寻找的零点。

也就是说我们让，这样在最大化似然函数的时候，很容易得出参数更新规则：

在逻辑回归中，θ通常是个矢量值，所以对于多维的牛顿法更新规则：

其中是关于θ的偏导数向量，H被称为海森矩阵（Hessian）:

牛顿法收敛速度要比梯度下降快，而且迭代次数要求很小.但是由于每一步都需要计算海森矩阵的逆，所以当维数太大时，就不太划算。即当变量维数不是很大的时候，

牛顿法的速度通常会比较快。

 具体matlba操作，参考我的博客：逻辑回归实战。