考虑一个多分类问题，即预测变量y可以取k个离散值中的任何一个.比如一个邮件分类系统将邮件分为私人邮件，工作邮件和垃圾邮件。由于y仍然是一个离散值，只是相对于二分类的逻辑回归多了一些类别。下面将根据多项式分布建模。
考虑将样本共有k类，每一类的概率分别为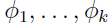
,由于
，所以通常我们只需要k-1个参数
即可
，
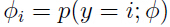为了推导，引入表达式：
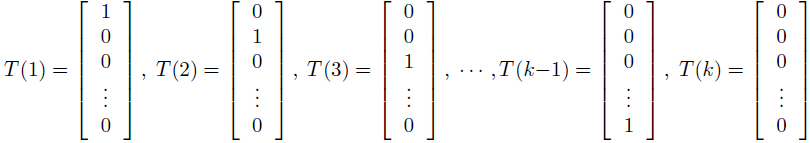
上面T(y)是k-1维列向量,其中y = 1, 2, ...k.
T(y)i 表示向量T(y)的第i个元素。
还要引入表达式 
,如果大括号里面为真，则真个表达式就为1，否则为0.例如：1{2=3} = 0和1{3=3} = 1.
则上面的k个向量就可以表示为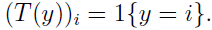
以为y只能属于某一个类别，于是T(y)中只能有一个元素为1其他元素都为0，可以求出k-1个元素的期望：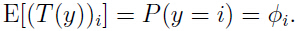
定义：
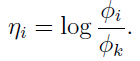
其中i = 1,2,...k.
则有：
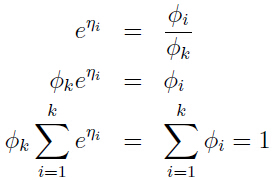
也就容易得出：
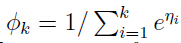，由该式和上面使得等式：
一起可以得到：
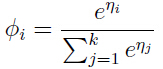
这个函数就是softmax函数。
然后假设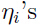
和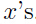
具有线性关系，即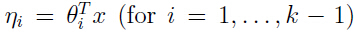
于是从概率的角度出发：
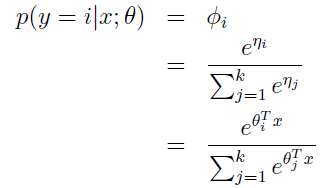
其中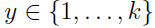
这个模型就是softmax回归（softmax regression）, 它是逻辑回归的泛化。
这样我们的输出：
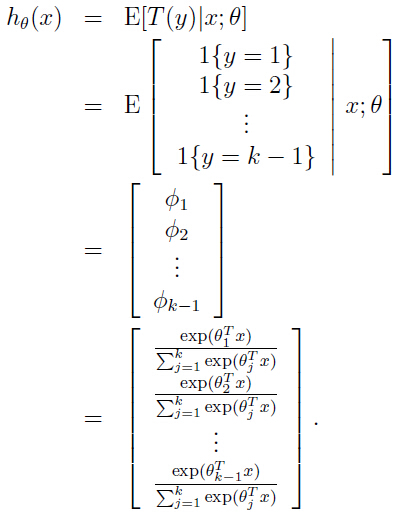
就是输出了x属于（1,2,...k-1）中每一类的概率，当然属于第k类的概率就是：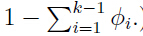
下面开始拟合参数
同样使用最大化参数θ的对数似然函数：
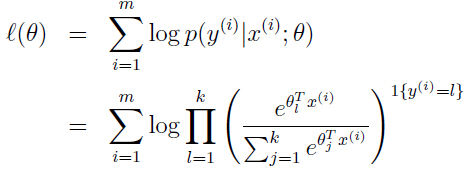
这里使用梯度下降和牛顿法均可。