第一种查找方法:也是我们经常用的查找方法。
/*确实伪代码很难看,但是还是要训练。*/
int SequentialSearch(statictable *Tbl,ElementType k) { /*在表Tbl[1]~Tbl[n]中查找关键字为K的数据元素*/ int i; Tbl->Element[0]=k//建立哨兵(后面应该有大用处吧。这里了解一下!) for(i=Tbl->Length;Tbl->Element[i]!=k;i--)
; return i;/*查找成功的话返回单元下标,不成功的话返回0*/ }
这个时间复杂度为O(n)很差劲的时间复杂度。 下面带上二分查找瞪大眼睛。
二分查找(数学上咱们应该就有所了解了)
然后联想了一下,,,发现不现实,为什么呢? 从中间看 怎样知道 要查找的数字在哪一边?
所以要求数字要按序存放。
/*二分查找, 对应的时间复杂度为 O(logN) 很小的时间复杂度 */ int binarysearch(StaticTable *Tbl,ElementType k) { int left,right,mid,NoFound=-1; left=1; // 初始化 左边界 right=Tbl->length //初始化 右边界 while(left<=right) { mid=(left+rigth)/2; //计算中间的坐标。 if(k<Tbl->Element[mid]) right=mid-1; //调整右边界。 else if(k>Tbl->Element[mid]) left=mid+1; //调整左边界 else return mid; //查找成功 返回位置。 } return NotFound; //查找不成功。 /*查找的数字里面没有*/ }
层次化的储存数据类似于上面的二叉树,插入数据删除数据也十分的方便。并且可以高效的找到某一个元素
所以 二叉树 应该在以后的工作中很重要。下面附上图示
树:n(n>=0)个节点构成的有限集合。
当n=0时,称为空树;
对于任意一颗非空树(n>0)它具备如下性质。
♢ 树中有一个称为“根(root)”的特殊节点,用r来表示。
♢ 其中即诶但又可以分为m(m>0)个互不相交的有限集T1,T2,`````Tm,其中每个集合本身又是一个数,称为原来的树的子树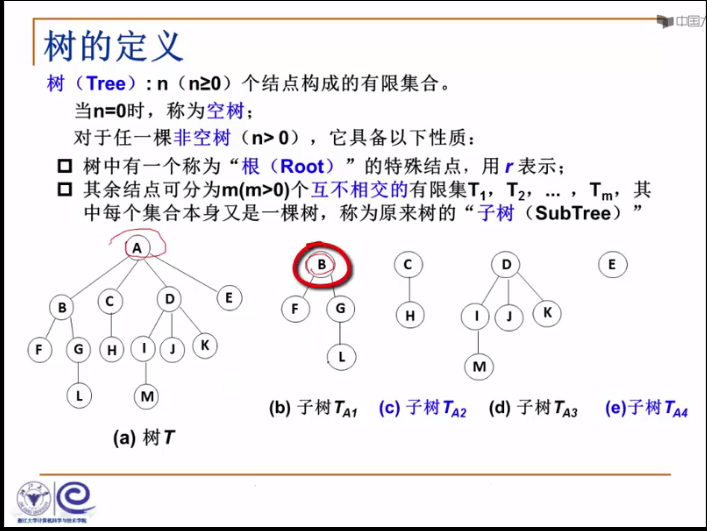
切记树是不相交的。
树有n条边就有n-1个节点。
-------------------------树的一些术语------免得到时候说话丢人-----看看吧,----------
1:节点的度(degree):结点的子树个数(建议外国人发明的东西看外国人的注释或者明明是最容易理解的)
2:树的度 :树的所有节点中最大的度数。
3:叶结点(leaf) :度为0的节点(没有分叉就是叶子)
4:父结点 (parent) :有子树的结点是其子树节点的父节点.
5:子节点(child) :若A节点是B 节点的父节点则B节点是A节点的子节点。
6:兄弟节点(sibling) :具有同一父节点的各个节点彼此是兄弟节点。
7:路径和路径长度 :从节点n1到节点nk的路径为一个节点的序列n1,n2,n3。。。。nk,Nj是Nj+1的父节点。路径所包含的边的个数称为路径的长度。
8:祖先节点(Ancestor):沿着树根到某一节点路径上所有节点是这个节点的子孙。
11:节点的层次(level) :规定根节点在第一层其他任一节点的层数是其父节点的层数+1.
12:树的深度(depth) :树中所有节点的最大层次是这棵树的深度
-------------------------数的表示-------------------------
1:数组很明显不能表示这种关系,所以自然的就想到了链表。
 儿子兄弟表示法左手儿子右手拉着兄弟这样一个节点就只用两个指针域就行。省时又省力。
儿子兄弟表示法左手儿子右手拉着兄弟这样一个节点就只用两个指针域就行。省时又省力。 传说中的二叉树。
传说中的二叉树。