--------二叉搜索树-----

二叉搜索树（BST，Binary Search Tree）---

♢　　静态查找和动态查找（下一节会讲）

♦　　针对查找，数据如何组织？

为什么在前面咱们说的二分查找的效率会那么高？这是因为在查找之前我们就对数据进行了有效的组织。

这时候估计有人该有疑问了，咱们说了这么多数据结构但是好像都有很大的限制，例如这个搜索，就需要事先对数据有效的组织那么输入的时候岂不是很麻烦？这样太耗费人力了。如果你能这样想的话很幸运，你是一个实干主义者，程序设计就需要实干主义者个。但是这也反馈出来一个很严重的问题，你的程序思维不重，为什么你没有想到 我们只管输入至于有序的组织在我们输入的时候让程序自动的去有序的组织呢?

-----x下面就开始说如何让程序有效的组织输入------

对前面在以为数组中的二分查找进行联想，---------我们可以得出一种方法，我们可以对根节点来说我们让其左子树的所有值都比根节点要小，右子树的所有值都别根节点的要大（所有的节点都可以作为根节点）。  质疑一下  能完成么？  怎样去完成？（思考①）

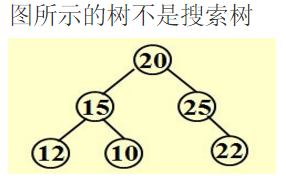
二叉搜索树的基本操作：

　　Position Find（ElementType X，BinTree  BST）：从二叉搜索树树BST中查找元素X，返回其所在的节点的地址；

　　Position FindMin（BinTree BST）：从二叉搜索树BST中查找并返回最小元素所在的节点。

　　Position FindMax（BinTree BST）：

----------------二叉树查找操作的尾递归实现方法----------------------------

Position Find(ElementTYpe X,BinTree BST)    //需要查找X，在 BST之中。
{
    if(!BST)              //    判断 树是否为空。
        return NULL;         //
    if(x>BST->Date)              //如果比根节点 大的话
        return Find(X,BST->Right);   //转向根节点的右边    
    else
        if(x<BST->Date)
        return Find(X,BST->Left);
    else
        return BST;  //不大也不小的时候刚好就   查找到了。如果查找完了，但也没找到，，那就在最上面返回NULL了。
}

所有的尾递归在理论上都可以转化为循环来实现。（自己想想为啥，遇事多思考！）

/*太简单  不做注释*/
Position IterFind(ElementType X,BinTree BST)
{
    while(!BST)
    {
        if(X>BST->Date)
            BST=BST->Right;
        else
            if(X<BST->Date)
            BST==BST->Left;
        else
            return BST;
    }
    return NULL;
        
}

咱们可以看到查找的效率决定于树的高度（对于循环程序来说是，循环的次数）那么如果我们想让程序的时间复杂度尽可能的低，就要想办法来让树长的粗壮而不是瘦高。（留作思考）

下面我们来说一下最大值，和最小值得寻找。（如果你思考①认真的做了的话，你就会明白程序的思路）。

Position FindMin(BinTree BST)
{
    if(!BST)
    return NULL;
    while(!BST)  //如果没有查找到树的低端的时候 就继续
    {
        BST=BST->Right;
    }
    return BST;
}

最小的自己想。

-----------------------------下面开始说二叉树的插入---我感觉二叉树的插入完全可以作为输入信息时的---自动规律化输入------

先找一个  中值作为根节点，然后开始做所谓的插入程序。

BinTree Insert(ElementType X,BinTree BST)
{
    if(!BSt)   //原先没有树的话
    {
        BST=(******)malloc(sizeof(struct TreeNode));//声明一棵树 ，取长度，开辟空间,然后转化成你需要的类型
        BST->Date=X;
        BST->Left=BST->Right=NULL;
    }    
    else
    while(1)           //没有考虑相同元素的情况。
    {
        if(X<BST->Date)
            BST=BST->left;
        else
            if(X>BST->Right)
            BST=BST->Right;
        if(!BST)
        {
            BST=(******)malloc(sizeof(struct TreeNode));
            BST->Date=X;
            break;
        }
    }
}

下面是十二个月的查找树（按照字典序比大小）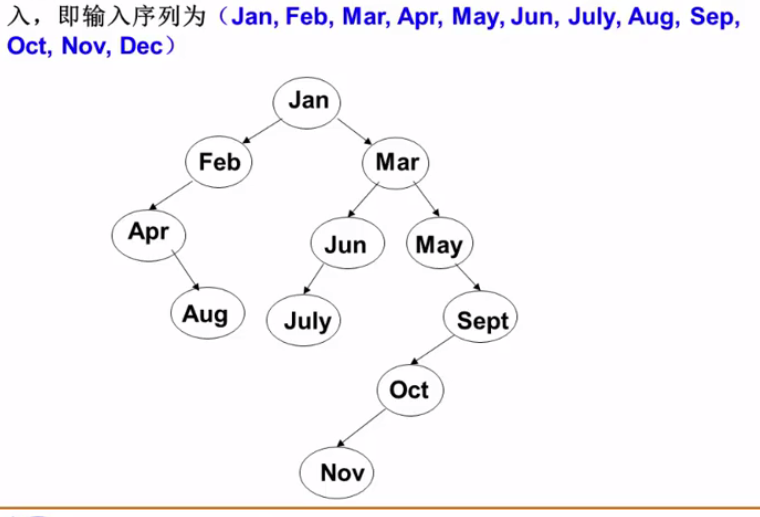

 ------------------------下面是二叉树的删除--------------------------------（再次理解思考①）

叶子节点，和一个儿子的节点容易删除，下面直接看有两个儿子节点的删除操作。

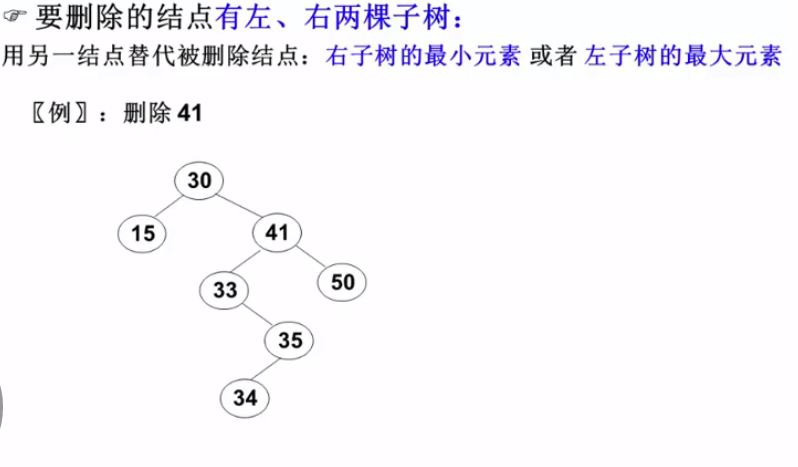
想删除41，怎么办呢？    那句话杂说来 ，，，简单的问题堆起来就很复杂，复杂的问题拆分了就很简单，思考一下能不能将他转化一下。

思考了但是发现不能将他转换成  叶子，或者一个儿子。。。。。。。还有一句话咋说的，只要想就没有做不成的事。  

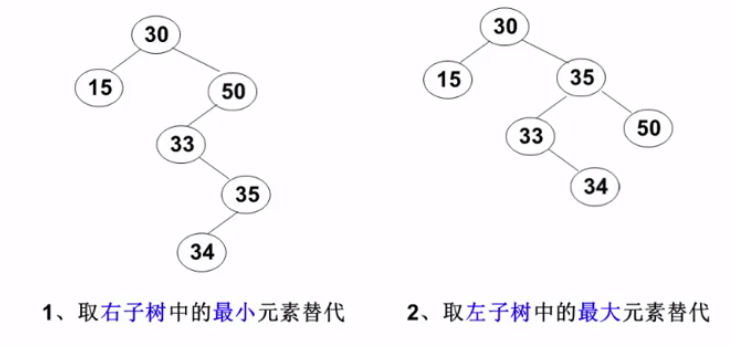
最小最大的元素一定是  子叶。。。（思考①）。

------------------代码出来吧！--------------------------

BinTree Delete(ElementType X,BinTree BST)
{
    PosiTion Tmp；
    if(!BST)
        printf("没有找到你所需要的元素
");
    else
        while(1)           //没有考虑相同元素的情况。
    {
        if(X<BST->Date)
            BST=BST->left;
        else
            if(X>BST->Date)
            BST=BST->Right;
        else  //不大不小   找到了。
        if(BST->Right&&BST->Left)  //需要删除的节点有两个儿子。
        {
            Tmp=BST;//先用一个临时变量储存起来需要删除的节点。
            Tmp=TMP->Rigth;
            while(!Tmp)//  开始在该根节点的右子树那里寻找 最小值
            {
                Tmp=TMP->Left;    //要出去的时候  BST就是左子树中最小的节点
            }
            BST->Date=Tmp->Date;
            BST->Right=Delete(BST->Datem,BST->Right);//调用本函数，去解决 被复制的节点。
        }
        else
            {
                if(!BST->Left)
                    BST=BST->Right;
                else
                if(!BST->Right)
                BST=BST->Left;
        
            }
    }
    return BST;
        
}