PAT 1131 Subway Map

In the big cities, the subway systems always look so complex to the visitors. To give you some sense, the following figure shows the map of Beijing subway. Now you are supposed to help people with your computer skills! Given the starting position of your user, your task is to find the quickest way to his/her destination.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤ 100), the number of subway lines. Then N lines follow, with the i-th (i=1,⋯,N) line describes the i-th subway line in the format:

M S[1] S[2] ... S[M]

where M (≤ 100) is the number of stops, and S[i]'s (i=1,⋯,M) are the indices of the stations (the indices are 4-digit numbers from 0000 to 9999) along the line. It is guaranteed that the stations are given in the correct order -- that is, the train travels between S[i] and S[i+1] (i=1,⋯,M−1) without any stop.

Note: It is possible to have loops, but not self-loop (no train starts from S and stops at S without passing through another station). Each station interval belongs to a unique subway line. Although the lines may cross each other at some stations (so called "transfer stations"), no station can be the conjunction of more than 5 lines.

After the description of the subway, another positive integer K (≤ 10) is given. Then K lines follow, each gives a query from your user: the two indices as the starting station and the destination, respectively.

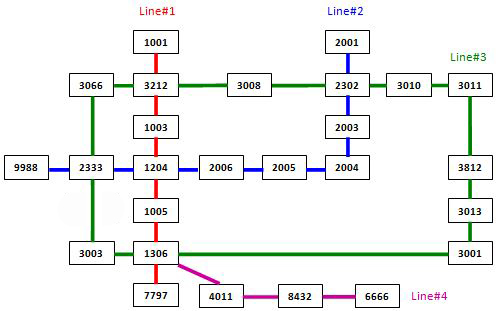
The following figure shows the sample map.

Note: It is guaranteed that all the stations are reachable, and all the queries consist of legal station numbers.

Output Specification:

For each query, first print in a line the minimum number of stops. Then you are supposed to show the optimal path in a friendly format as the following:

Take Line#X1 from S1 to S2.
Take Line#X2 from S2 to S3.
......

where Xi's are the line numbers and Si's are the station indices. Note: Besides the starting and ending stations, only the transfer stations shall be printed.

If the quickest path is not unique, output the one with the minimum number of transfers, which is guaranteed to be unique.

Sample Input:

4
7 1001 3212 1003 1204 1005 1306 7797
9 9988 2333 1204 2006 2005 2004 2003 2302 2001
13 3011 3812 3013 3001 1306 3003 2333 3066 3212 3008 2302 3010 3011
4 6666 8432 4011 1306
3
3011 3013
6666 2001
2004 3001

Sample Output:

2
Take Line#3 from 3011 to 3013.
10
Take Line#4 from 6666 to 1306.
Take Line#3 from 1306 to 2302.
Take Line#2 from 2302 to 2001.
6
Take Line#2 from 2004 to 1204.
Take Line#1 from 1204 to 1306.
Take Line#3 from 1306 to 3001.

分析
参考最短路径解析

#include<iostream> //偏难，使用dfs来找寻无权图的最短路径
#include<vector>
#include<unordered_map>
using namespace std;
int start, end1, mincnt=99999, mintransfer=99999;
unordered_map<int, int> line;
vector<vector<int>> graph(10000); 
vector<int> visited(10000, 0), temppath, ans;
int transfercnt(vector<int> a){
	int preline=0, cnt=0;
	for(int i=1; i<a.size(); i++)
		if(line[a[i-1]*10000+a[i]]!=preline){
			cnt++;
			preline=line[a[i-1]*10000+a[i]];
		}
	return cnt;
}
void dfs(int node, int cnt){
	if(node==end1&&((cnt<mincnt)||((cnt==mincnt)&&(transfercnt(temppath))<mintransfer))){
		ans=temppath;
		mincnt=cnt;
		mintransfer=transfercnt(temppath);
	}
	if(node==end1) return;
	for(int i=0; i<graph[node].size(); i++){
		if(visited[graph[node][i]]==0){
			visited[graph[node][i]]=1;
			temppath.push_back(graph[node][i]);
			dfs(graph[node][i], cnt+1);
			temppath.pop_back();
			visited[graph[node][i]]=0;
		}
	}		
}
int main(){
	int n, temp;
	cin>>n;
	for(int i=1; i<=n; i++){
		int sn, pre;
		cin>>sn>>pre;
		for(int j=1; j<sn; j++){
			cin>>temp;
			graph[temp].push_back(pre);
			graph[pre].push_back(temp);
			line[pre*10000+temp]=line[temp*10000+pre]=i;
			pre=temp;
		}
	}
	cin>>n;
	for(int i=0; i<n; i++){
		cin>>start>>end1;
		mincnt=mintransfer=99999;
		temppath.clear();
		temppath.push_back(start);
		visited[start]=1;
		dfs(start, 0);
		visited[start]=0;
		cout<<mincnt<<endl;
		int preline=0, pretransfer=start;
		for(int j=1; j<ans.size(); j++){
			if(line[ans[j-1]*10000+ans[j]]!=preline){
				if(preline!=0)
					printf("Take Line#%d from %04d to %04d.
", preline, pretransfer, ans[j-1]);
				preline = line[ans[j-1]*10000+ans[j]];
                pretransfer = ans[j-1];	 
			}
		}
		printf("Take Line#%d from %04d to %04d.
", preline, pretransfer, end1);
	}
	return 0;
}