Kruskal重构树
前置知识:Kruskal算法, LCA
最近刚学,如有错误欢迎提出。
对图建Kruskal重构树的主要作用:求原图中两个点所在路径上的最长边的最小值或最短边的最大值。
如何建Kruskal重构树
在Kruskal的基础上,当两个点x, y 不再一个并查集中,那么我们就再引入一个新的点,这个点的权值是x,y两点再原图中的边的权值。最后把两个并查集的根节点指向新的点。
(下图中右边是左边图建立的Kruskal重构树)
- 首先是连4和6两个点,引入一个新点7,连边4和7以及6和7,其权值是2
- 然后连3和4这一条边,引入一个新点8,连3和4所在的并查集的根节点7,权值为3.
- 后面和前面一样,和kruskal算法过程差不多。
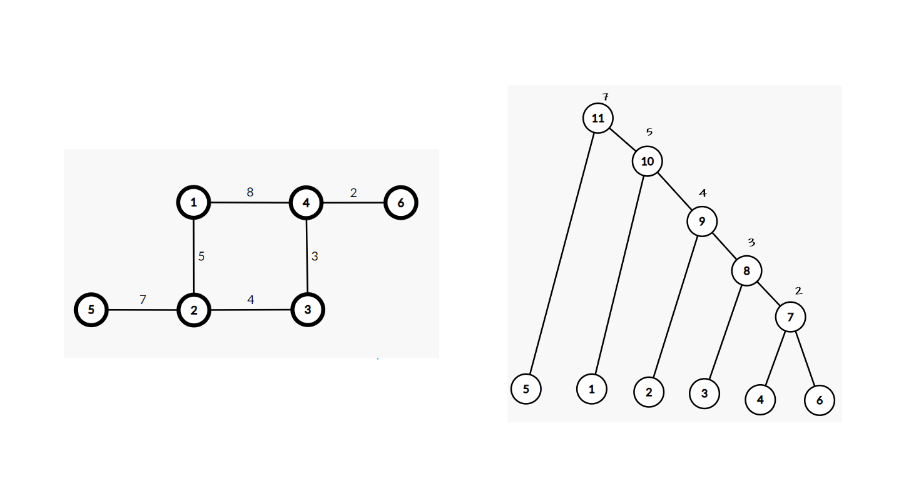
为什么能算出来呢?
首先如果要求两点路径最长边的最小值。我们需要按照边权从小到大去建kruskal重构树,注意所有新点表示的其实是一条边,这时只有x, y两点lca这个点连边x和y才能联通,那么才能有一条路径使x,y相连,由于从小到大连边,那么最后连的lca表示的这条边一定是路径中的最大边,
又因为后面连的边都比lca表示的边大,后面出现的x,y之间的边的最大值一定比lca这条边大,所以lca点表示的边是x,y之间路径的最大边的最小的那一条。
求两点之间路径最小边的最大值思路一样,不过是从大到小建kruskal重构树。
代码实现:
代码其实很清楚,看别的博客把lca和建树写在一起了,这样虽然很好写,但是我感觉会让新学习的人看到各种命名的数组很懵。所以我分开了。
建树:
//add(u,v)是建链式前向星图
//Find(x)是找x并查集根节点,root[x]表示x所在并查集根节点
//e[i]存原图,排序后建kruskal重构树
//tot表示新点,初值为n
for(int i = 1; i <= m; ++ i){
int x = e[i].u, y = e[i].v; ll z = e[i].w;
int tx = Find(x), ty = Find(y);
if(tx == ty) continue;
root[tx] = root[ty] = ++ tot; //把两个并查集根指向新的点
val[tot] = z; //新点的权值是新连边的边权
add(tot, tx); add(tot, ty); //建重构树,把新点和两个并查集根连边
}
是的,上面就建好kurskal重构树了。和求kruskal算法过程简直很像。
下面是求LCA,用自己板子就行了。
//f[i][j]表示从i点向上2^j步的点
void bfs(){
q.push(tot);
dep[tot] = 1;
while(!q.empty()){
int u = q.front();
q.pop();
for(int i = head[u]; i != -1; i = nxt[i]){
int v = to[i];
if(dep[v]) continue;
dep[v] = dep[u] + 1;
f[v][0] = u;
for(int j = 1; j <= t; ++ j)
f[v][j] = f[f[v][j - 1]][j - 1];
q.push(v);
}
}
}
int Lca(int x, int y){
if(dep[x] > dep[y]) swap(x, y);
for(int i = t; i >= 0; -- i)
if(dep[f[y][i]] >= dep[x]) y = f[y][i];
if(x == y) return x;
for(int i = t; i >= 0; -- i)
if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
return f[x][0];
}
查询两点x,y之间路径最大边的最小值。
while(Q --){
int x, y; scanf("%d%d",&x,&y);
int lca = Lca(x, y);
printf("%lld
",val[lca]);
}
完整代码:(bzoj 3732 Network)
由于bzoj好像没了,所以代码没交过
更新:交到darkbzoj上过了。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<map>
#include<queue>
#include<vector>
#include<string>
#include<bitset>
#include<fstream>
using namespace std;
#define rep(i, a, n) for(int i = a; i <= n; ++ i);
#define per(i, a, n) for(int i = n; i >= a; -- i);
typedef long long ll;
typedef pair<ll,int> PII;
const int N = 2e6 + 105;
const int mod = 1e9 + 7;
const double Pi = acos(- 1.0);
const ll INF = 1e18;
const int G = 3, Gi = 332748118;
ll qpow(ll a, ll b) { ll res = 1; while(b){ if(b & 1) res = (res * a) % mod; a = (a * a) % mod; b >>= 1;} return res; }
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
// bool cmp(int a, int b){return a > b;}
//
int n, m, Q, t;
int head[N], cnt = 0, tot;
int to[N << 1], nxt[N << 1]; ll c[N << 1];
int root[N << 1];
int f[N][20];
int dep[N];
queue<int> q;
ll val[N];
void add(int u, int v){
to[cnt] = v, nxt[cnt] = head[u], head[u] = cnt ++;
to[cnt] = u, nxt[cnt] = head[v], head[v] = cnt ++;
}
int Find(int x){
return x == root[x] ? x : root[x] = Find(root[x]);
}
struct node{
int u, v; ll w;
bool operator < (const node &a) const {return w < a.w;}
}e[N << 1];
void bfs(){
q.push(tot);
dep[tot] = 1;
while(!q.empty()){
int u = q.front();
q.pop();
for(int i = head[u]; i != -1; i = nxt[i]){
int v = to[i];
if(dep[v]) continue;
dep[v] = dep[u] + 1;
f[v][0] = u;
for(int j = 1; j <= t; ++ j)
f[v][j] = f[f[v][j - 1]][j - 1];
q.push(v);
}
}
}
int Lca(int x, int y){
if(dep[x] > dep[y]) swap(x, y);
for(int i = t; i >= 0; -- i)
if(dep[f[y][i]] >= dep[x]) y = f[y][i];
if(x == y) return x;
for(int i = t; i >= 0; -- i)
if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
return f[x][0];
}
int main()
{
scanf("%d%d%d",&n,&m,&Q);
cnt = 0; tot= n;
for(int i = 0; i <= n * 2 + 1; ++ i){
root[i] = i;
head[i] = -1;
}
for(int i = 1; i <= m; ++ i){
int x, y; ll z; scanf("%d%d%lld",&x,&y,&z);
e[i] = (node){x, y, z};
}
sort(e + 1, e + m + 1);
for(int i = 1; i <= m; ++ i){
int x = e[i].u, y = e[i].v; ll z = e[i].w;
int tx = Find(x), ty = Find(y);
if(tx == ty) continue;
root[tx] = root[ty] = ++ tot;
val[tot] = z;
add(tot, tx); add(tot, ty);
}
t = (int)(log(n) / log(2)) + 1;
bfs();
while(Q --){
int x, y; scanf("%d%d",&x,&y);
int lca = Lca(x, y);
printf("%lld
",val[lca]);
}
return 0;
}