二叉树的遍历及例题
前序遍历就是根在前,中序是根在根在中,
前序遍历
根 --> 左 --> 右
中序遍历
左 --> 根 --> 右
后序遍历
左 --> 右 --> 根
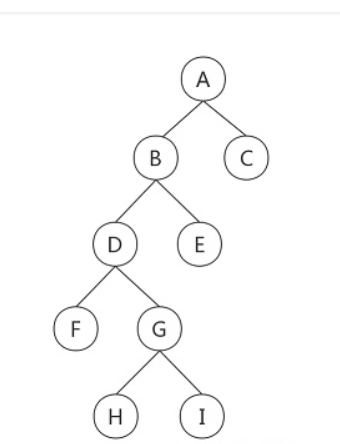
如图是一颗二叉树
前序(根左右),中序(左根右),后序(左右根)
它的前序遍历结果为: A B D F G H I E C 代表的含义为A( B ( D ( F ,G( H ,I ) ) ,E ) , C )
所以第一个点一定是根节点
它的中序遍历结果为: F D H G I B E A C
它代表的含义,A(已知它不是叶子节点)在中间说明A的左边是左儿子,A的右边是他的右儿子
它的后序遍历结果为:F H I G D E B C A
解题:
如果有前序和中序或者中序和后序可以得到二叉树,从而得到后序。
如果有前序和后序无法的得到二叉树。
1.已知前序、中序遍历求后序遍历
例:
前序遍历:A B G D E C F H
中序遍历:G B E D A F C H
构建二叉树的步骤:
1.根据前序遍历特点,得到根节点A
2.观察中序遍历结果: 根节点左边节点为G B E D,根节点的右边节点为 F C H。同时,两段也是左右子树的中序遍历的结果。
B G D E也是左子树前序遍历的结果。 C F H也是右子树前序遍历的结果。
3.重复 1 2的步骤,直到找到叶子结点就可以得到最后的二叉树。
例题:
https://vjudge.net/contest/407936#problem/K
题意:给出中序遍历和前序遍历,让你找到后序遍历的结果。
#include <iostream>
using namespace std;
const int maxn = 105;
int pre[maxn],in[maxn],pos[maxn];
int infind(int root,int l,int r){//在中序遍历中找到当前根节点的位置
for(int i=l;i<r;i++){
if(in[i]==root){
return i;
}
}
}
int cnt;
void posorder(int prel,int prer,int inl,int inr){
if(prel==prer) return ;
int root=infind(pre[prel],inl,inr);//找当前的根的位置
int len=root-inl;
posorder(prel+1,prel+1+len,inl,inl+len);//prel的位置是root的位置,删去
posorder(prel+1+len,prer,inl+1+len,inr);//inl+len+1的位置是root的位置,删去
//进行完左边和右边的遍历之后,进行赋值。 左右根
pos[cnt++]=in[root];
return;
}
int main(){
int n;
while(~scanf("%d",&n)){
cnt=0;
for(int i=0;i<n;i++) cin>>in[i];
for(int i=0;i<n;i++) cin>>pre[i];
posorder(0,n,0,n);
for(int i=0;i<n;i++) cout<<pos[i]<<' ';
cout<<endl;
}
return 0;
}
//关键代码:
void posorder(int prel,int prer,int inl,int inr){
if(prel==prer) return ;
int root=infind(pre[prel],inl,inr);//找当前的根的位置
int len=root-inl;
posorder(prel+1,prel+1+len,inl,inl+len);
posorder(prel+1+len,prer,inl+1+len,inr);
pos[cnt++]=in[root];//相当于输出操作
return;
}
//得到前序遍历的值
pos[cnt++]=in[root];//相当于输出操作
posorder(prel+1,prel+1+len,inl,inl+len);
posorder(prel+1+len,prer,inl+1+len,inr);
//得到中序遍历的值
posorder(prel+1,prel+1+len,inl,inl+len);
pos[cnt++]=in[root];//相当于输出操作
posorder(prel+1+len,prer,inl+1+len,inr);
//得到后序遍历的值
posorder(prel+1,prel+1+len,inl,inl+len);
pos[cnt++]=in[root];//相当于输出操作
posorder(prel+1+len,prer,inl+1+len,inr);
例题:
玩转二叉树
https://pintia.cn/problem-sets/994805046380707840/problems/994805065406070784
题意:给你中序遍历和前序遍历的结果,让你找到二叉树的镜像,然后按层遍历输出
#include <iostream>
using namespace std;
int pre[55],in[55],pos[55];
int ans[55][55];//储存按层遍历的结果
//第一个存的哪一层,第二个存的是具体的数,
//ans[t][0]存储的是该层的数字个数。
int find(int t,int l,int r){
for(int i=l;i<r;i++){
if(in[i]==t){
return i;
}
}
}
void ceng(int prel,int prer,int inl,int inr,int t){
if(prel==prer) return ;
ans[t][++ans[t][0]]=pre[prel];//存入答案。
int x=find(pre[prel],inl,inr);
int len=x-inl;
ceng(prel+len+1,prer,inl+len+1,inr,t+1);//先遍历右边,再遍历左边
ceng(prel+1,prel+len+1,inl,inl+len,t+1);
return;
}
int main(){
int n;
cin>>n;
for(int i=0;i<n;i++) cin>>in[i];
for(int i=0;i<n;i++) cin>>pre[i];
ceng(0,n,0,n,0);
int x=0;
int len=0;
while(ans[x][0]!=0){
for(int i=1;i<=ans[x][0];i++){
if(len==0){
printf("%d",ans[x][i]);
}else{
printf(" %d",ans[x][i]);
}
len++;
}
x++;
}
return 0;
}
2.已知后序、中序遍历求前序遍历
后序遍历是:左右根,所以根在最后,跟前序遍历相似,把 prel 和 prer 的值改变一下即可。
3.已知前序、后序遍历求中序遍历
无法求得!!!