[BZOJ]1018 堵塞的交通(SHOI2008)

　　一道有点神的线段树。

Description

　　有一天，由于某种穿越现象作用，你来到了传说中的小人国。小人国的布局非常奇特，整个国家的交通系统可以被看成是一个2行C列的矩形网格，网格上的每个点代表一个城市，相邻的城市之间有一条道路，所以总共有2C个城市和3C-2条道路。 小人国的交通状况非常槽糕。有的时候由于交通堵塞，两座城市之间的道路会变得不连通，直到拥堵解决，道路才会恢复畅通。初来乍到的你决心毛遂自荐到交通部某份差事，部长听说你来自一个科技高度发达的世界，喜出望外地要求你编写一个查询应答系统，以挽救已经病入膏肓的小人国交通系统。 小人国的交通部将提供一些交通信息给你，你的任务是根据当前的交通情况回答查询的问题。交通信息可以分为以下几种格式：
　　Close r1 c1 r2 c2：相邻的两座城市(r1,c1)和(r2,c2)之间的道路被堵塞了；
　　Open r1 c1 r2 c2：相邻的两座城市(r1,c1)和(r2,c2)之间的道路被疏通了；
　　Ask r1 c1 r2 c2：询问城市(r1,c1)和(r2,c2)是否连通。如果存在一条路径使得这两条城市连通，则返回Y，否则返回N。

Input

　　第一行只有一个整数C，表示网格的列数。接下来若干行，每行为一条交通信息，以单独的一行“Exit”作为结束。我们假设在一开始所有的道路都是堵塞的。

Output

　　对于每个查询，输出一个“Y”或“N”。

Sample Input

　　2
　　Open 1 1 1 2
　　Open 1 2 2 2
　　Ask 1 1 2 2
　　Ask 2 1 2 2
　　Exit

Sample Output

　　Y
　　N

HINT

　　C,信息条数<=100000。

Solution

　　修改、询问……首先确定这是一道数据结构题。

　　可是它每次询问的是两个点的连通性，可持久化并查集？你在逗我？

　　连通性怎么维护？

　　我们发现它实质上是在一条线段上进行连通性维护的，即使它有两条，实际上是没有太大区别的。

　　我们仔细思考一下行数只有1的时候，用数据结构怎么做：

　　用线段树维护只在该区间影响下，区间两端是否连通，合并起来是毫无压力的。

　　那么行数为2的时候，我们也试试看这样维护？

　　我们用线段树维护只在该区间影响下，区间中左上和右上右下，左下和右上右下是否连通，合并起来同样也是没有压力的。

　　这样我们似乎就解决了询问的问题？

　　显然这只是其中一种情况，但是还可能有区间外的边影响其连通性的情况：

　　　　

　　　　

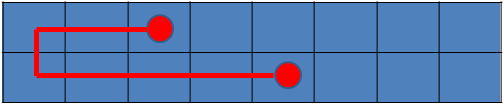
　　当然还有更骚的，可以这样：

　　　　

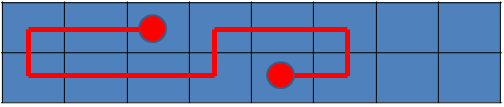
　　其实不外乎就是这4种情况，幸好我们都是可以处理的。

　　你会发现后3种情况我们可以是看作几个区间的共同作用：

　　　　

　　　　

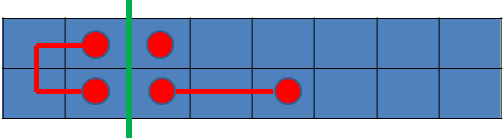
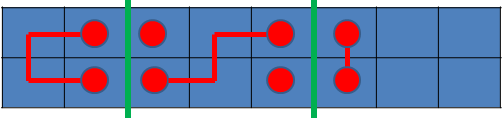
　　这样你就突然发现，每个区间的作用是独立的，也就是说正好是我们所能够维护的。

　　所以除了上面4项需要维护，我们还需要维护区间左上和左下是否连通，右上和右下是否连通，合并同样很好实现。

　　这样我们就完美解决了询问操作。

　　至于修改操作根本就是小case了，小C也大约说一下自己的做法。

　　更改不同行之间的连通性就是直接改。

　　然而更改不同列之间的连通性可以动动脑子，我们可以预处理出第i列到第i+1列之间的道路哪个区间更新时会用到它。

　　例如n=8，第4、5列之间的道路在[1,8]区间更新时被用到；第1、2列之间的道路在[1,2]区间更新时被用到。

　　很容易证明列间道路和它的更新区间是一一对应的关系。

　　所以修改某条列间道路时，只要顺着线段树往下找它对应的更新区间，做一次更新操作，再向上更新即可。

　　时间复杂度O(nlogn*更新常数)。（不知道出题人总时间开3s是什么心态……）

　　（合并操作写得像豆腐块一样）

#include <cstdio>
#include <cstring>
#include <algorithm>
#define MN 100005
#define l(a) (a<<1)
#define r(a) (a<<1|1)
using namespace std;
const int zx[2][2]={{0,2},{3,1}};
int lk[3][MN];
struct node
{
    int r; bool a[6]; //--/||
    friend node operator+(const node& a,const node& b)
    {
        node c;
        c.r=b.r;
        c.a[0]=a.a[0]&&lk[0][a.r]&&b.a[0]||a.a[2]&&lk[1][a.r]&&b.a[3];
        c.a[1]=a.a[1]&&lk[1][a.r]&&b.a[1]||a.a[3]&&lk[0][a.r]&&b.a[2];
        c.a[2]=a.a[0]&&lk[0][a.r]&&b.a[2]||a.a[2]&&lk[1][a.r]&&b.a[1];
        c.a[3]=a.a[1]&&lk[1][a.r]&&b.a[3]||a.a[3]&&lk[0][a.r]&&b.a[0];
        c.a[4]=a.a[4]||a.a[0]&&a.a[1]&&lk[0][a.r]&&lk[1][a.r]&&b.a[4];
        c.a[5]=b.a[5]||b.a[0]&&b.a[1]&&lk[0][a.r]&&lk[1][a.r]&&a.a[5];
        return c;
    }
}t[MN<<2];
int ct[MN][2];
int n;

inline int read()
{
    int n=0,f=1; char c=getchar();
    while (c<'0' || c>'9') {if(c=='-')f=-1; c=getchar();}
    while (c>='0' && c<='9') {n=n*10+c-'0'; c=getchar();}
    return n*f;
}

node getitv(int x,int L,int R,int ql,int qr)
{
    if (ql==L&&qr==R) return t[x];
    int mid=L+R>>1;
    if (qr<=mid) return getitv(l(x),L,mid,ql,qr);
    else if (ql>mid) return getitv(r(x),mid+1,R,ql,qr);
    else return getitv(l(x),L,mid,ql,mid)+getitv(r(x),mid+1,R,mid+1,qr);
}
void getcg2(int x,int L,int R,int ql,int qr)
{
    if (ql==L&&qr==R) {t[x]=t[l(x)]+t[r(x)]; return;}
    int mid=L+R>>1;
    if (qr<=mid) getcg2(l(x),L,mid,ql,qr);
    else if (ql>mid) getcg2(r(x),mid+1,R,ql,qr);
    t[x]=t[l(x)]+t[r(x)];
}
void getcg1(int x,int L,int R,int q)
{
    if (L==R) {t[x].a[2]^=1; t[x].a[3]^=1; t[x].a[4]^=1; t[x].a[5]^=1; return;}
    int mid=L+R>>1;
    if (q<=mid) getcg1(l(x),L,mid,q); else getcg1(r(x),mid+1,R,q);
    t[x]=t[l(x)]+t[r(x)];
}

void build(int x,int L,int R)
{
    if (L==R) {t[x].r=R; t[x].a[0]=t[x].a[1]=true; return;}
    int mid=L+R>>1;
    ct[mid][0]=L; ct[mid][1]=R;
    build(l(x),L,mid); build(r(x),mid+1,R);
    t[x]=t[l(x)]+t[r(x)];
}

int main()
{
    register int x1,y1,x2,y2,g;
    char c[10];
    n=read();
    build(1,1,n);
    for (scanf("%s",c);c[0]!='E';scanf("%s",c))
    {
        x1=read()-1; y1=read(); x2=read()-1; y2=read();
        if (c[0]=='O'||c[0]=='C')
        {
            if (x1==x2) {g=x1; if (y1>y2) swap(y1,y2);} else g=2;
            if (lk[g][y1]^(c[0]=='C')) continue;
            lk[g][y1]^=1;
            if (g==2) getcg1(1,1,n,y1); else getcg2(1,1,n,ct[y1][0],ct[y1][1]);
        }
        else if (c[0]=='A')
        {
            if (y1>y2) swap(x1,x2),swap(y1,y2);
            node lt=getitv(1,1,n,y1,y2),lt1,lt2;
            if (lt.a[zx[x1][x2]]) {puts("Y"); continue;}
            if (y1>1) lt1=getitv(1,1,n,1,y1-1);
            if (y2<n) lt2=getitv(1,1,n,y2+1,n);
            if (y1>1&&lt.a[zx[!x1][x2]]) if (lk[0][y1-1]&&lk[1][y1-1]&&lt1.a[5]) {puts("Y"); continue;}
            if (y2<n&&lt.a[zx[x1][!x2]]) if (lk[0][y2  ]&&lk[1][y2  ]&&lt2.a[4]) {puts("Y"); continue;}
            if (y1>1&&y2<n&&lt.a[zx[!x1][!x2]])
                if (lk[0][y1-1]&&lk[1][y1-1]&&lt1.a[5]&&lk[0][y2  ]&&lk[1][y2  ]&&lt2.a[4]) {puts("Y"); continue;}
            puts("N");
        }
    }
}

Last Word

　　小D当时就丢了一句“大力维护就好了啊”让小C茅塞顿开……

　　“初来乍到”、“毛遂自荐”、“喜出望外”、“病入膏肓”……出题人的语文水平还是值得肯定的。