找规律成功次数++。
Description
汉诺塔由三根柱子(分别用A B C表示)和n个大小互不相同的空心盘子组成。一开始n个盘子都摞在柱子A上,大的在下面,小的在上面,形成了一个塔状的锥形体。

对汉诺塔的一次合法的操作是指:从一根柱子的最上层拿一个盘子放到另一根柱子的最上层,同时要保证被移动的盘子一定放在比它更大的盘子上面(如果移动到空柱子上就不需要满足这个要求)。我们可以用两个字母来描述一次操作:第一个字母代表起始柱子,第二个字母代表目标柱子。例如,AB就是把柱子A最上面的那个盘子移到柱子B。汉诺塔的游戏目标是将所有的盘子从柱子A移动到柱子B或柱子C上面。有一种非常简洁而经典的策略可以帮助我们完成这个游戏。首先,在任何操作执行之前,我们以任意的次序为六种操作(AB、AC、BA、BC、CA和CB)赋予不同的优先级,然后,我们总是选择符合以下两个条件的操作来移动盘子,直到所有的盘子都从柱子A移动到另一根柱子:(1)这种操作是所有合法操作中优先级最高的;(2)这种操作所要移动的盘子不是上一次操作所移动的那个盘子。可以证明,上述策略一定能完成汉诺塔游戏。现在你的任务就是假设给定了每种操作的优先级,计算按照上述策略操作汉诺塔移动所需要的步骤数。
Input
输入有两行。第一行为一个整数n,代表盘子的个数。第二行是一串大写的ABC字符,代表六种操作的优先级,靠前的操作具有较高的优先级。每种操作都由一个空格隔开。
Output
只需输出一个数,这个数表示移动的次数。
Sample Input
3
AB BC CA BA CB AC
Sample Output
7
HINT
1≤n≤30,保证答案不会超过10^18。
Solution
先来说说DP(实际上是递推)的做法。
由于操作序列的优先级是固定的,那么对于每种操作序列,它的移动自始至终都是唯一的。所以我们称之为递推。
Hanoi问题还有一个经典性质就是,它的整个过程是可以用递归实现的。
用f[i][j]表示前i小的盘子现在全部堆叠在第j座塔上,把这i个盘子全部移到另一座塔上需要的步数。
不管这i个盘子下面还有没有盘子,f[i][j]是固定的(显然很好证明)。这就可以看出这个问题有很好的子任务性。
所以我们依然以上面提到的f[i][j]设计状态,顺便记录g[i][j]为这i个盘子从第j座塔移到了哪一座塔。
接着就可以愉快地考虑转移了:
首先操作序列是固定的,f[1][j]和g[1][j]都可以确定。
当i>1时,我们分类讨论一下。
先把i-1个盘子从j用f[i-1][j]的步数移到g[i-1][j],然后第i个盘子就只能够移到剩下的那座塔,设这座塔为k。
然后要做的事是把位于g[i-1][j]的i-1个盘子移到k上。
如果g[i-1][g[i-1][j]]=k,那么万事大吉,直接花费f[i-1][g[i-1][j]]的步数完成转移;
如果g[i-1][g[i-1][j]]≠k,那么它只能等于j,无奈之下先把这i-1个盘子先移到j,
然后第i个盘子又只能够从k移到g[i-1][j],由于g[i-1][j]=g[i-1][j],这下可以放心地把这i-1个盘子放到第i个盘子上了。
总的转移方程为:
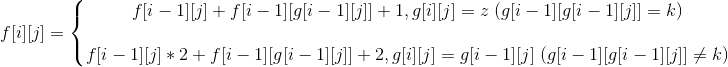 。
。
然而小C刚开始做这题的的时候是没啥头绪的,所以开始打表找规律。
打表之前,有一个显而易见的结论:
每次移动的起点总是确定的,而终点可能确定也可能不确定。
就拿n=3,“AB BC CB AC BA CA”为例:
第一步,起点只能为“A”,终点可以是“B”、“C”,因为“AB”在“AC”前面,所以从把盘子从“A”挪到“B”→{2,3}{1}{};
第二步,起点只能为“A”,终点只能为“C”→{3}{1}{2};
第三步,起点只能为“B”,终点可以是“A”、“C”,“BC”在“BA”前面→{3}{}{1,2};
第四步,起点只能为“A”,终点只能为“B”→{}{3}{1,2};
第五步,起点只能为“C”,终点只能为“A”、“B”,“CB”在“CA”前面→{}{1,3}{2}……
注意第五步本来的最优走法是“CA”,而走“CB”导致最终步数为9而不是7。
所以能够影响答案的只有“AB”与“AC”之间,“BA”与“BC”之间,“CA”与“CB”之间的相对位置关系。
又由于“B”和“C”本质上是相同的,“AB”和“AC”本质上也是相同的,所以当n确定时,答案不会超过4种。
实际上,小C打表出来的答案只有3种。而且这3种的步数还分别是关于n的一阶递推式!
结论如下:f[1]=1,假设“AX”在“AY”前面。
若“XA”在“XY”前面,递推式为f[x]=f[x-1]*3+2;
若“XY”在“XA”前面且“YX”在“YA”前面,递推式为f[x]=f[x-1]*3;
若“XY”在“XA”前面且“YA”在“YX”前面,递推式为f[x]=f[x-1]*2+1。
小C也只能推导到这了,至于为什么是递推式,网络上其他题解也有证明。
但至于为什么是这几个递推式,就有待研究了,小C也不会证明,读者如有想法可以发表评论或是联系小C。
DP法:
#include <cstdio> #include <cstring> #include <algorithm> #define MN 35 #define ll long long using namespace std; char c[3]; ll f[MN][3]; int g[MN][3]; int n; inline int read() { int n=0,f=1; char c=getchar(); while (c<'0' || c>'9') {if(c=='-')f=-1; c=getchar();} while (c>='0' && c<='9') {n=n*10+c-'0'; c=getchar();} return n*f; } int main() { register int i,x,y,z; n=read(); for (i=1;i<=6;++i) { scanf("%s",c); if (!g[1][c[0]-'A'+1]) g[1][c[0]-'A'+1]=c[1]-'A'+1; } f[1][1]=f[1][2]=f[1][3]=1; for (i=2;i<=n;++i) for (x=1;x<=3;++x) { y=g[i-1][x]; z=6-x-y; if (g[i-1][y]==z) f[i][x]=f[i-1][x]+f[i-1][y]+1,g[i][x]=z; else f[i][x]=f[i-1][x]*2+f[i-1][y]+2,g[i][x]=y; } printf("%lld",f[n][1]); }
观察找规律法:
#include <cstdio> #include <cstring> #include <algorithm> #define ll long long using namespace std; ll ans; int n,mov[3]; char a[6][6]; inline int read() { int n=0,f=1; char c=getchar(); while (c<'0' || c>'9') {if(c=='-')f=-1; c=getchar();} while (c>='0' && c<='9') {n=n*10+c-'0'; c=getchar();} return n*f; } int main() { register int i; n=read(); for (i=0;i<6;++i) scanf("%s",a[i]); for (i=5;i>=0;--i) mov[a[i][0]-'A']=a[i][1]-'A'; ans=1; if (mov[mov[0]]==0) {for (i=2;i<=n;++i) ans=ans*3+2;} else if (mov[mov[mov[0]]]==mov[0]) {for (i=2;i<=n;++i) ans=ans*3;} else {for (i=2;i<=n;++i) ans=ans*2+1;} printf("%lld",ans); }
Last Word
有一次通过自己瞎搞找出规律的经历还是很赛艇的。
题目中操作的720种排列方式明摆着就在告诉你,来打表找规律吧~
不过递推的方法也算让小C知道了Hanoi的一个经典性质。