Dima and Lisa

Dima and Lisa

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Dima loves representing an odd number as the sum of multiple primes, and Lisa loves it when there are at most three primes. Help them to represent the given number as the sum of at most than three primes.

More formally, you are given an odd numer n. Find a set of numbers pi (1 ≤ i ≤ k), such that

1. 1 ≤ k ≤ 3
2. pi is a prime
3. 

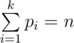
The numbers pi do not necessarily have to be distinct. It is guaranteed that at least one possible solution exists.

Input

The single line contains an odd number n (3 ≤ n < 109).

Output

In the first line print k (1 ≤ k ≤ 3), showing how many numbers are in the representation you found.

In the second line print numbers pi in any order. If there are multiple possible solutions, you can print any of them.

Sample test(s)

input

27

output

3
5 11 11

Note

A prime is an integer strictly larger than one that is divisible only by one and by itself.

 哥德巴赫猜想：

　　　　两个素数差距不超过800；

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
bool is_prime(int n){
    for(int i = 2; i <= sqrt(n); i++){
        if(n%i == 0)return 0;
    }
    return 1;
}
int main(){
    int n;
    scanf("%d",&n);
    if(is_prime(n))
        printf("1
%d",n);
    else if(is_prime(n-2))
        printf("2
%d 2",n-2);
    else if(is_prime(n-4))
        printf("3
%d 2 2",n-4);
    else {
        for(int i = 3;; i++){
            int m = n - i;
            for(int j = 3; j < m; j += 2){
                if(is_prime(m-j) && is_prime(j)){
                    printf("3
%d %d %d",m-j,j,i);
                    return 0;
                }
            }
        }
    }
    return 0;
}