Codeforce922C (Cave Painting)

C. Cave Painting

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Imp is watching a documentary about cave painting.

Some numbers, carved in chaotic order, immediately attracted his attention. Imp rapidly proposed a guess that they are the remainders of division of a number n by all integers i from 1 to k. Unfortunately, there are too many integers to analyze for Imp.

Imp wants you to check whether all these remainders are distinct. Formally, he wants to check, if all 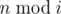, 1 ≤ i ≤ k, are distinct, i. e. there is no such pair (i, j) that:

• 1 ≤ i < j ≤ k,
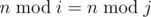• , where 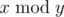is the remainder of division x by y.

Input

The only line contains two integers n, k (1 ≤ n, k ≤ 10¹⁸).

Output

Print "Yes", if all the remainders are distinct, and "No" otherwise.

You can print each letter in arbitrary case (lower or upper).

Examples

Input

Copy

4 4

Output

No

Input

Copy

5 3

Output

Yes

Note

In the first sample remainders modulo 1 and 4 coincide.

　　分析：假设N mod 1~k的每个余数都不同，那么因为N mod 1=0,

　　　　所以N mod 2=1...... N mod k=k-1，能满足这些的k不会很大，想象一下k的阶乘，

　　　　暴力出奇迹=_=

　　

#include<cstdio>
int main()
{
    long long N,k;
    scanf("%lld%lld",&N,&k);
    int flag=0;
    for(long long i=1;i<=k;i++)
    if(N%i!=(i-1)) {flag=1;break;}
    if(flag) printf("No
");
    else printf("Yes
");
    return 0;
}