数据结构中经常考察的一个点就是并查集。
并查集(Union-find Sets)是一种非常精巧而实用的数据结构,它主要用于处理一些不相交集合的合并问题。
百度百科上的定义是这样的:并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中,其特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往在空间上过大,计算机无法承受;即使在空间上勉强通过,运行的时间复杂度也极高,根本就不可能在比赛规定的运行时间(1~3秒)内计算出试题需要的结果,只能用并查集来描述。
但是百科上的语言文字往往容易让人失去了兴趣,所以接下来我将以比较通俗易懂的语言来描述一下并查集,希望大家能够有所收获
现在我们来看一道十分明显的并查集问题:
【问题描述】
一家公司有n名员工,刚开始每个人单独构成一个工作团队。
有时一项工作仅凭一个人或一个团队难以完成,所以公司会让某两个人所在的团队合并。
但有的工作属于闷声大发财类型的,不适合多人做,所以公司有时也会让一个人从他当前所在的团队中分离出来,构成单独的团队。
公司也要对当前团队的情况进行了解,所以他们也会询问一些问题,比如某两个人是否属于同一工作团队,某个人所在的团队有多少个人,或者当前一共有多少个工作团队。
作为该公司的软件服务商,你的任务便是实现一个实时的操作和查询系统。
【输入格式】
每个测试点第一行有两个正整数n,m,表示员工数和公司的指令数。
接下来m行,每行的格式为下列所述之一:
1 u v,表示将第u个人与第v个人所在的团队合并,如果两个人所在团队相同,则不执行任何操作。
2 w,表示使第w个人从当前的团队中分离出来,如果第w个人不在任何多人团队中,则不执行任何操作。
3 x y,表示询问x,y两个人是否在同一个工作团队,是的话回答Yes,否则回答No。
4 z,表示询问第z个人所在的工作团队一共有多少个人。
5,询问当前一共有多少个工作团队。
【输出格式】
对每个询问输出一行相应的值表示答案。
【样例输入】
3 11
1 1 2
3 2 3
4 2
1 2 3
3 2 3
4 2
5
2 2
3 2 3
4 2
5
【样例输出】
No
2
Yes
3
1
No
1
2
【数据规模】
Easy:对于30%的数据,不存在2,4,5操作。
Normal:对于70%的数据,不存在2操作。
Hard:对于100%的数据,均有1 ≤ n ≤ 50000,1 ≤ m ≤ 100000
对于我们这种刚刚接触并查集的新手来说显然是有些艰难的,所以我们现在就必须要了解一下并查集是如何工作的。
并查集首先就是先把自己指向自己做自己的父亲,等到后面找别人来做自己的父亲,一层一层递归上去,然后两个父亲互相认识一下就行了。
我们用通俗易懂的江湖语言来描述一遍吧!
【通俗易懂】:
在金庸小说的世界里,门派很多,经常会发生一些争斗,而且一般来说一个大的势力首先都需要自己出头来做老大,所以这个时候你自己的这个门派的老大就是你自己,即father[you]=you
后来,在你冒险的过程中你开始结识了一群很牛逼的好友,你觉得应该把他们拉到自己的门下,那么这个时候你就劝说他们把他们的门派老大指向你,意思就是说你是他们的老大,即father[别人]=you
但是你只是认识了这些比你低一级别的属下,你属下的属下和他属下的属下都互相不认识啊,这个时候就很容易起争端还不知道是自己人,互相打来打去(怎么这么傻),万一有一天在小树林里碰面,A、B二人都不知道对方是敌是友,如果要一级一级上报上去,显然是可以做到的,但是其中所耗费的时间必然是我们所比较不愿意接受的,所以我们希望我们属下的属下,他的老板就是我,意思就是说他可以直接认识我,并且接触到我,这样的话两人看到,就可能说:“在下是不甜薄荷叶的属下”,“诶,我是不甜薄荷叶他属下很甜薄荷叶的属下,我们两个是朋友”然后两个人就手拉手一起走上人生巅峰了。。。。。这里的代码转换一下即:判断一下是敌是友(int x=find(A),y=find(B)解释:x是A的顶头上司,y是B的顶头上司)如果不认识,那么认识一个朋友就是一个保障嘛,那么这个时候:father[x]=y,但是你会发现如果这样,一层一层地上报岂不是很麻烦,那么你就可以直接father[A]=y就可以啦,这就是一个非常简单的路径压缩啦
这样其实我们就把并查集的工作原理讲完了,现在我们用一些短小的代码来实现一下并查集。
CODE1://初始化每一个节点,一开始我们应该让所有节点都自己做老大,自己指向自己
1 void initialise(){ 2 for(int i=1;i<=n;i++) 3 father[i]=i; 4 }
CODE2://找父节点的操作,一般都是可以直接用递归就可以找到,也可以用while循环来实现
1 int find(int x){ 2 if(x!=father[x])father[x]=find(father[x]); 3 return father[x]; 4 }
CODE3://合并两个节点的操作,直接把自己的父节点指向对方就可以了,但是这样会存在一定的缺点,我们下面再继续陈述
1 void unionn(int x,int y){ 2 x=find_fa(x); 3 y=find_fa(y); 4 father[y]=x; 5 return; 6 }
在这样的情况下我们的并查集其实就可以解决啦。
然后我们再回到我们最初的那一道题目,基本就是裸的并查集啦。
但是这里面的难点就是在于把一个点分离出来。
那么怎么做呢?其实我们可以考虑把这个点假装还在原来的集合内,但是实际上它已经不在了,我们只需要一个stand标志数组,表示我当前的这个节点实际上到底在哪个节点内就可以啦
在树结构的并查集中,我们要使一个点从树中分离出来是一件很麻烦的事。为了保持树结构的完整,对于每次分离操作,我们为相应的点u新建立一个节点,表示独立出来的u,而原来的节点表示旧的u节点,它起到连接节点与保持树结构的作用,在此之后对节点u的操作均在新建立的节点上进行即可。注意分离的时候要维护好原来的集合的size值和集合数。
这样我们这一题也就结束啦!!!
CODE4:
1 #include<bits/stdc++.h> 2 using namespace std; 3 int father[1000002],size[1000002],n,m,u,v,w,peo1,peo2,peo3,ans=0,tot,stand[1000002]; 4 int find(int x){ 5 if(x!=father[x])father[x]=find(father[x]); 6 return father[x]; 7 } 8 void unionn(int x,int y){ 9 int r1=find(stand[x]); 10 int r2=find(stand[y]); 11 if(r1==r2)return; 12 else { 13 size[r1]+=size[r2]; 14 size[r2]=0; 15 father[r2]=r1; 16 ans--; 17 } 18 return; 19 } 20 void break_up(int x){ 21 int fin=find(stand[x]); 22 if(size[fin]<=1)return; 23 else { 24 tot++; 25 stand[x]=tot; 26 father[tot]=stand[x]; 27 size[fin]--;size[tot]=1; 28 ans++; 29 } 30 return; 31 } 32 void work(){ 33 scanf("%d%d",&n,&m); 34 tot=ans=n; 35 for(int i=1;i<=n;i++){ 36 father[i]=i; 37 size[i]=1; 38 stand[i]=i; 39 } 40 int temp; 41 for(int i=1;i<=m;i++){ 42 scanf("%d",&temp); 43 switch (temp){ 44 case 1:{ 45 scanf("%d%d",&u,&v); 46 unionn(u,v); 47 break; 48 } 49 case 2:{ 50 scanf("%d",&w); 51 break_up(w); 52 break; 53 } 54 case 3:{ 55 scanf("%d%d",&peo1,&peo2); 56 if(find(stand[peo1])==find(stand[peo2]))printf("Yes "); 57 else printf("No "); 58 break; 59 } 60 case 4:{ 61 int num; 62 scanf("%d",&peo3); 63 num=find(stand[peo3]); 64 printf("%d ",size[num]); 65 break; 66 } 67 default:{ 68 printf("%d ",ans); 69 break; 70 } 71 } 72 } 73 return; 74 } 75 int main(){ 76 work(); 77 return 0; 78 }
现在我们再回到我刚刚留下的那个坑(为什么会有缺点呢)?
我们来看一下下面的图片:假设一直父节点相互连接的结果就是这样的,就会导致说查询的长度会过长,时间的代价会很高(用江湖话来说就是我问一件事情都要一层一层上报,等到花儿都谢了!!!:
那如果要S和T连起来,那么显然是右边的那一图是更优的方式,查找的速率是几乎为O(1)的,在合并的过程中就已经把路径给压缩了一下


右边的那种操作实际上就是路径压缩(这里不再详细介绍)
我们以一张参考图片作为结尾: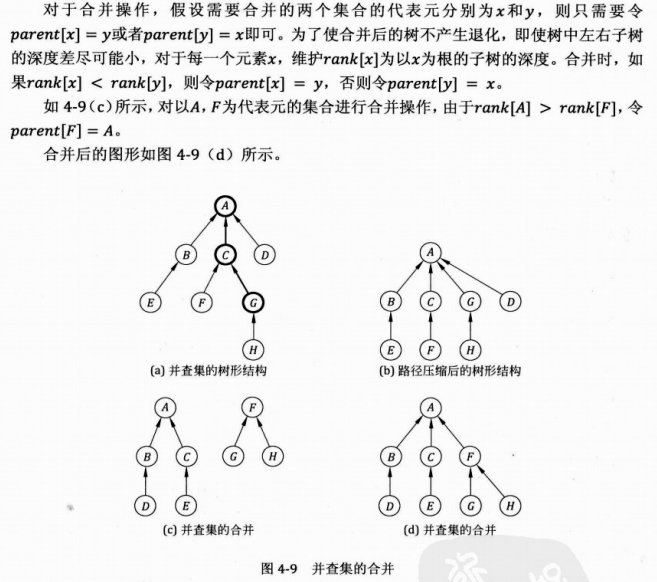
希望这篇看起来非常水的博客对您有所帮助!!!