题目大意
给定一棵二叉树,每个结点 \(u\) 上有一个小写字母 \(c_u\)。对这棵二叉树进行中序遍历,将结点上的字母按中序遍历的顺序相连成一个字符串。你可以选择至多 \(k\) 个结点,对于每个被选的结点 \(u\),将其上的字符串由 \(c_u\) 改为 \(c_uc_u\)(即复制一遍 \(c_u\) 这个字符)。要求如果结点 \(u\) 被选中,则它的父亲也一定要被选中。求选择至多 \(k\) 个结点后,中序遍历得到的字典序最小的字符串是多少。
题解
首先我们可以求出未修改的树通过中序遍历得到的字符串为 \(s\)。然后可以求出哪些结点被选中可以导致 \(s\) 的字典序变小(若在 \(s\) 中,\(s_i\) 右边第一个不等于 \(s_i\) 的字符 \(s_j>s_i\),则选中 \(s_i\) 所代表的结点可以导致 \(s\) 的字典序变小),我们称这些点为好点,最好情况肯定是好点全被选,其它点全不被选,这样字典序最小。但因为最多只能选 \(k\) 个点,所以我们优先选 \(s\) 中靠左的好点。又因为选中一个点同时也要选中该点的父亲,而该点的父亲可能不是好点,于是我们不希望出现该点的父亲不是好点,但该点的父亲在中序遍历中在该点的前面这一情况(即好点是父亲的右儿子,父亲不是好点),除非父亲的左子树中选了一个好点。
于是可以发现我们最终所选择的所有点实际上是若干条左偏链:
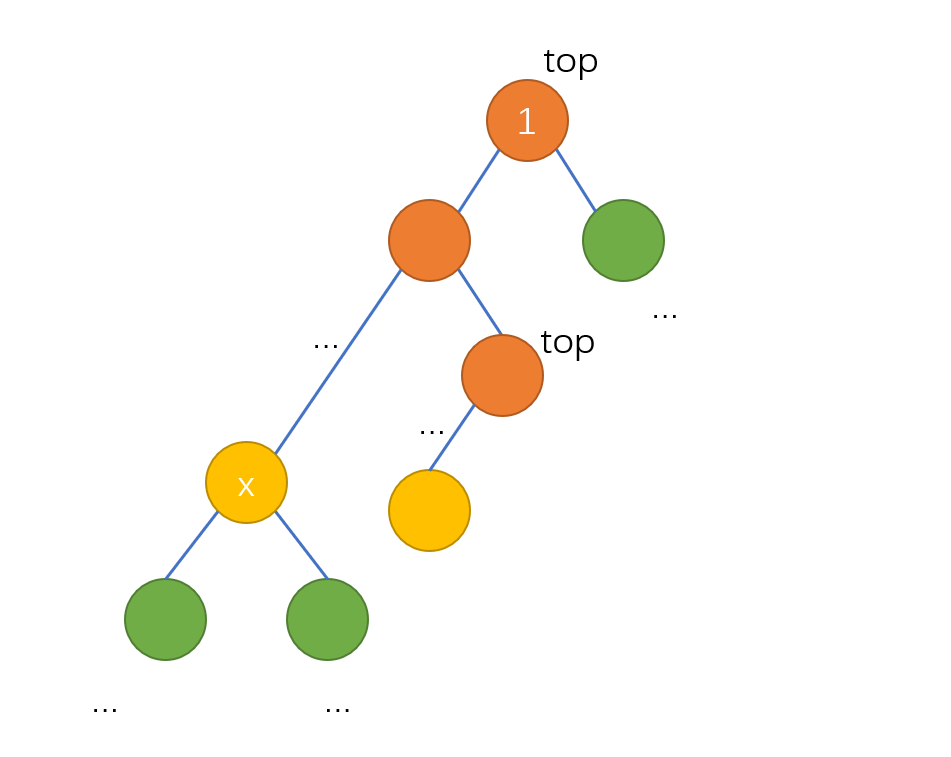
然后就是在最多选 \(k\) 个点的情况下尽可能长且尽可能多地选择左偏链,具体实现可以参考树链剖分中划分树链的方式,即DFS时下传每条链的链顶。
最终的时间复杂度为 \(O(n)\)。
Code
#include <bits/stdc++.h>
using namespace std;
int T[200010][2], tid[200010], deep[200010];
char s[200010], t[200010];
bool mark[200010], mark2[200010];
int n, k, idx;
void DFS(int u) {
if (T[u][0]) { deep[T[u][0]] = deep[u] + 1; DFS(T[u][0]); }
tid[++idx] = u;
t[idx] = s[u];
if (T[u][1]) { deep[T[u][1]] = deep[u] + 1; DFS(T[u][1]); }
}
bool DFS2(int u, int top) {
bool flag = false;
if (T[u][0]) { if (DFS2(T[u][0], top)) flag = true; }
if (flag) mark2[u] = true;
if (mark[u] && !flag) {
if (deep[u] - deep[top] + 1 <= k) {
k -= (deep[u] - deep[top] + 1);
mark2[u] = true;
flag = true;
}
}
if (T[u][1] && flag) DFS2(T[u][1], T[u][1]);
return flag;
}
int main() {
scanf("%d%d", &n, &k);
scanf("%s", s + 1);
for (int i = 1;i <= n;++i)
scanf("%d%d", &T[i][0], &T[i][1]);
DFS(1);
int p = n;
for (int i = n;i >= 1;--i) {
if (t[p] > t[i]) mark[tid[i]] = true;
if (t[i - 1] != t[i]) p = i;
}
DFS2(1, 1);
for (int i = 1;i <= n;++i) {
printf("%c", t[i]);
if (mark2[tid[i]]) printf("%c", t[i]);
}
printf("\n");
return 0;
}