前言
树形 DP 是 NOIP/CSP 常考类型,是最重要的 DP。
由于树固有的递归性质,树形 DP 一般都是递归进行的。
- Upd \(1\):增加点分治相关内容。
基础
以下面 【LG P1352】没有上司的舞会 为例,介绍一下树形 DP 的一般过程。
题目大意:某大学有 \(n\) 个职员,编号为 \(1\sim n\)。他们之间有从属关系,父结点就是子结点的直接上司。现在有个周年庆宴会,宴会每邀请来一个职员都会增加一定的快乐指数 \(a_i\),但是,如果某个职员的上司来参加舞会了,那么这个职员就不肯来参加舞会了。求最大的快乐指数。
我们可以定义 \(f_{i,0/1}\) 代表以 \(i\) 为根的子树的最优解(第二维的值为 \(0\) 代表 \(i\) 不参加舞会的情况,\(1\) 代表 \(i\) 参加舞会的情况)。
显然,我们可以推出下面两个状态转移方程(其中下面的 \(v\) 都是 \(u\) 的儿子,下同):
-
\(f_{u,0}=\sum_{\text{edge}(u,v)}\max\{f_{v,1},f_{u,0}\}\)(上司不参加舞会时,下属可以参加,也可以不参加)
-
\(f_{u,1}=\sum_{\text{edge}(u,v)}f_{u,0}+a_i\)(上司不参加舞会时,下属可以参加,也可以不参加)
我们可以通过 dfs,在返回上一层时更新当前结点的最优解。
代码:
#include<bits/stdc++.h>
using namespace std;
int a[6005],f[6005][2];
vector<int> v[6005];
bool staff[6005];
void dp(int x) {
f[x][0]=0;
f[x][1]=a[x];
for(int i=0; i<v[x].size(); i++) {
int t=v[x][i];
dp(t);
f[x][0]+=max(f[t][0],f[t][1]);
f[x][1]+=f[t][0];
}
}
int main() {
int n;
scanf("%d",&n);
for(int i=1; i<=n; i++) {
scanf("%d",a+i);
}
for(int i=1; i<=n; i++) {
int x,y;
scanf("%d %d",&x,&y);
v[y].push_back(x);
staff[x]=1;
}
int root;
for(int i=1; i<=n; i++) {
if(!staff[i]) {
root=i;
}
}
dp(root);
printf("%d",max(f[root][0],f[root][1]));
return 0;
}
相关练习:【LG P2016】战略游戏。
树上背包
树形背包解决的问题是给你几个物品,但物品有依赖关系,\(a\) 依赖 \(b\),\(b\) 依赖 \(c\),选 \(a\) 就必须选 \(b\),选 \(b\) 就必须选 \(c\),一个物品只能依赖一个物品,但一个物品可以被多个物品依赖,这里就能看出来这是一个树。叫你选择 \(n\) 物品可以使得价值最大,价值为多少。
一般我们的状态就是 \(f_{i,j}\) 表示以 \(i\) 为根节点的子树中选择了 \(j\) 个点所得到的价值,转移也大都是利用 dfs 回溯和背包来进行。
以下面 【CTSC 1997】选课 为例,介绍一下树形背包。
题目大意:有一堆树构成的森林,共 \(n\) 个点。每个点有一个权值 \(s_i\)。一个点可以被选择,当且仅当它到根节点的路径上的所有点都被选择。共选择 \(m\) 个点,求被选择的点的权值和的最大值。
一个小技巧:我们发现,如果 \(0\) 算一个节点的话,整张图就是一棵树了。
这样的好处:
一棵树就不用分别考虑各棵树然后合并了。输入方便很多,不用特别处理 \(0\) 的情况。但是 \(m\) 就会受影响。
因为根节点 \(0\) 是必选的,所以只要让 \(m\) 增加 \(1\) 就好了。
首先,不难看出,父节点的信息可以由子节点合并得到并且不会影响子节点。
所以使用 dp 或者记忆化搜索就好了。
不难想到,用 \(dp_{u,i}\) 表示以节点 \(u\) 为根的子树,选择 \(i\) 个点可以获得的最大权值和。然后想如何转移。
好像遇到麻烦了!
显然合并子节点的信息一定能得到父节点的信息,但使用简单的算法好像不行了。
没事反正数据范围小。
继续观察,发现每个子节点都会占用父节点 \(i\) 的一部分,又有一个贡献,可以选择或不选择。
重量……价值……总重……这不是 \(01\) 背包吗?
不同之处在于,每个子节点的重量都是变量。
重新设计状态,用 \(dp_{u,i,j}\) 表示节点 \(u\) 的前 \(i\) 个子节点,限重为 \(j\) 能得到的最大权值和(价值和)
像 \(01\) 背包一样压缩空间,得到:
\(dp_{i,j}\) 表示节点 \(u\),限重 \(j\) 的最大权值和(价值和)。
for(int i=head[u]; i; i=e[i].nxt) {
int v=e[i].to;
dp(v);
for(int j=m+1; j; j--) {
for(int k=0; k<j; k++) {
f[u][j]=max(f[u][j],f[v][k]+f[u][j-k]);
}
}
}
相关练习:
-
【LG P1273】有线电视网 树上分组背包经典题。
转移方程 \(dp_{i,j}=\max(dp_{i,j},dp_{i,j-k}+dp_{v,k}-w)\)。\(v\) 表示枚举到这一组(即 \(i\) 的儿子),\(w\) 指这条边的边权,\(k\) 表示枚举到这组中的元素:选 \(k\) 个用户。
-
【LG P1272】重建道路 类似树上背包的树形 DP。
递归操作,\(f_{i,j}\) 表示保留 \(i\) 为根的子节点。\(c\) 数组记录点的度。因为这是一棵树,所以每个点的度为 \(1\)。然后随便设一个根,我设的 \(1\) 为根,\(1\) 的根就为 \(0\)。递归时传入两个参数,为当前节点和当前节点的根。
换根 DP
树形 DP 中的换根 DP 问题又被称为二次扫描,通常不会指定根结点,并且根结点的变化会对一些值,例如子结点深度和、点权和等产生影响。
通常需要两次 dfs,第一次 dfs 预处理诸如深度,点权和之类的信息,在第二次 dfs 开始运行换根动态规划。
接下来以例题 【POI 2008】STA-Station 来带大家熟悉这个内容。
题目大意:给定一个 \(n\) 个点的树,请求出一个结点,使得以这个结点为根时,所有结点的深度之和最大。
如果我们假设某个节点为根,将无根树化为有根树,在搜索回溯时统计子树的深度和,则可以用一次搜索算出以该节点为根时的深度和,其时间复杂度为 \(O(n)\)。
但这样求解出的答案只是以该节点为根的,并不是最优解。如果要暴力求解出最优解,则要枚举所有的节点为根,然后分别跑一次搜索,这样的时间复杂度会达到 \(O(n^2)\),显然不可接受。
因此考虑在第二次搜索时就完成所有节点答案的统计。
假设第一次搜索时的根节点为 \(1\) 号节点,则此时只有 \(1\) 号节点的答案是已知的。同时第一次搜索可以统计出所有子树的大小。
第二次搜索依旧从 \(1\) 号节点出发,若1号节点与节点x相连,则我们考虑能否通过1号节点的答案去推出节点x的答案。
假设此时将根节点换成节点 \(x\),则其子树由两部分构成,第一部分是其原子树,第二部分则是 \(1\) 号节点的其他子树(如下图)。
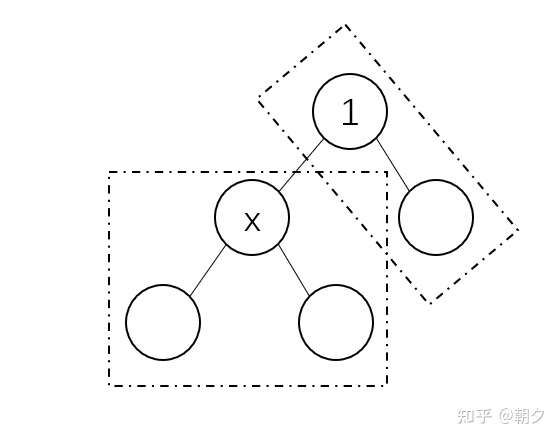
根从 \(1\) 号节点变为节点 \(x\) 的过程中,我们可以发现第一部分的深度降低了 \(1\),第二部分的深度则上升了 \(1\),而这两部分节点的数量在第一次搜索时就得到了。
代码:
#include<bits/stdc++.h>
using namespace std;
using LL=long long;
const int N=1e6+5;
struct edge {
int to,nxt;
} e[N<<1];
int n,cnt,id;
int head[N];
LL ans,f[N],dep[N],siz[N];
inline void add(int u,int v) {
e[++cnt].nxt=head[u],head[u]=cnt,e[cnt].to=v;
}
void dfs1(int u,int fa) {
siz[u]=1,dep[u]=dep[fa]+1;
for(int i=head[u]; i; i=e[i].nxt) {
int v=e[i].to;
if(v==fa) {
continue;
}
dfs1(v,u),siz[u]+=siz[v];
}
}
void dfs2(int u,int fa) {
for(int i=head[u]; i; i=e[i].nxt) {
int v=e[i].to;
if(v==fa) {
continue;
}
f[v]=f[u]+n-2*siz[v],dfs2(v,u);
}
}
int main() {
scanf("%d",&n);
for(int i=1,u,v; i<n; i++) {
scanf("%d %d",&u,&v),add(u,v),add(v,u);
}
dfs1(1,0);
for(int i=1; i<=n; i++) {
f[1]+=dep[i];
}
dfs2(1,0);
for(int i=1; i<=n; i++) {
if(ans<f[i]) {
ans=f[i],id=i;
}
}
printf("%d",id);
return 0;
}
相关练习:
- 【USACO10MAR】Great Cow Gathering G 一道经典的换根 dp 问题。考虑 \(f_i\) 表达以 \(i\) 为根子树中奶牛到 \(i\) 的距离和。第一次 dfs 从下至上递推出各点的 \(f_i\) 和子树奶牛数 \(siz_i\)。画图易知每个点的答案 \(f_i\) 满足的方程 \(f_v=f_u-siz_v\times w+(sum-siz_v)\times w\)。
- 【CF 708C】Centroids 一道换根 DP 好题。相关思路请看 题解。
基环树
基环树就是有 \(n\) 个点 \(n\) 条边的图,由于比树只出现了一个环,那么就称之为基环树了。
基环树结构仍然很简单,但比树要恶心。
接下来将特殊形态的基环树:
-
无向树(无向图):
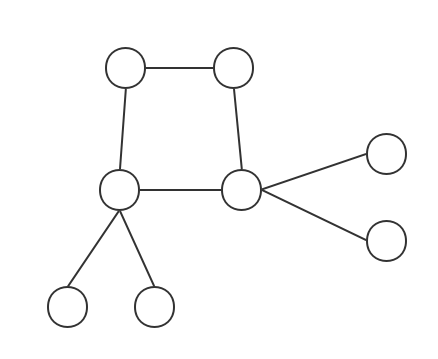
-
外向树(每个点只有一条入边):
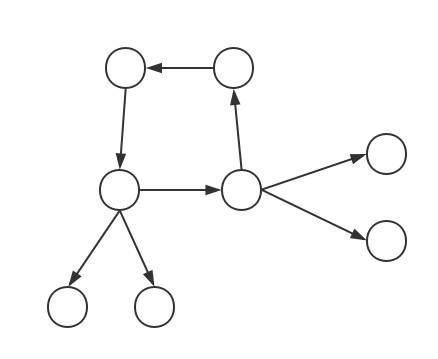
-
内向树(每个点只有一条出边):
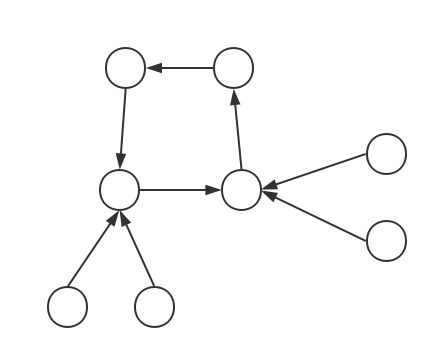
以上三种树有十分优秀的性质,就是可以直接将环作为根。就可以对每个环的子树进行单独处理,最后再处理环。
找环有两种方法:
1. 拓扑排序
处理无向图,可以找出环上的所有点。
void topsort() {
queue<int> q;
for(int i=1; i<=n; i++) {
if(in[i]==1) {
q.push(i);
}
}
while(q.size()) {
int u=q.front();
q.pop();
for(int i=head[u]; i; i=e[i].nxt) {
int v=a[i].to;
if(in[v]>1) {
in[v]--;
if(in[v]==1) {
q.push(v);
}
}
}
}
}
之后入度 \(\ge2\) 的点就是环上的点。
2. dfs
处理有向图,码量小。
void check_c(int x)
{
v[x]=true;
if(v[d[x]]) mark=x;
else check_c(father[x]);
return;
}
mark 就是环上的一个点。
接下来以例题 【LG P1453】城市环路 来带大家熟悉这个内容。
题目大意:给你一棵树,点有点权,强制要求一条边只能选一个点,并且还额外命令 \((S,T)\) 也不能同时选,求满足条件下的最大贡献。
这不是摆明了那你用树形 DP 切掉的节奏吗?
设 \(f_{u,0/1}\) 表示以 \(u\) 为根的字树,\(u\) 点选或不选的最大贡献。
然后转移比较显然:
- 如果 \(u\) 点要选,则它所有的儿子都不能选。
- 如果 \(u\) 点不选,那么它的儿子可以选也可以不选。
所以转移式就是:
然后考虑最后的统计答案。
以 \(S,T\) 两点分别做一次 dp,然后在 \(f_{s,0},f_{t,0}\) 中取较大值,这样就能保证 \(S,T\) 不可能同时被选了。
相关练习:
- 【IOI 2008】Island 基环树直径问题。
点分治
前言
点分治,是一种处理树上路径问题的工具,举个例子:
给定一棵树和一个整数 \(k\),求树上边数等于 \(k\) 的路径有多少条。
做法很简单,枚举不同的两个点,然后 dfs 算出它们间的距离,统计一下就行了。大概是 \(O(n^3)\) 的复杂度。
布星啊 \(n\) 大一点就搞不了。
那找个根,求出每个点到根的距离,然后枚举两个点,求 lca,简单加减一下就行了。
大概是 \(O(n^2\log n)\) 的复杂度?
还是布星啊 \(n\) 还要大,几万的数据就搞不了了怎么这么多事……
考虑一下形成路径的情况,假设一条满足条件的路径经过点 \(x\),那么这条路径在 \(x\) 的一个子树里(以 \(x\) 为端点)或者在 \(x\) 的两个不同的子树里,如图:
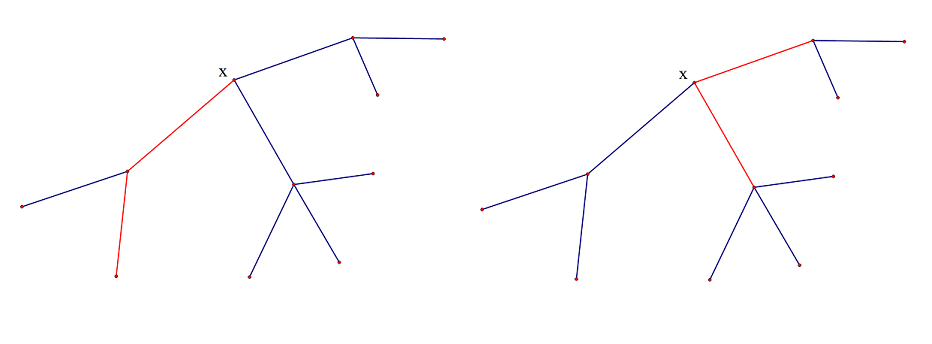
一个好的想法是找到一个根,然后 \(dfs\) 遍历子树中的每个点,依次处理每个点的子树答案。
原理
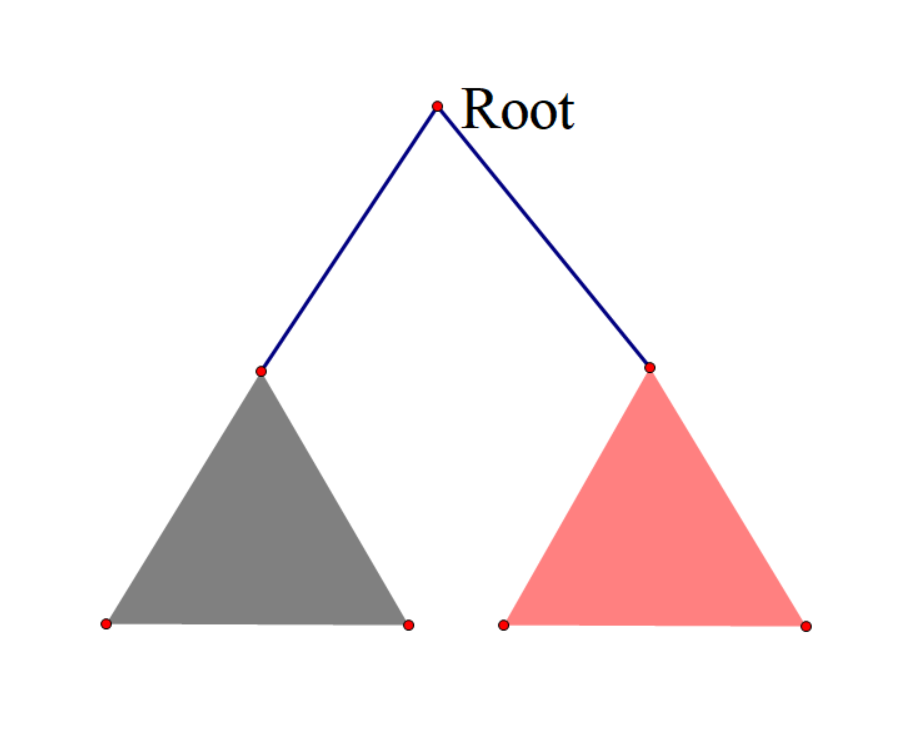
如图,假设我们选出一个根 Root,那么答案路径肯定是要么被一个子树所包含,要么就是跨过 Root,在黑子树中选择一部分路径,在红子树中选择一部分路径,然后从 Root 处拼起来形成一条答案路径。
仔细想一下,发现情况 \(1\)(被一个子树包含)中,答案路径上的一点变为根 Root,就成了情况 \(2\)(在两棵子树中)
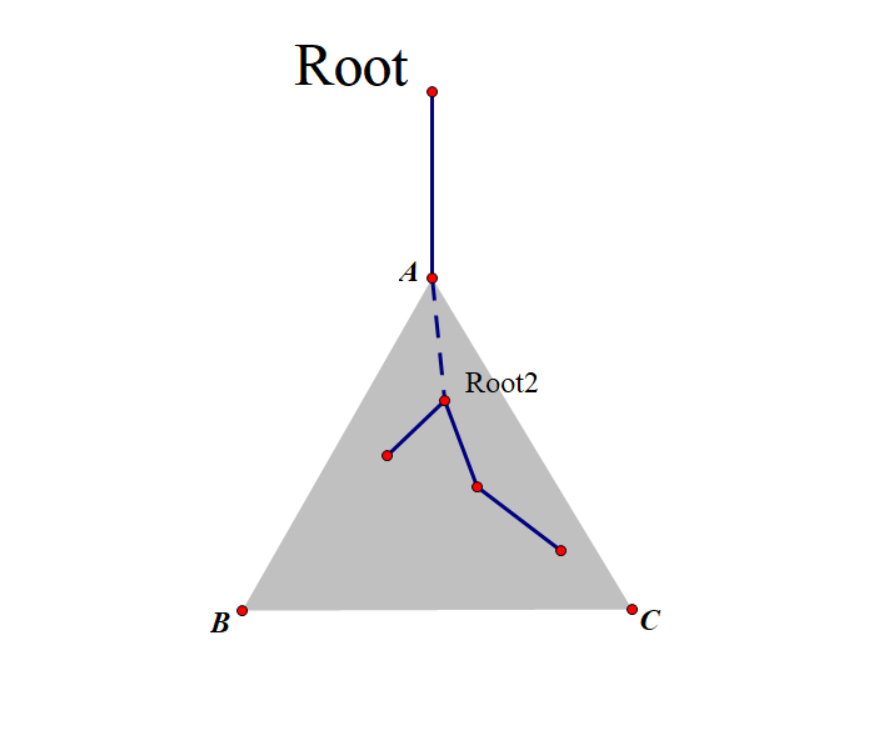
如图,Root 为根的子树中存在答案(蓝色实边路径),可以看成以 Root 为根的两棵子树存在答案,所以只用处理情况2就行了,可以用分治的方法,这是点分治的基本原理。
先从找好一个根开始。
过程
选根
首先根不能随便选,选根不同会影下面遍历的效率的,如图:
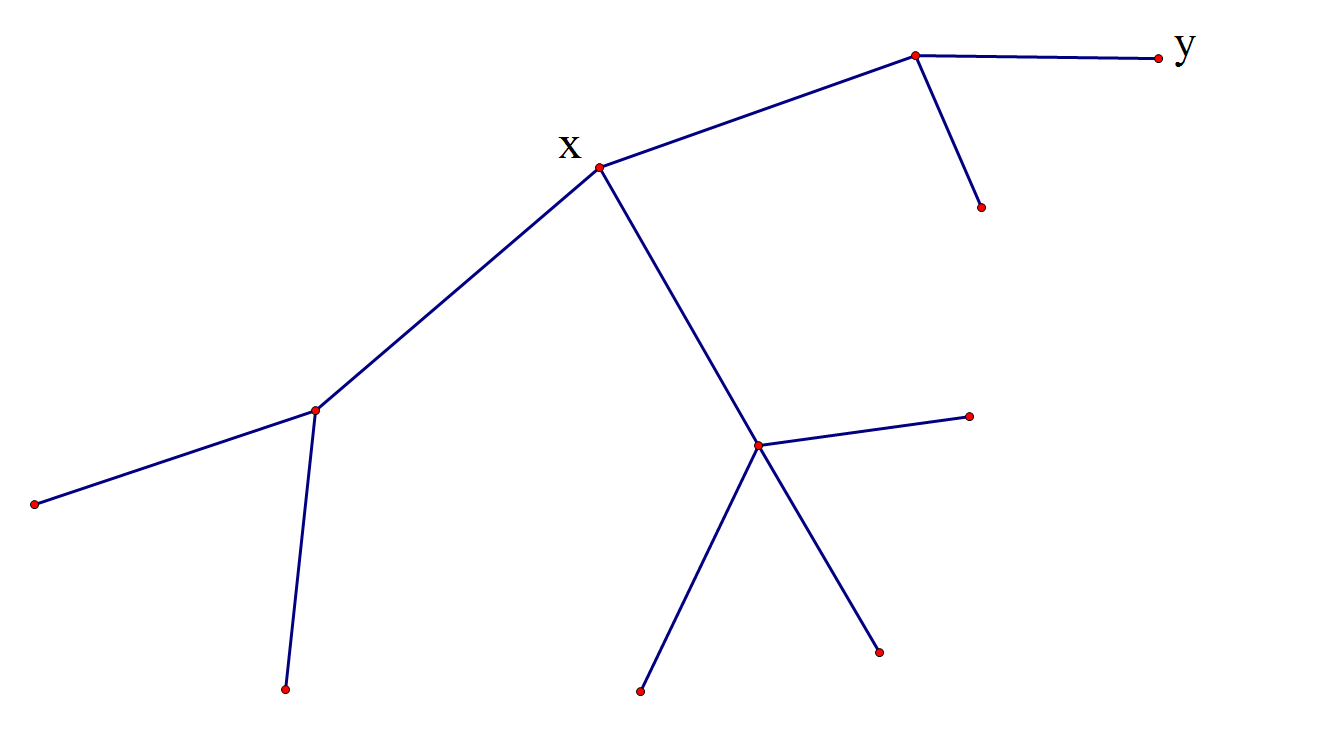
显然选 \(y\) 为根比选 \(x\) 为根不优,选 \(x\) 最多递归 \(2\) 层,选 \(y\) 最多递归 \(4\) 层。
可以发现找树的重心(重心所有的子树的大小都不超过整个树大小的一半)是最优的。
我们可以根据每个点子树大小确定根,当根的最大的子树最小时肯定是重心。
一个简单的树形 DP 就能搞定。
void getroot(int u,int fa) {
siz[u]=1,f[u]=0;
for(int i=head[u]; i; i=e[i].nxt) {
int v=e[i].to;
if(v==fa||vis[v]) {
continue;
}
getroot(v,u),siz[u]+=siz[v],f[u]=std::max(siz[v],f[u]);
}
f[u]=std::max(sum-siz[u],f[u]);
if(f[u]<f[r]) {
r=u;
}
}
因为之后的分治过程还需要对子树单独找重心,所以代码中有 \(vis\),但是开始对整棵树无影响。
求距离
找到根了,现在我们可以 dfs 一遍重心的子树,求出重心到子树各个点的距离。
然后可以枚举子树里的两个点,如果两个点到重心的距离和为 \(k\)(题目要找距离为 \(k\) 的点对),那么答案 \(+1\)。
这是第二种情况,第一种情况就让距离根为 \(k\) 的点跟重心配对就行了,因为重心到重心的距离为 \(0\)。
统计答案
肯定不能直接枚举啊……\(n^2\) 的复杂度啊!
考虑枚举一个点,另一个点可以通过二分来求解,sort 一下让距离有序,这样要找距离为 \(k\)——枚举点的距离的点的个数,因为相同距离的点现在是连续的,所以可以二分出左右边界\(l,r\),\(ans+=r-l+1\)。
也可以通过移动两个指针来实现只要不是枚举两个点就行了。
这样我们就快乐的A掉了这道题……了吗?
求一遍发现答案不对诶!似乎多了几种情况?如图: 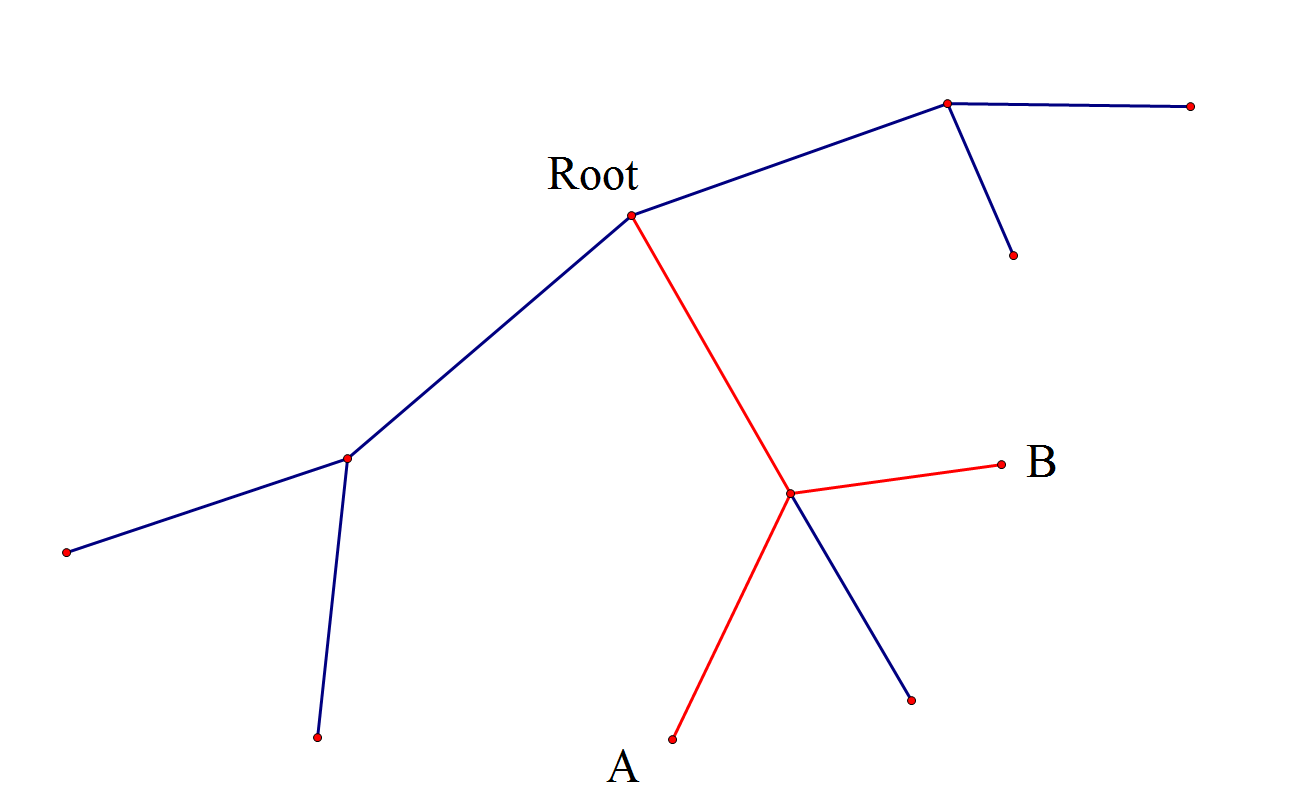
假设 \(k=4\),图中 \(A\) 到 Root 的距离为 \(2\),\(B\) 到 Root 的距离为 \(2\),合起来是 \(4\),这时候答案 \(+1\),但是显然这两个点最短路径不是 \(4\)!这是因为它们在同一子树中,到重心的路径有重叠部分。
这时要怎么处理呢?
- 可以求距离的时候把点染色,不同子树不同颜色,那么求答案的时候就得枚举每个符合答案的每个点看是否不在一个子树里。
- 可以求当前点儿子的答案,统计儿子答案时各个点的距离加上儿子到根的距离,即把符合在一个子树条件的情况统计出来,最后这个点的答案减去儿子答案就行了。
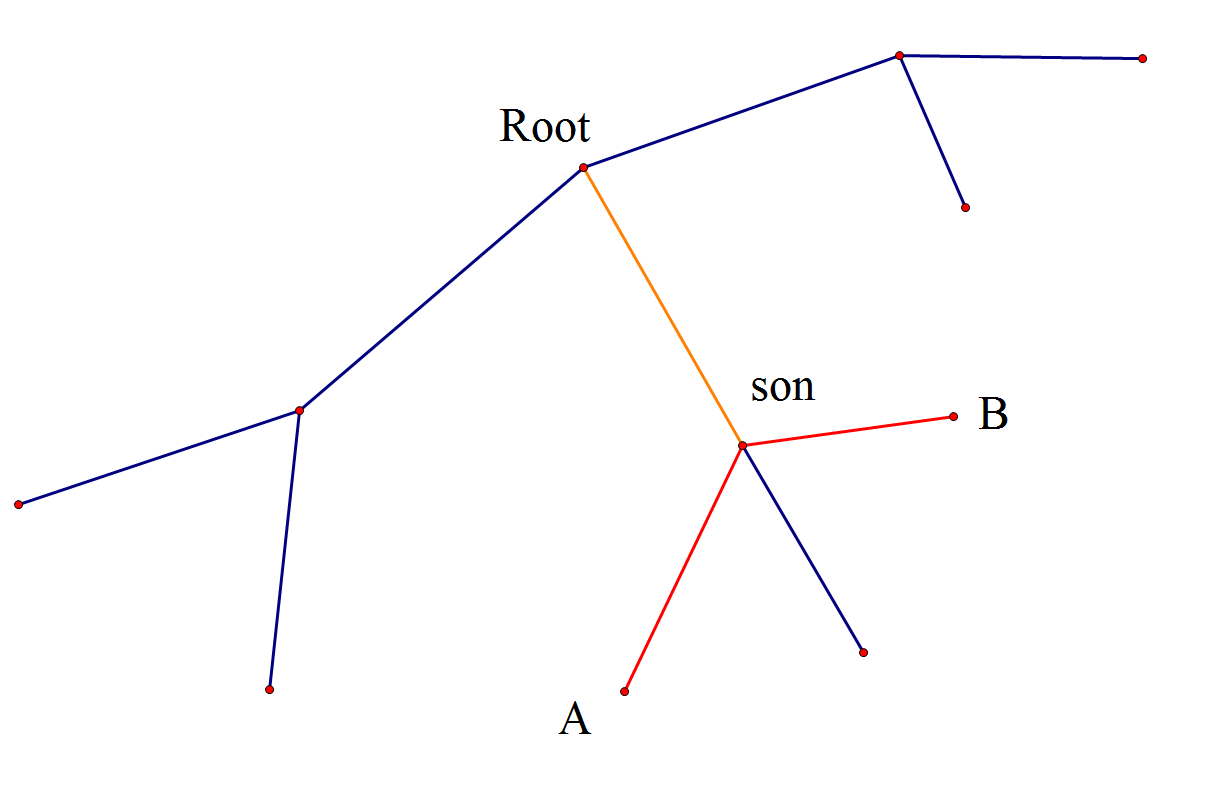
图中求 Root 儿子 son 的答案,因为加上儿子到重心的距离,所以 \(A\) 的距离还是 \(2\),\(B\) 的距离还是 \(2\),这样就把不符合条件的答案去掉了。
int cal(int u,int x) {
dis[u]=x,px[0]=0,getdis(u,u),std::sort(px+1,px+px[0]+1);
int temp=0;
for(int i=1,j=px[0]; i<j; ) {
if(px[i]+px[j]<=k) {
temp+=j-i++;
} else {
j--;
}
}
return temp;
}
void solve(int u) {
vis[u]=1,ans+=cal(u,0);
for(int i=head[u]; i; i=e[i].nxt) {
int v=e[i].to,w=e[i].w;
if(vis[v]) {
continue;
}
ans-=cal(v,w),r=0,sum=siz[v],getroot(v,u),solve(r);
}
}
这样答案就对了。
复杂度
每次处理找树的重心,保证递归层数不超过 \(\log n\),dfs 求距离复杂度是 \(O(n)\),这里处理答案是 \(\log n\),所以这个题总复杂度是 \(O(n\log^2 n)\)。
注意:因为有的题可以用桶排序,所以复杂度可以降到 \(O(\log n)\)。当然有的题桶开不下必须 sort。
推荐题
综合练习
- 【HAOI 2009】毛毛虫
- 【POI 2013】LUK-Triumphal arch
- 【CF 219D】Choosing Capital for Treeland
- 【ZJOI 2007】时态同步
- 【NOI2011】道路修建
- 【LG P5658】括号树
