https://blog.csdn.net/weixinhum/article/details/85059557
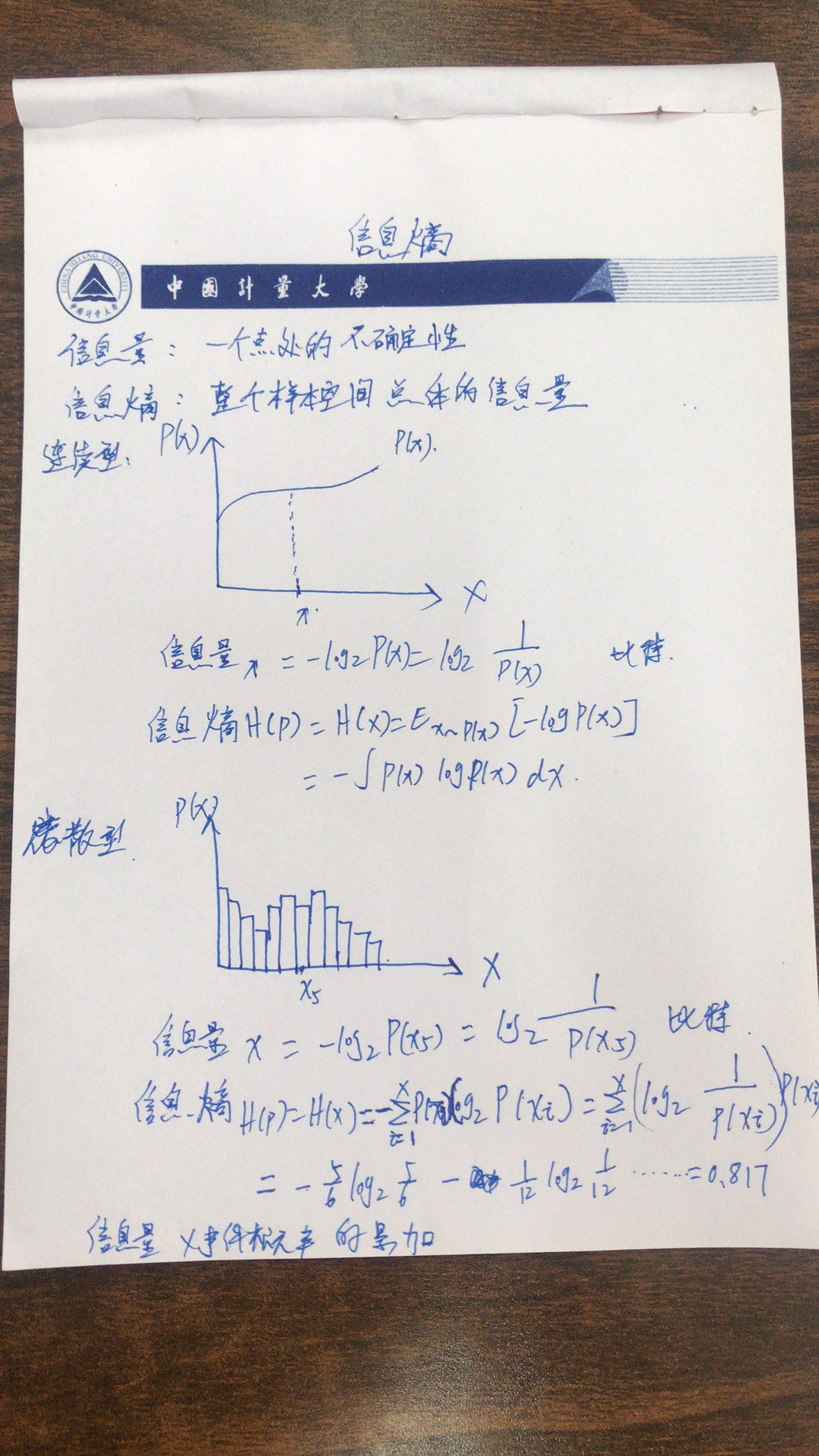
上一篇文章我们简单介绍了香农信息量的概念,由香农信息量我们可以知道对于一个已知概率的事件,我们需要多少的数据量能完整地把它表达清楚,不与外界产生歧义。但对于整个系统而言,其实我们更加关心的是表达系统整体所需要的信息量。比如我们上面举例的aaBaaaVaaaaa aaBaaaVaaaaaaaBaaaVaaaaa这段字母,虽然B BB和V VV的香农信息量比较大,但他们出现的次数明显要比a aa少很多,因此我们需要有一个方法来评估整体系统的信息量。
相信你可以很容易想到利用期望这个东西,因此评估的方法可以是:“事件香农信息量×事件概率”的累加。这也正是信息熵的概念。
如aaBaaaVaaaaa aaBaaaVaaaaaaaBaaaVaaaaa这段字母,信息熵为:−56log256−2×112log2112=0.817 -frac{5}{6}log_2frac{5}{6}-2×frac{1}{12}log_2frac{1}{12}=0.817−
6
5
log
2
6
5
−2×
12
1
log
2
12
1
=0.817
abBcdeVfhgim abBcdeVfhgimabBcdeVfhgim这段字母,信息熵为:−12×112log2112=3.585 -12×frac{1}{12}log_2frac{1}{12}=3.585−12×
12
1
log
2
12
1
=3.585
从数值上可以很直观地看出,第二段字母信息量大,和观察相一致。
对于连续型随机变量,信息熵公式变为积分的形式,如下:
H(p)=H(X)=Ex∼p(x)[−logp(x)]=−∫p(x)logp(x)dx H ( p ) = H ( X ) = mathrm { E } _ { x sim p ( x ) } [ - log p ( x ) ] = - int p ( x ) log p ( x ) d xH(p)=H(X)=E
x∼p(x)
[−logp(x)]=−∫p(x)logp(x)dx
刚才定义了随机变量在一个点处的香农信息量,那么如何衡量随机变量X(或整个样本空间)的总体香农信息量呢?下面就要引出随机变量X的信息熵的概念,或概率分布p的信息熵。信息熵H(p)是香农信息量-logp(x)的数学期望,即所有X=x处的香农信息量的和,由于每一个x的出现概率不一样(用概率密度函数值p(x)衡量),需要用p(x)加权求和。因此信息熵是用于刻画消除随机变量X的不确定性所需要的总体信息量的大小。其数学定义如下:
对于离散型随机变量,信息熵公式如下:
H(p)=H(X)=Ex∼p(x)[−logp(x)]=−∑ni=1p(x)logp(x) H ( p ) = H ( X ) = mathrm { E } _ { x sim p ( x ) } [ - log p ( x ) ] = -sum_{i=1}^n p ( x )log p ( x )
H(p)=H(X)=E
x∼p(x)
[−logp(x)]=−
i=1
∑
n
p(x)logp(x)
对于连续型随机变量,信息熵公式如下:
H(p)=H(X)=Ex∼p(x)[−logp(x)]=−∫p(x)logp(x)dx H ( p ) = H ( X ) = mathrm { E } _ { x sim p ( x ) } [ - log p ( x ) ] = - int p ( x ) log p ( x ) d x
H(p)=H(X)=E
x∼p(x)
[−logp(x)]=−∫p(x)logp(x)dx
注意,我们前面在说明的时候log loglog是以2为底的,但是一般情况下在神经网络中,默认以e ee为底,这样算出来的香农信息量虽然不是最小的可用于完整表示事件的比特数,但对于信息熵的含义来说是区别不大的。其实只要这个底数是大于1的,都能用来表达信息熵的大小。