matlab做隐函数的等值(高)线&等值面

可恶的毕设涉及到做出2维及3维空间上隐函数的等值面(线)图

2维，3维的目的都一样，就是做出隐函数表示的结构图，将函数值为0的点视为表面并显示出来，然后计算等值线(面)所围之外的面积(体积)占整个空间的面积(体积)的百分比。

一.2维平面隐函数等值线

2维平面上的等值线图使用contourf函数就可以实现。应该也有许多其他方法。

使用函数 (z=cos(x)*cos(y)+0.5)

1. 做出带填充的等值(高)线图

clear all;
clc;
% 给出定义域，生成网格。
x = 0:0.01:2*pi;
y = 0:0.01:2*pi;
[X, Y] = meshgrid(x, y);

% 给出隐函数表达式
Z = cos(X).*cos(Y)+0.5;

% 做等值线图
ax = figure;
[M, C] = contourf(X, Y, Z);
axis off;

C.LineWidth = 1;
C.ShowText = 'on';

生成的图像为：

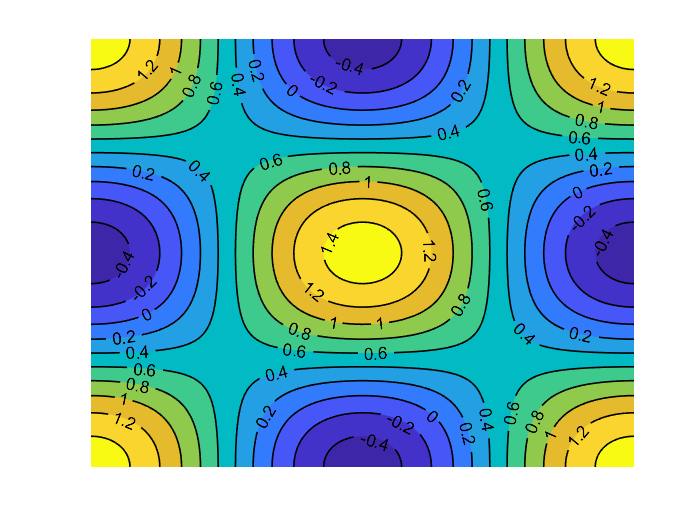
根据二元函数求极值的方法，(frac{partial f}{partial x})，(frac{partial f}{partial y})都等于0，且(frac{partial^2 f}{partial x^2}frac{partial^2 f}{partial y^2} - (frac{partial^2 f}{partial x partial y})^2 > 0)，则x,y为函数极值点，若(frac{partial^2 f}{partial x^2}和frac{partial^2 f}{partial y^2})都大于0，则为极小值，都小于0，则为极大值。
求出函数的极大值点分别为(0, 0)、(left(pi,pi ight))，函数值为1.5。极小值点分别为(0, (pi))、((pi), 0)，函数值为-0.5。
从图像上可以看出极大值与极小值点，且函数在x,y上的周期均为(2pi)。

2. 做出函数值为0的带填充等值(高)线

修改上面调用contourf的形式，顺便把ShowText关掉。

...
[M, C] = contourf(X, Y, Z, [0, 0]);
...
C.ShowText = 'off';

得到的图像为：

上面的图像在边界上并没有做出等高线，因此，使用max函数为图像增加边界。

...
% 给出隐函数表达式
Z = max(max(cos(X).*cos(Y)+0.5, X.*(X-2*pi+0.01)), ...
    Y.*(Y-2*pi+0.01));
...

之后做出的图像为：

之所以使用(X.*(X-2*pi+0.01))与(Y.*(Y-2*pi+0.01))，是因为使用2pi时无法做出边界，原因可能是matlab作图时是按照类似的坐闭右开区间绘制的，因此把X,Y减小0.01。

还有一个问题是填充问题，我想实现的是等高线内部填充，而不是外部填充。
查了半天也没找到办法，通过colormap设置颜色梯度，里面永远是白色，如下图。

map = [0 0 0;
        1 1 1];
colormap(ax, map);

得到的图像为：

最后才发现，colormap填充的是等值线之间的图像，因为我只画了一条(z=0)的等值线，所以只能填充等值线以外的。
只要指定一个小于二元函数最小值的值以及所需的值，如下取[-0.5, 0]，使用colormap进行内部填充，-0.5为函数最小值。
修改代码为：

...
[M, C] = contourf(X, Y, Z ,[-0.5, 0]);    % 因为最小值为-0.5
axis off;
...
map = [0, 0.6, 1;
        1, 1, 1];
colormap(ax, map);

得到图像：

3. 得到等高线外部占全部面积的百分比

因为使用的离散数据，将大于0的所有节点求和，并除以所有节点即近似为空隙所占面积的百分比。

...
lenX = length(x);
lenY = length(y);
tot = lenX * lenY;
num_in_con = 0;
for i=1:1:lenX
    for j=1:1:lenY
        if (Z(i, j) > 0)
            num_in_con = num_in_con + 1;
        end
    end
end

per = num_in_con / tot;

求得结果为per=0.8160;

二. 3维隐函数等值面

3维的隐函数等值面使用函数isosurface()、patch()以及isonormals()。
以三元函数(f = (x^2+(frac{9}{4}*y^2+sqrt{z}^3-x^2*z^3-frac{9}{80}*y^2*z^3)为例，程序如下:

clear all;
clc

x = -10:0.05:10;
y = -10:0.05:10;
z = -10:0.05:10;

[X, Y, Z] = meshgrid(x, y, z);

f = (X.^2+(9/4)*Y.^2+Z.^2-1).^3-X.^2.*Z.^3-(9/80).*Y.^2.*Z.^3;

h = patch(isosurface(X, Y, Z, f, 0));
isonormals(X, Y, Z, f, h);

% 设置图像属性
h.FaceColor = 'red';
h.EdgeColor = 'none';
alpha(1);
view([1, 1, 1]);
axis equal;
axis off;
camlight('right');
lighting gouraud;
xlabel('x'); ylabel('y'); zlabel('z');

其中isosurface(X,Y,Z,f,0);获取隐函数的等值面，返回包含面和顶点的结构体，这里的面指的是构成隐函数曲面的三角面片，而顶点即为三角形的三个顶点。
patch()由包含面和顶点的结构体绘制隐函数图,返回h为Patch属性，可以使用h改变图像外观。结果图如下：

isonormals()基于函数值从新计算等值面的法向量，否则图像不准确，不使用isonormals()函数的图像如下：