zoukankan      html  css  js  c++  java

  • 结对项目-四则算式自动生成器

    目录

    结对学号：3118005118 3118005113

    项目仓库：https://amzz.coding.net/p/CalculationMaker/d/CalculationMaker/git

    需求分析(共10个)

    生成题目

    1. 使用 -n 参数控制生成题目的个数，例如

      Myapp.exe -n 10

      将生成10个题目。

    2. 使用 -r 参数控制题目中数值（自然数、真分数和真分数分母）的范围，例如

      Myapp.exe -r 10

      将生成10以内（不包括10）的四则运算题目。该参数可以设置为1或其他自然数。该参数必须给定，否则程序报错并给出帮助信息。

    检测题目

    1. 生成的题目中计算过程不能产生负数，也就是说算术表达式中如果存在形如e1− e2的子表达式，那么e1≥ e2。

    2. 生成的题目中如果存在形如e1÷ e2的子表达式，那么其结果应是真分数，除号用的是÷ 。

    3. 每道题目中出现的运算符个数不超过3个。

    4. 程序一次运行生成的题目不能重复，即任何两道题目不能通过有限次交换+和×左右的算术表达式变换为同一道题目。

      例如，23 + 45 = 和45 + 23 = 是重复的题目，6 × 8 = 和8 × 6 = 也是重复的题目。3+(2+1)和1+2+3这两个题目是重复的，由于+是左结合的，1+2+3等价于(1+2)+3，也就是3+(1+2)，也就是3+(2+1)。但是1+2+3和3+2+1是不重复的两道题，因为1+2+3等价于(1+2)+3，而3+2+1等价于(3+2)+1，它们之间不能通过有限次交换变成同一个题目。

    保存题目和计算

    1. 生成的题目存入执行程序的当前目录下的Exercises.txt文件，格式如下：

      1.四则运算题目1

      2.四则运算题目2

    2. 计算出所有题目的答案，并存入执行程序的当前目录下的Answers.txt文件，格式如下：
      1.答案1

      2.答案2

    3. 程序应能支持一万道题目的生成。

    4. 程序支持对给定的题目文件和答案文件，判定答案中的对错并进行数量统计，输入参数如下：

      Myapp.exe -e .txt -a .txt

      统计结果输出到文件Grade.txt，格式如下：

      Correct: 5 (1, 3, 5, 7, 9)

      Wrong: 5 (2, 4, 6, 8, 10)

      其中“:”后面的数字5表示对/错的题目的数量，括号内的是对/错题目的编号。为简单起见，假设输入的题目都是按照顺序编号的符合规范的题目。

    思路分析

    算式重复问题

    1.初步方案

    基本思路

    ​ 第一反应就是用ID来匹配题目，每一个题目配有一个独立的ID，解决重复时比较ID即可。
    ​ 然后就是如何用题目的ID如何匹配的问题了。
    ​ 题目的不同，本质上是树的结构不同。
    ​ 想法是用二叉树，那么题目的生成就可以抽象为：生成一棵计算符树的结构，填入计算符，然后根据需求填满数字（如减法可以在生成数字的时候比较左右子树的结果，如果右字数大于左子树，左右子树调换，之类的）。

    树结构的规则协定

    ​ 由于加法和乘法有交换律，所以树的结构必须要有规则（比如左子树要大于右子树之类的）
    ​ 规则暂时还没想好= =，这个规则对不重复的意义很大，要考虑周全
    输出的时候，设置一个方法，由树输出算式时，加法和乘法左右子树可以交换输出，但内部存储必须要有规则。

    ID生成方案一（臭气冲天）

    ​ 由于最多只能有三个运算符，所以能生成的计算符树就就很有限了，一共有8种形状（1个运算符1种，2个运算符2种，3个运算符5种）

    算式生成方式一

    ​ 随机数0-7，生成结构树，0-3塞入运算符，再根据规则有限制地塞入数字（具体怎么塞，得慢慢考虑）

    算式生成方式二

    ​ 结构树和运算符塞入方式与一相同，而数字随机放入，再根据规则调整树的结构（基于左右子树调换），调整完成后再根据当前树的结构确定树结构的序号（哇，臭！）

    ​ 所以最后记录的东西有：树结构的序号，中序遍历计算符的编号，中序遍历叶子节点数据

    ID生成方案二（可 拓 展 性）

    1. 可以自动生成n个运算符的树

    2. 生成一个n+1个节点的数组

    3. 随机选择一种计算符，随机抽取两个数组中的节点，根据规则构成新的节点

    4. 在数组中删除2中选择到的两个节点，添加新的节点

    5. 若数组中有大于1个节点，回到2；若剩下一个节点，树生成完毕

      有一种方式可以用数组记录整棵二叉树的
      所以最后记录的东西有：运算符的个数，上述的数组，中序遍历计算符的编号，中序遍历叶子节点数据。

    2.终极方案

    ​ 确定用算式树来作为主体，在处理算式重复比较时，进行两层筛选，从根节点往下比较

    ​ 1.如果所含符号不同或数字不同，则直接判断不同

    ​ 2.如果该节点相同，对应比较或交叉比较其孩子相同，则继续比较其孩子的左右孩子

    效率分析

    生成方式

    1. 如果事先把所有情况都遍历出来，然后生成数字，按序号输出第i个算式，那应该是最快的。所以可以先写一个遍历程序，将所有情况写进txt，再随机输出，但这样如果要求远小于10000道的话，效率反而低了
    2. 如果在操作数随机生成时，尽可能先把取值范围缩小，从小范围生成随机数并观察是否满足不重复算式数，若不满足再扩大范围，可以缩短较大数计算时的延迟
    3. 分数在计算时比单纯整数速度慢，生成也比纯整数慢，所以可以人为控制生成含分数算式的频率来提高效率

    结构效率分析

    可以分为：1. 直接生成算式字符串 2. 节点随机生成组合成树 3.使用堆结构，用数组模拟树

    数据类型 遍历效率 生成效率 可扩展性 内存消耗 对比效率
    树 低 低 高 中 高
    堆(数组模拟树) 高 中 中 高 中
    字符串 中 高 低 低 低

    操作数

    1. 将整数和分数相结合成为一个类，统称为分数类

    2. 该类带有整数部分，分子部分，分母部分

    3. 需要重载运算符+-*/

    程序设计

    类设计

    1. 文件IO FileIO

      • 读取文件
      • 输出保存文件
      • 获得cmd处于位置并合成文件路径
      • 检查当前路径下是否存在文件

    2. 指令处理 CommandChecker

      • 错误处理
      • 指令检查及运行

    3. 算式处理 CalculationIO

      • 算式读取
      • 算式输出
      • 答案读取
      • 答案输出

    4. 算式树节点 Calculation

      class CalculationNode
{
	#region members
	public OperatorType oprtType;		//操作符
	public Fraction fraction;			//操作数	
	public CalculationNode leftChild;	//左孩子
	 CalculationNode rightChild;	//右孩子
	#endregion members
	。。。。。。
}
      • 成员：分数+操作符类型+左右孩子
      • 操作符优先级比较
      • ToString()

    5. 算式树Calculation

      class Calculation
{
	#region members
	/// <summary>
	/// 算式树(数组-堆)
	/// </summary>
	public CalculationNode RootNode ;

	Stack<Node> s;//操作符
	Stack<Node> s1;//操作数
	Stack<Node> q;//后缀表达式倒数//前缀表达式
	#endregion members
	。。。。。。
}
      • 从算式字符串到算式树的构造函数
      • 从算式树到算式字符串的转化函数
      • 计算算式树结果的成员函数
      • 随机生成算式构造函数
      • ToString()
      • 重载==,!=,Equals
      • 比较算式树是否相同的成员函数

    6. 算式管理器 CalculationManager

      • 已生成算式的List
      • 随机参数生成器（分数，数字，运算符）
      • 传入字符串检查器

    7. 主进程 Program

      class Program
{
	static void Main(string[] args)
	{
		CommandChecker.Run(args);
		Console.ReadKey();
	}
}

    结构体设计

    1. 分数结构体Fraction

      struct Fraction
{
	#region members
	/// <summary>
	/// 分子
	/// </summary>
	public int numerator;
	/// <summary>
	/// 分母
	/// </summary>
	public int denominator;
	/// <summary>
	/// 整数部分
	/// </summary>
	public int intPart;
	#endregion members
	......
}
      • 分子+分母+整数部分
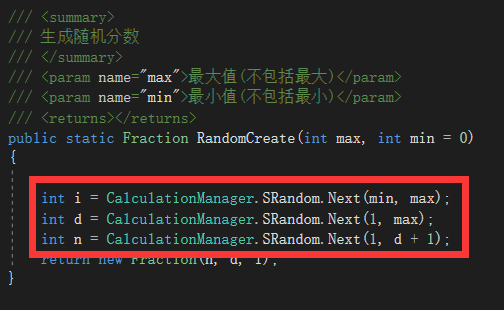
      • 生成随机分数
      • 字符串构造
      • 判断字符串可否转化为分数（包括可转化为整数）
      • 转化为标准分数
      • ToString()
      • 重载运算符+-*/，以及比较符==和!=

    2. 操作符类型 OperatorType

      public enum OperatorType
{
	None,
	Addition,
	Subtraction,
	Multiplication,
	Division
}

    3. 简化版节点(用于栈)

      struct Node
{
	public Fraction num;//操作数
	public char oper;//操作符
	public bool judge;//true表示操作数，false表示操作符
}

    4. 操作符优先级

      public enum priority
{
	lower,
	same,
	higher
}

    重要成员函数

    1. 比较算式树
    /// <summary>
/// 比较算式树
/// </summary>
/// 1.如果所含符号不同或数字不同，则直接不同(暂时舍弃第一层筛选，感觉没必要)
/// 2.如果该节点相同，对应比较或交叉比较其孩子相同，则继续比较左右孩子
/// <returns></returns>
private static bool CompareTo(CalculationNode c1,CalculationNode c2)
{
	if(c1.isOperator) 
	{
		if(c1.oprtType == c2.oprtType)
		{
			return(CompareTo(c1.leftChild, c2.leftChild) && CompareTo(c1.rightChild, c2.rightChild)|| CompareTo(c1.leftChild, c2.rightChild) && CompareTo(c1.rightChild, c2.leftChild));
         }
         else
         {
              return false;
         }
	}
	else 
	{
		if (c1.fraction == c2.fraction)
		{
			return true;
		}
		else
		{
			return false;
		}        
	}
}

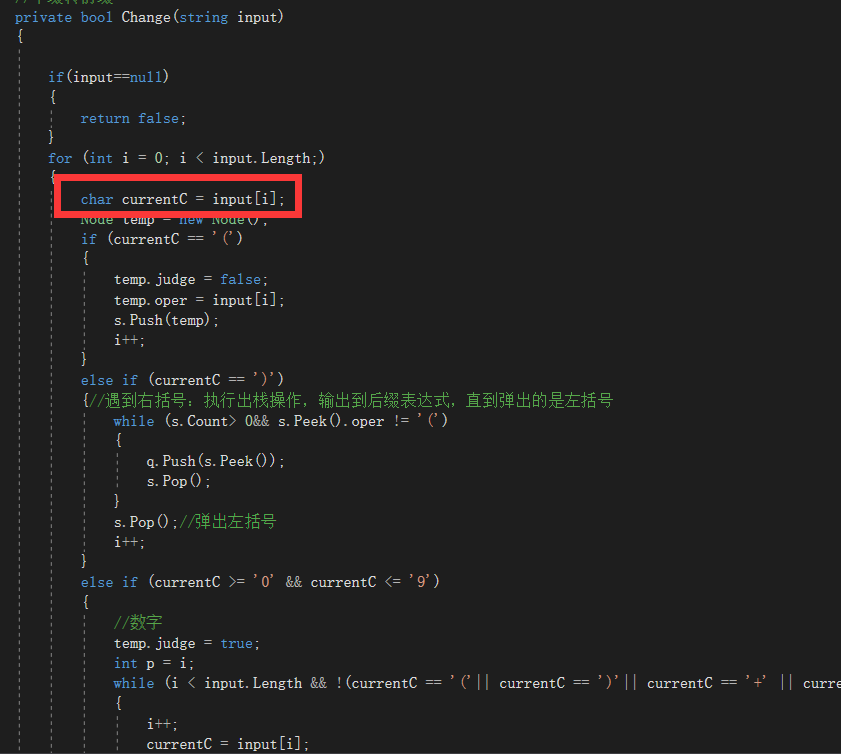
    1. 中缀转前缀

      /// <summary>
/// 字符串转换算式(构造函数)
/// </summary>
/// <param name="s">字符串</param>
/// <param name="cal">算式</param>
/// <returns>是否可以构造</returns>
public static bool CreateFromString(string temp, out Calculation cal)
{
	cal = new Calculation(); 
	if(!cal.Change(temp))           //1.中缀转前缀
	{
		return false;
	}
	Stack<Node> q=new Stack<Node>();
	while (cal.q.Count>0)               
	{
		q.Push(cal.q.Peek());
		cal.q.Pop();
	}

	Stack<CalculationNode> s=new Stack<CalculationNode>();
	CalculationNode now;
	CalculationNode then;
	if (q.Count<=0)
	{
		return false;
	}
	while (q.Count >0)
	{
		if (q.Peek().judge)
		{
			now = new CalculationNode (CalculationNode.charToOperatorType(q.Peek().oper),q.Peek().num);
			s.Push(now);
			q.Pop();
		}
		else if (!q.Peek().judge)
		{
			now = s.Peek();
			s.Pop();
             then = s.Peek();
             s.Pop();
             now = new CalculationNode (CalculationNode.charToOperatorType(q.Peek().oper), q.Peek().num, then, now );
             s.Push(now);
             q.Pop();
		}
}
	cal.RootNode = s.Peek();
	while (s.Count>0)
		s.Pop();
	return true;
}

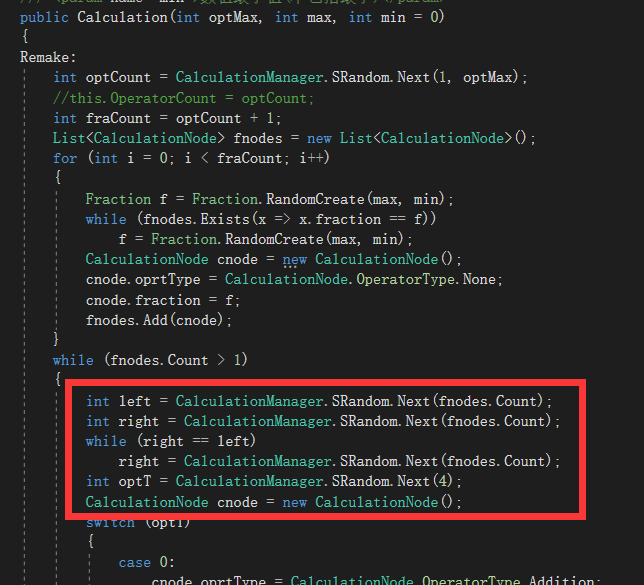
    2. 随机生成算式构造函数

      /// <summary>
/// 随机生成算式构造函数
/// </summary>
/// <param name="optMax">运算符最大数量</param>
/// <param name="max">数值最大值(不包括最大)</param>
/// <param name="min">数值最小值(不包括最小)</param>
public Calculation(int optMax, int max, int min = 0)
{
Remake:
	int optCount = CalculationManager.SRandom.Next(1, optMax + 1);
	int fraCount = optCount + 1;
	List<CalculationNode> fnodes = new List<CalculationNode>();
	for (int i = 0; i < fraCount; i++)
	{
    	Fraction f = Fraction.RandomCreate(max, min);
     	while (fnodes.Exists(x => x.fraction == f))
     	f = Fraction.RandomCreate(max, min);
     	CalculationNode cnode = new CalculationNode();
     	cnode.oprtType = CalculationNode.OperatorType.None;
     	cnode.fraction = f;
     	fnodes.Add(cnode);
      }
      while (fnodes.Count > 1)
      {
         int left = CalculationManager.SRandom.Next(fnodes.Count);
         int right = CalculationManager.SRandom.Next(fnodes.Count);
         while (right == left)
         right = CalculationManager.SRandom.Next(fnodes.Count);
         int optT = CalculationManager.SRandom.Next(4);
         CalculationNode cnode = new CalculationNode();
         switch (optT)
         {
         case 0:
             cnode.oprtType = CalculationNode.OperatorType.Addition;
             break;
         case 1:
             cnode.oprtType = CalculationNode.OperatorType.Subtraction;
             if (fnodes[left].Calculate() < fnodes[right].Calculate())
             {
                  int t = left;
                  left = right;
                  right = t;
              }
              break;
          case 2:
              cnode.oprtType = CalculationNode.OperatorType.Multiplication;
              break;
          case 3:
              if (fnodes[right].Calculate() == Fraction.zero)
              {
                   if (fnodes[left].Calculate() == Fraction.zero)
                   goto Remake;    //没救了，重开一个
                   else
                   {
                       int t = left;
                       left = right;
                       right = t;
                    }
               }
               cnode.oprtType = CalculationNode.OperatorType.Division;
               break;
          }
          cnode.leftChild = fnodes[left];
          cnode.rightChild = fnodes[right];
          fnodes[left] = cnode;
          fnodes.RemoveAt(right);
      }
      this.RootNode = fnodes[0];
}

    模块测试

    1. -n 与 -r 指令

    打开cmd，输入如下指令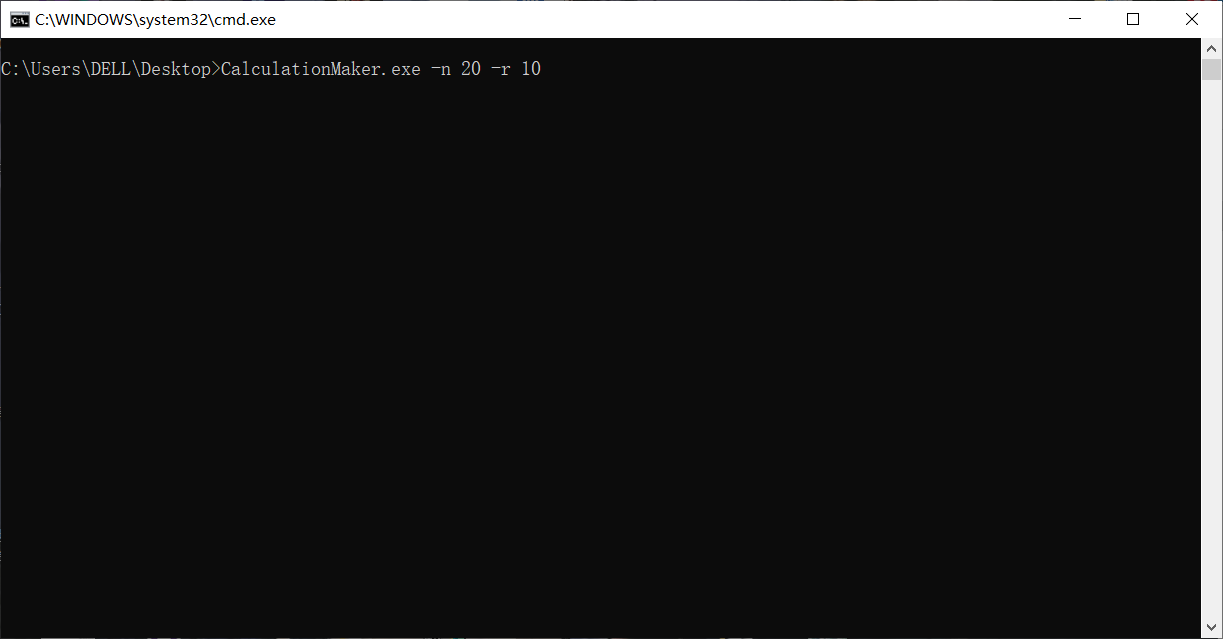G1PfZn.png键入回车，输出如图
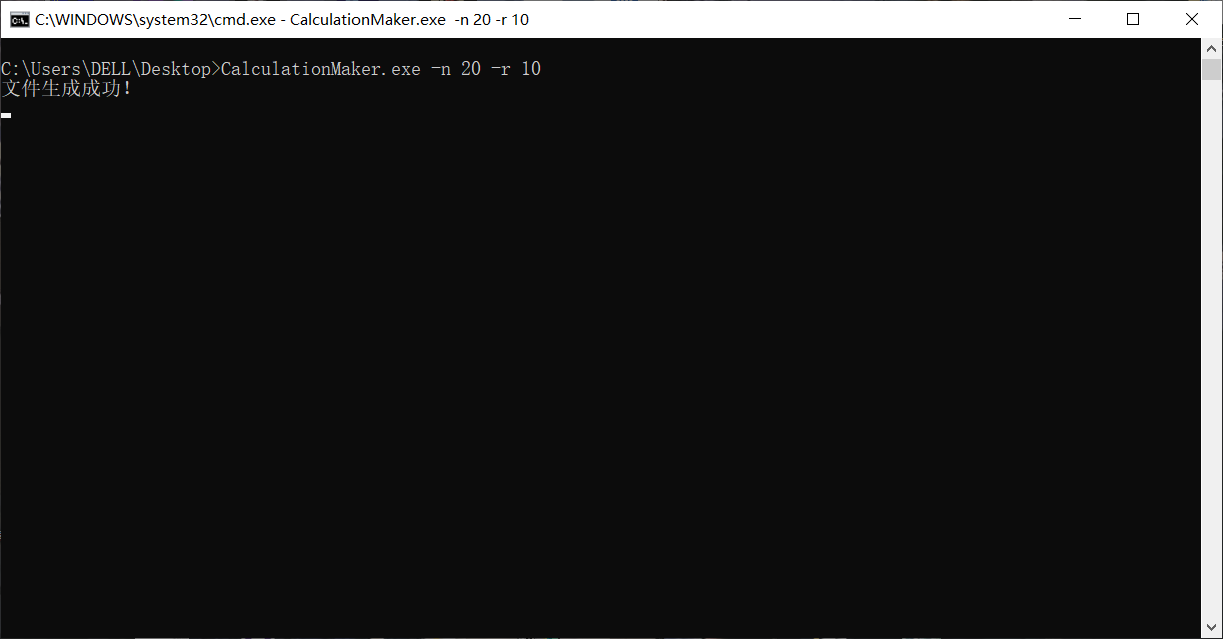
    G1Phaq.png
    同时在运行文件夹（这里是桌面），出现了两个文件
    G1PRqs.png
    打开两个文件，内容如图，符合预期
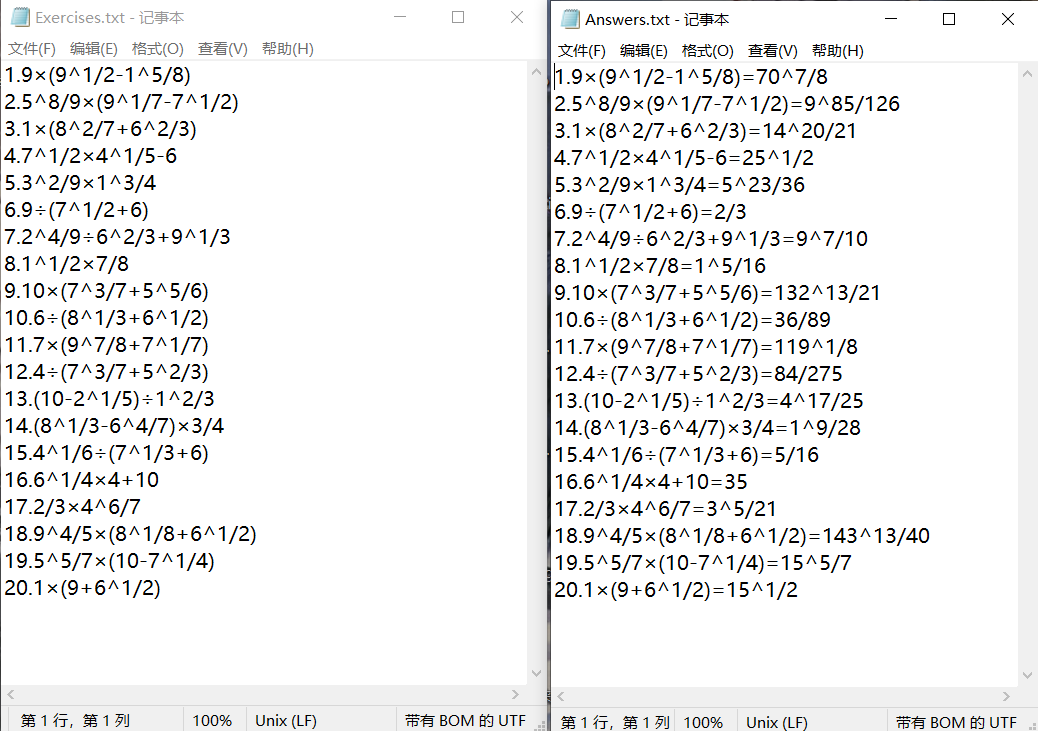
    G1P4I0.png

    2. -e 与 -a 指令

    这里我们用上一步生成的文件稍作修改作测试样例
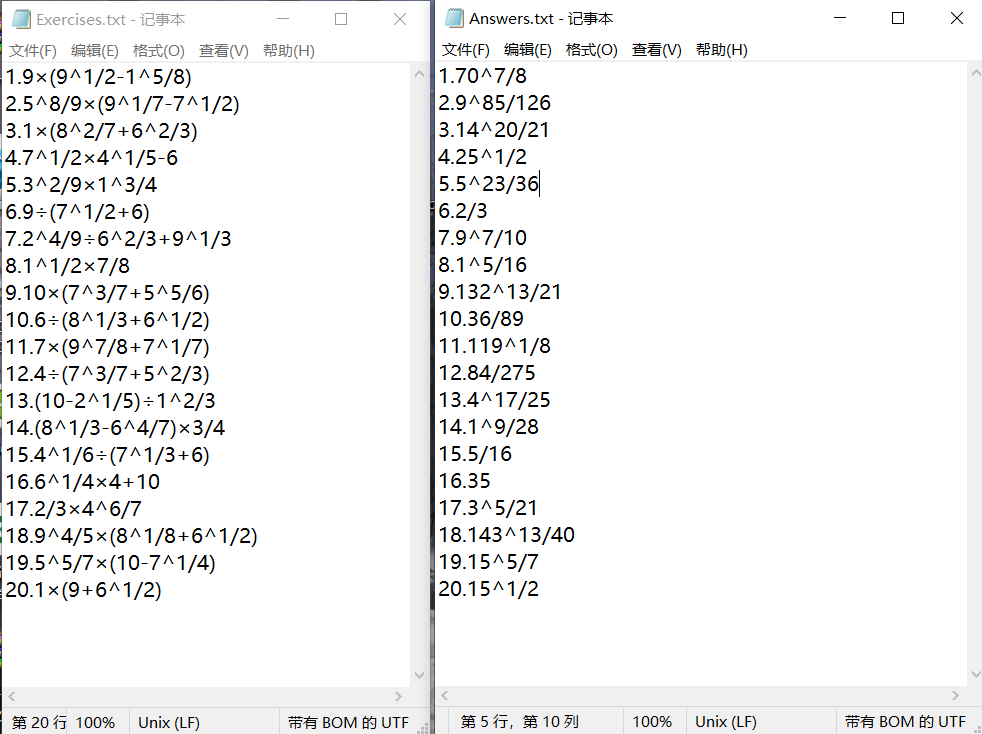
    G1iwy4.png
    打开cmd，输入如下指令
    G1iNWT.png
    键入回车，输入如图
    G1iaSU.png
    同时在运行文件夹（这里是桌面），出现了Grade.txt文件
    G1iYF0.png
    打开，内容如图，符合预期
    G1itYV.png
    我们对答案稍作修改，再次测试
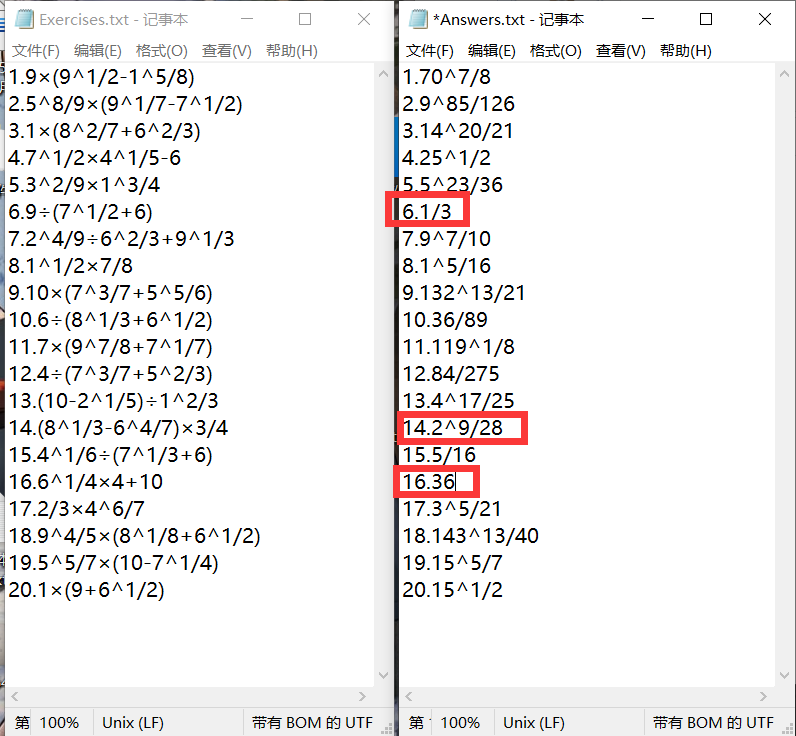
    G1irwR.png
    在cmd再次运行，结果如图
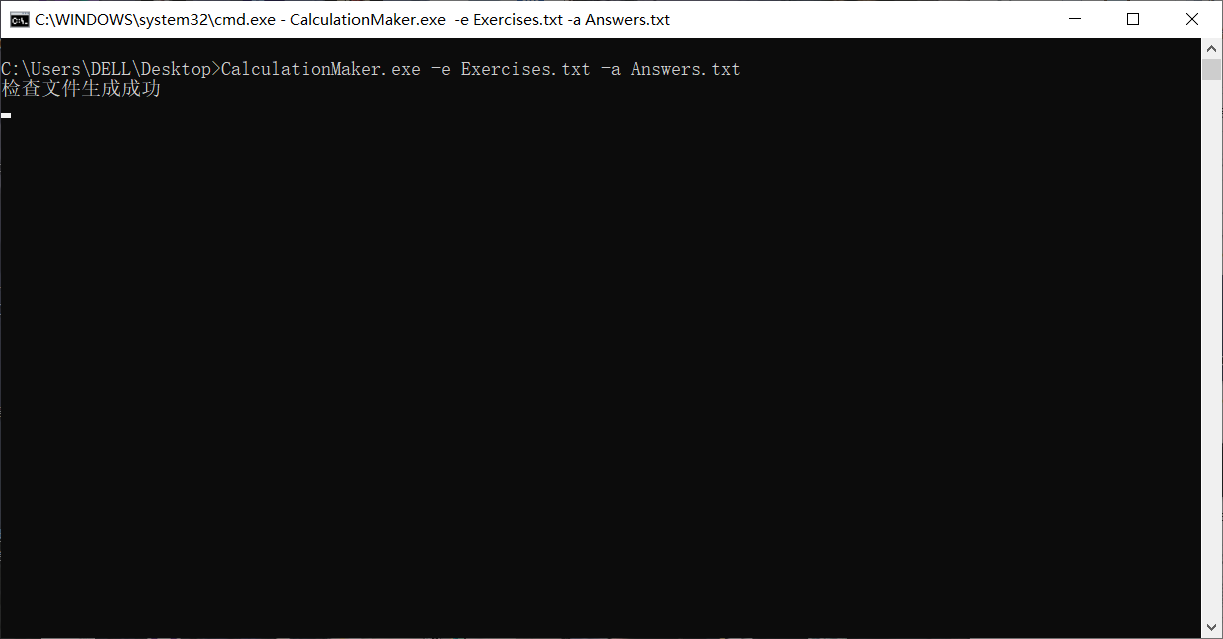
    G1isT1.png
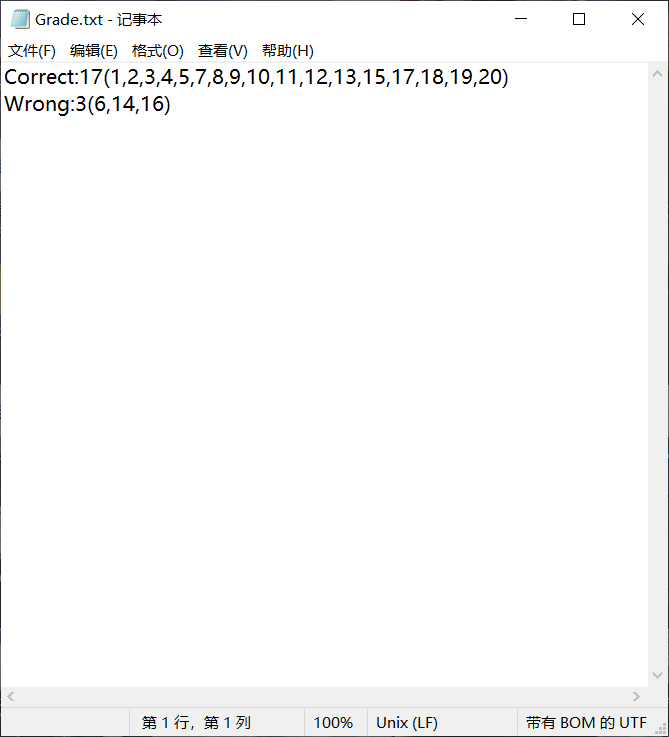
    这里我们设计将原Grade.txt覆盖，现Grade.txt如图，符合预期
    G1icY6.png

    性能优化及测试

    测试准备

    1. 增加计时器，用于计算运行时间
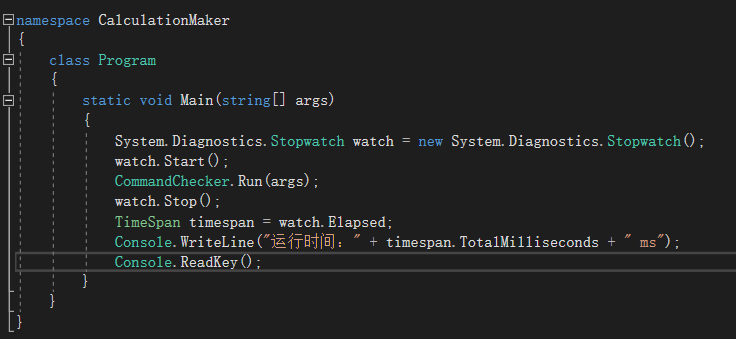
      G1Uq6U.png
    2. 增加生成报数，防止卡死，并能直观感受速度
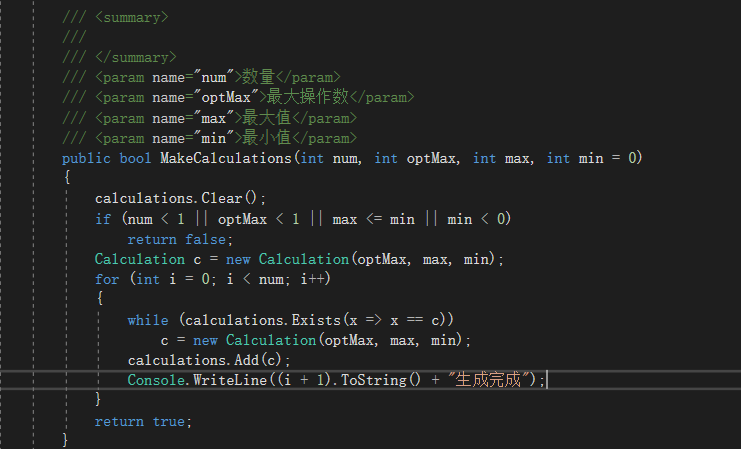
      G1Uj0J.png

    优化前

    先来生成1000个试试水，一口吃不成个胖子
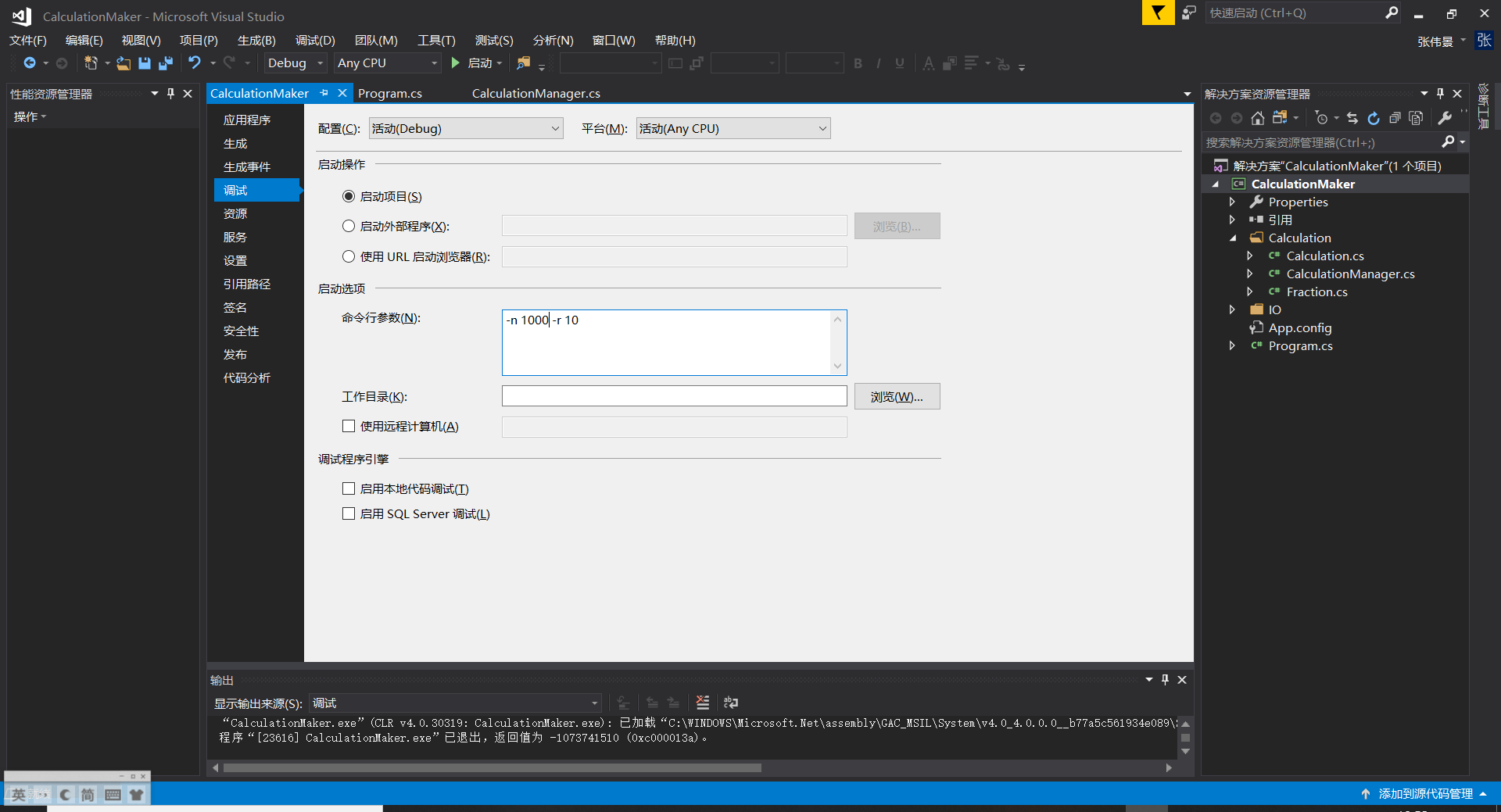
    G1aCp6.png
    发现是真的慢，1000个就要9w+ ms，生成1w要得10倍以上
    G1aSt1.png

    进行优化

    因为程序运行本来就慢，性能检测就更慢了，所以就根据经验进行优化

    发现问题

    1. 引索器
      这个可以说是老问题了，上一次项目就发现过这样的问题：
      当样本过大时，List.Count，以及Array[index]等操作的时间就是需要考虑的事了
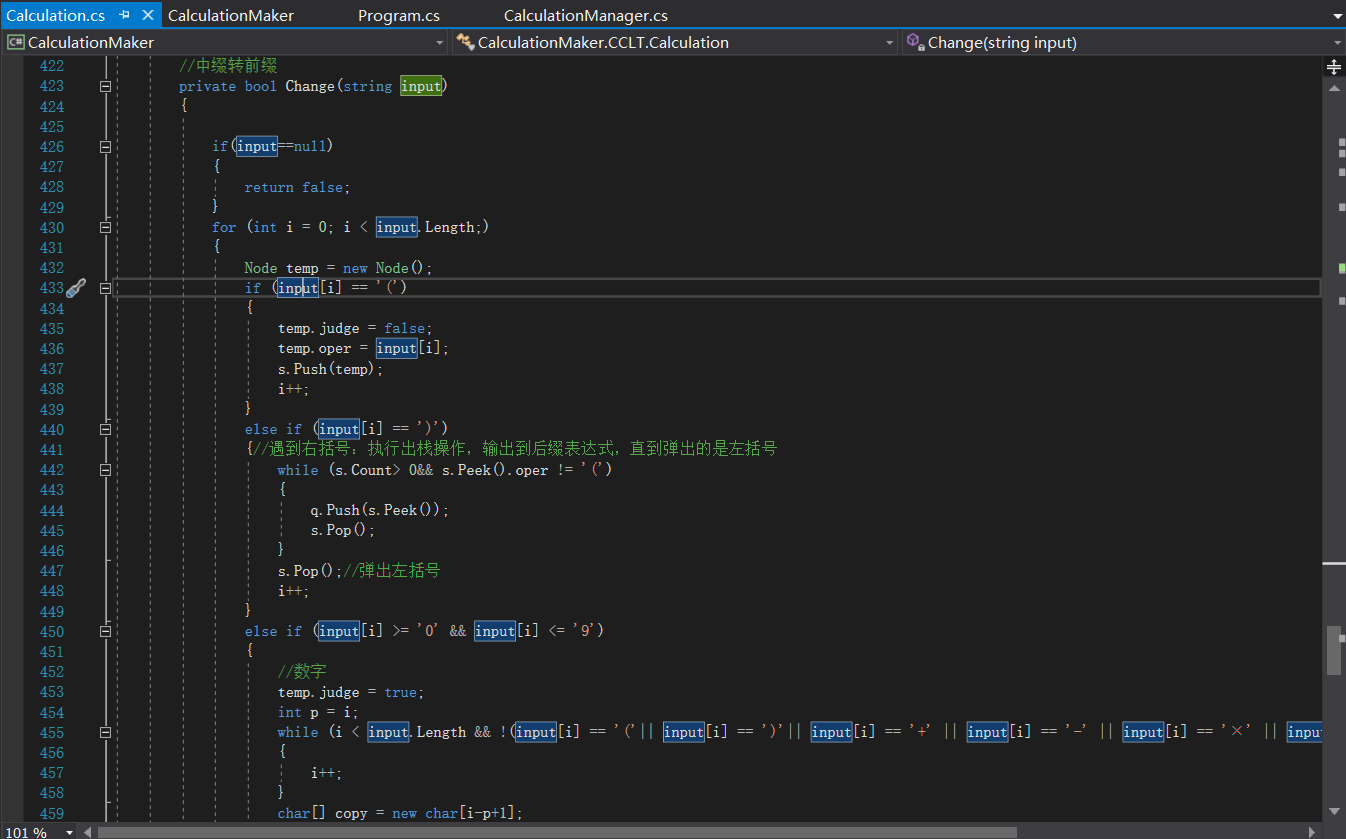
      G1aFXD.png

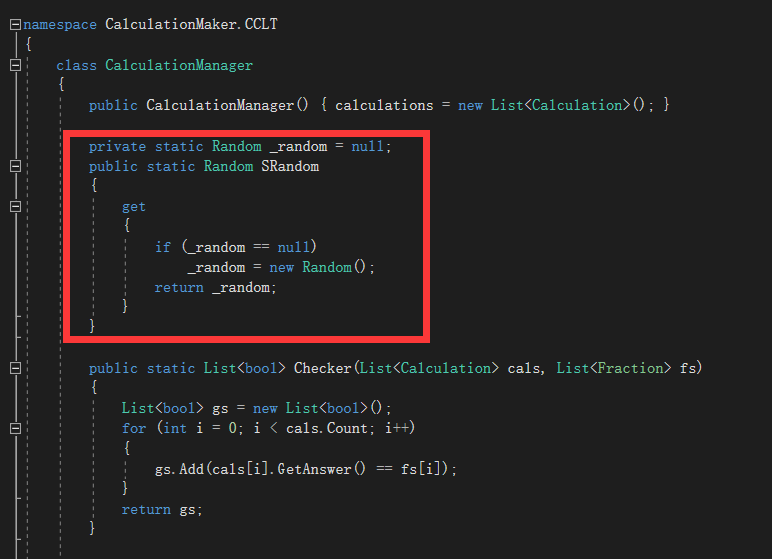
    2. 随机数生成
      创建了过多的Random对象
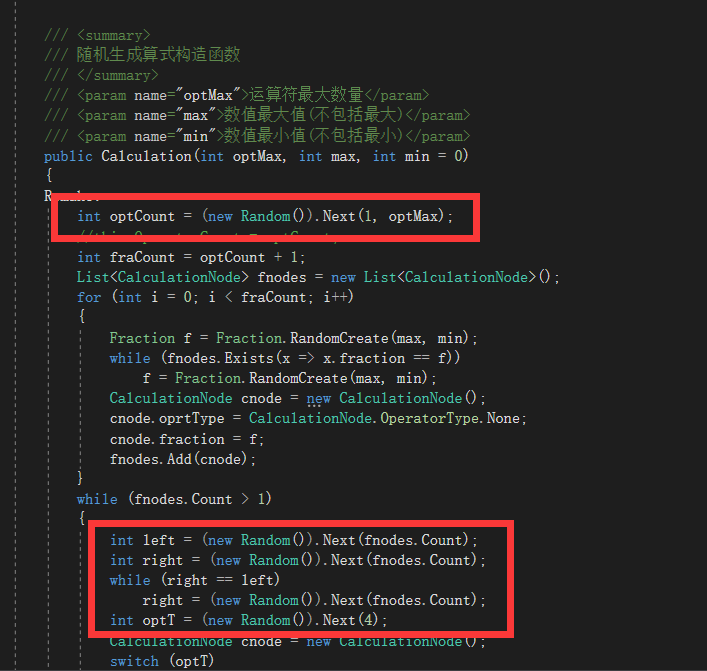
      G1aV7d.png

    解决问题

    1. 使用中间变量
      用一个char变量来装获得的字符，牺牲可以忽略不计的内存提高一大截效率
      G1amtI.png

    2. 使用静态Random对象
      使用单例类来增加随机数生成器的复用性
      单例类：
      G1a8BQ.png
      使用：
      G1a0jU.png

      G1ad3V.png

    效果拔群，从9w+ ms 缩到了 700 ms
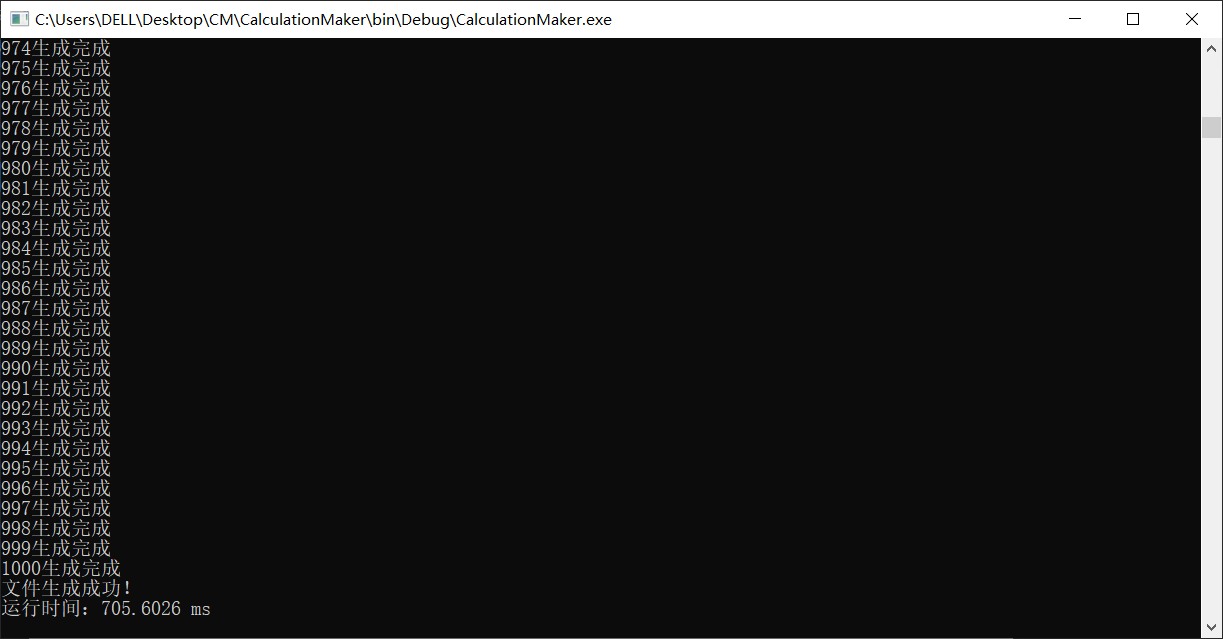
    G1ahjO.png

    来试试生成1w个
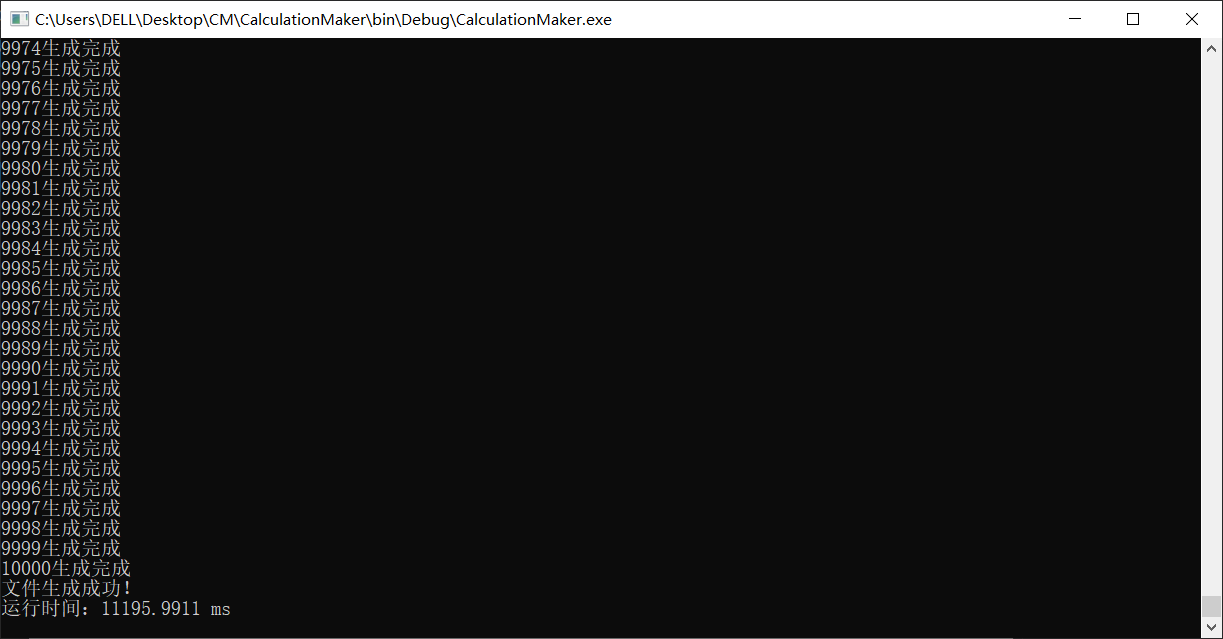
    G1afgK.png
    1.1w ms，可以接受，毕竟是1w个，估计是为了不重复，比较算式上花费时间较多

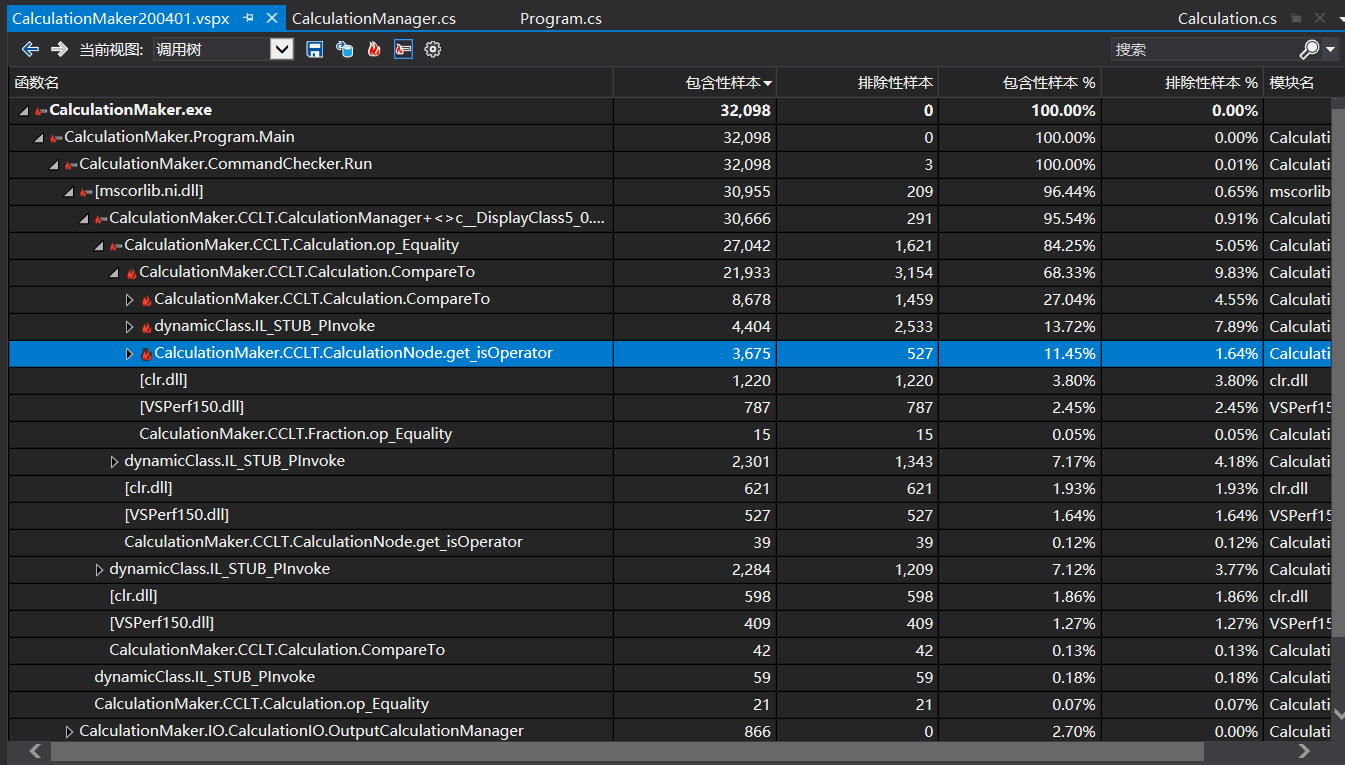
    性能探测

    对优化过的代码进行性能探测
    结果如图
    G1a5uD.png

    很显然，大部分时间都在比较算式的重复。
    比较算式是树的比较，还有考虑到加法和乘法的交换律，虽然还有优化的空间，但要回归比较的方式O(n²)的时间复杂度没跑了，提升应该不会非常大，因此更细节的优化以后有空再做。

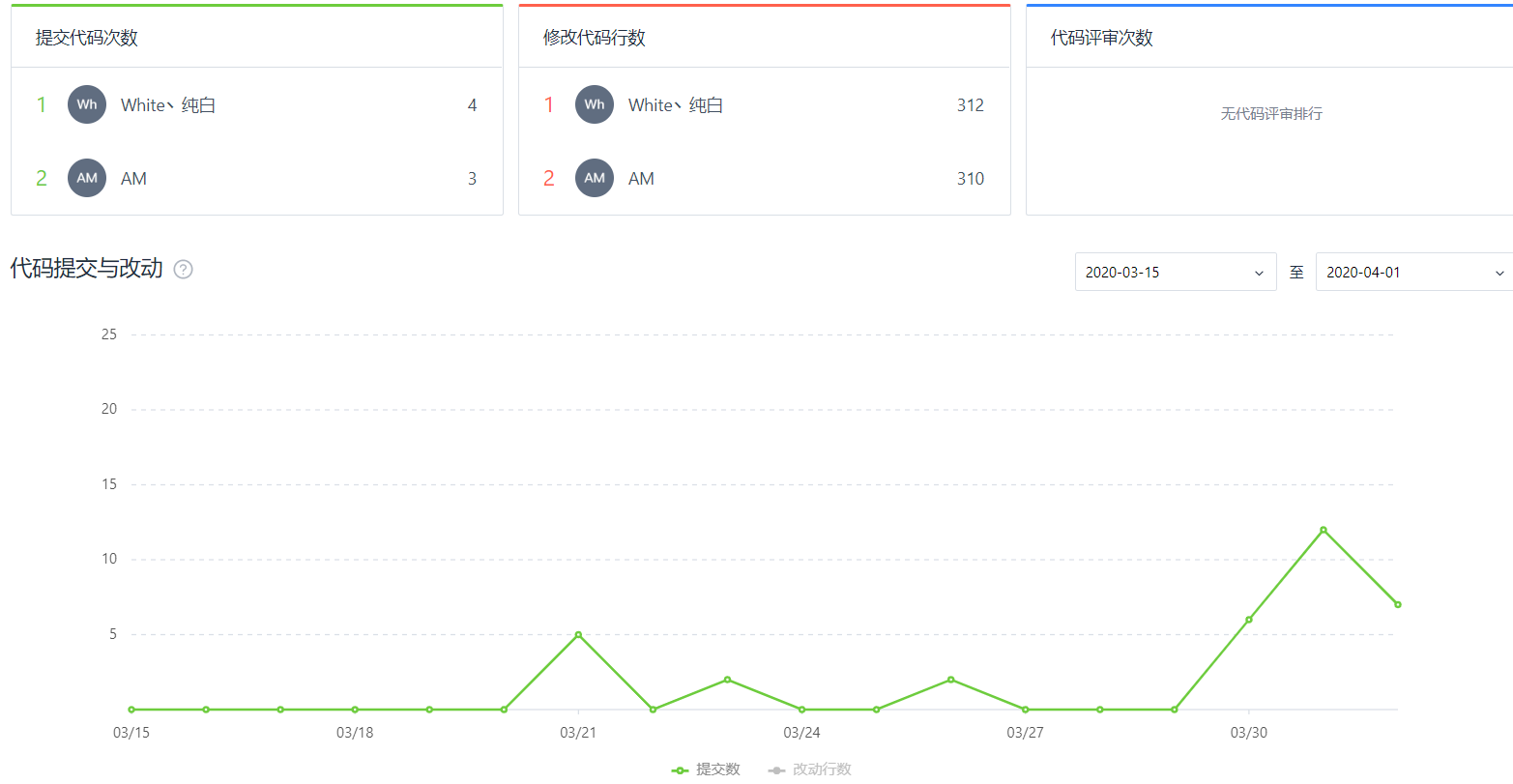
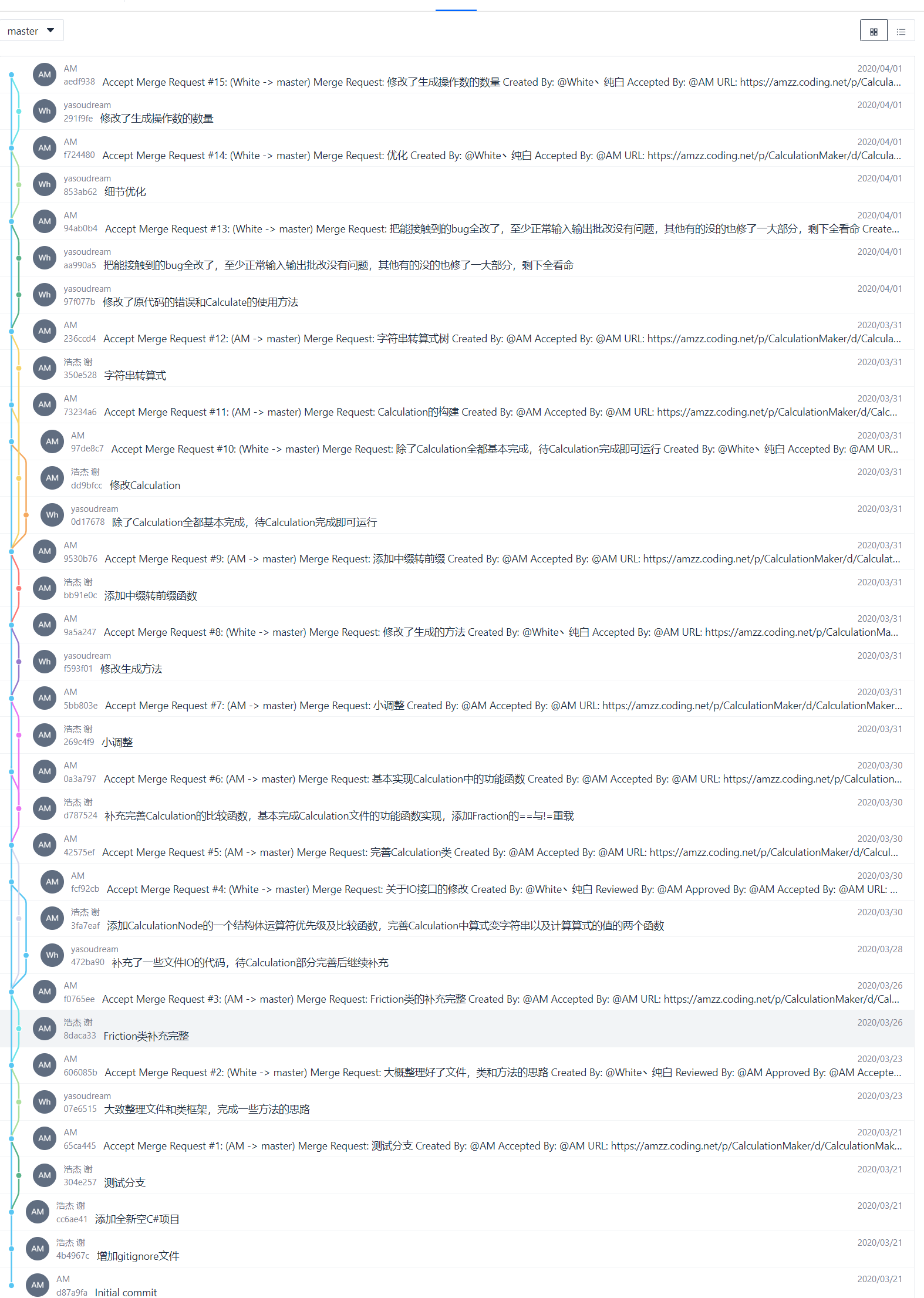
    团队协作

    ​ 项目小结：我(AM)的结对成员是软工4班张伟景(White纯白),我们使用CODING进行团队协作，将项目放于master主分支，各自创建自己的分支进行工作，提交并合并。

    ​ 我们起初看到项目要求是先一起讨论需求，以及对其进行分析，讨论功能模块化，并将功能分工进行工作，合并时写好各自模块使用文档，描述各自代码更新内容，汇报项目进度，最终有条不紊地完成了这次结对项目。

    ​ 之前我俩也进行过不少项目合作，所以配合起来比较融洽，不会出现删库跑路现象(滑稽)

    G1DpQ0.png

    G1DFwF.png

    G1DKOK.png

    *PSP2.1表格*

    *PSP2.1* *Personal Software Process Stages* *预估耗时（分钟）* *实际耗时（分钟）*
    Planning 计划 10 10
    · Estimate · 估计这个任务需要多少时间 10 10
    Development 开发 1000 900
    · Analysis · 需求分析 (包括学习新技术) 60 60
    · Design Spec · 生成设计文档 20 20
    · Design Review · 设计复审 (和同事审核设计文档) 20 20
    · Coding Standard · 代码规范 (为目前的开发制定合适的规范) 20 10
    · Design · 具体设计 100 90
    · Coding · 具体编码 400 350
    · Code Review · 代码复审 100 70
    · Test · 测试（自我测试，修改代码，提交修改） 280 280
    Reporting 报告 180 150
    · Test Report · 测试报告 50 40
    · Size Measurement · 计算工作量 60 50
    · Postmortem & Process Improvement Plan · 事后总结, 并提出过程改进计划 70 60
    合计 1200 1100
  • 相关阅读:
    Cryptography中的对称密钥加解密：fernet算法探究
    HTTPS的工作原理
    最近要写的博客
    浅谈路由器软硬件架构
    组管理、权限管理、定时任务调度、磁盘分区
    matplotlib数据可视化
    tensorflow实现简单的卷积神经网络
    tensorflow实现简单的感知机
    tensorflow实现简单的自编码器
    区域生长算法(手动选取种子点)MATLAB
  • 原文地址：https://www.cnblogs.com/AMzz/p/12611894.html
Copyright © 2011-2022 走看看