( ext{Description})
( ext{Solution})
最大流最小割定理。
首先需要明确的是求出最小割,然后将总满意值减去最小割。
首先如果没有全选的贡献就可以将 (S) 向 (x) 连一条 ( ext{Art}[x]) 的边,将 (x) 向 (T) 连一条 ( ext{Science}[x]) 的边。容易发现对于 (x) 会割掉较短边,也就弃选了这个科目(最大流被较小边的流量限制)。
如果有全选限制呢?我们看图说话(其中蓝边容量为 ( ext{infty}),( ext{B,C,D,E}) 是 ( ext A) 相邻的同学):
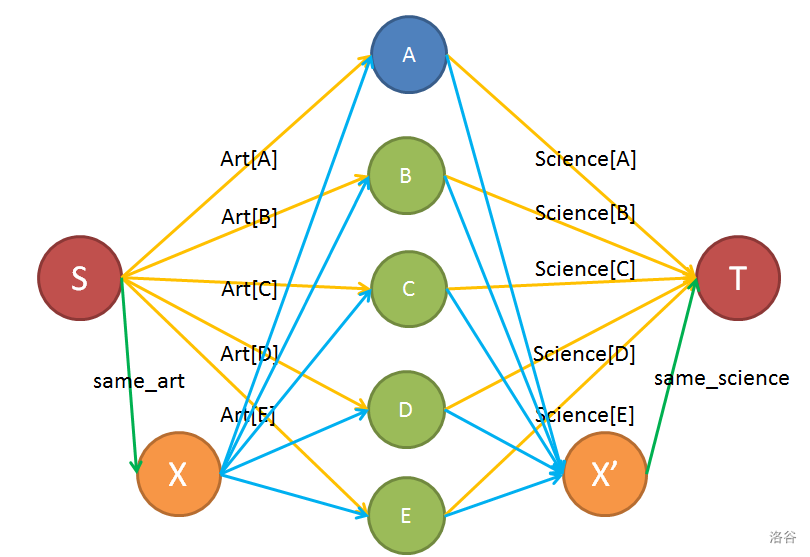
由于是最小割,蓝边一定不会被割(也可以理解为蓝边的容量不可能被耗尽)。
对于 ( ext{same_art}),可以发现如果 ( ext{Science}) 类边容量有剩余,就还有增广路,就还可以增加流量。所以如果存在 ( ext{same_art}),就一定没有 ( ext{Science}) 类边,反之亦然。
故这样建边是正确的。
( ext{Code})
#include <cstdio>
#define rep(i,_l,_r) for(register signed i=(_l),_end=(_r);i<=_end;++i)
#define fep(i,_l,_r) for(register signed i=(_l),_end=(_r);i>=_end;--i)
#define erep(i,u) for(signed i=head[u],v=to[i];i;i=nxt[i],v=to[i])
#define efep(i,u) for(signed i=Head[u],v=to[i];i;i=nxt[i],v=to[i])
#define print(x,y) write(x),putchar(y)
template <class T> inline T read(const T sample) {
T x=0; int f=1; char s;
while((s=getchar())>'9'||s<'0') if(s=='-') f=-1;
while(s>='0'&&s<='9') x=(x<<1)+(x<<3)+(s^48),s=getchar();
return x*f;
}
template <class T> inline void write(const T x) {
if(x<0) return (void) (putchar('-'),write(-x));
if(x>9) write(x/10);
putchar(x%10^48);
}
template <class T> inline T Max(const T x,const T y) {if(x>y) return x; return y;}
template <class T> inline T Min(const T x,const T y) {if(x<y) return x; return y;}
template <class T> inline T fab(const T x) {return x>0?x:-x;}
template <class T> inline T gcd(const T x,const T y) {return y?gcd(y,x%y):x;}
template <class T> inline T lcm(const T x,const T y) {return x/gcd(x,y)*y;}
template <class T> inline T Swap(T &x,T &y) {x^=y^=x^=y;}
#include <queue>
using namespace std;
const int maxn=105,inf=0x3f3f3f3f;
queue <int> q;
int dir[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
int n,m,S,T,idx,sum,dep[maxn*maxn*3],arc[maxn*maxn*3],MaxFlow;
int cnt=1,head[maxn*maxn*3],nxt[maxn*maxn*28],to[maxn*maxn*28],flow[maxn*maxn*28];
void addEdge(int u,int v,int w) {
nxt[++cnt]=head[u],to[cnt]=v,flow[cnt]=w,head[u]=cnt;
nxt[++cnt]=head[v],to[cnt]=u,flow[cnt]=0,head[v]=cnt;
}
int ID(int x,int y) {
return (x-1)*m+y;
}
bool ok(int x,int y) {
return x>=1 && x<=n && y>=1 && y<=m;
}
bool bfs() {
rep(i,0,idx) dep[i]=inf;
while(!q.empty()) q.pop();
q.push(S),arc[S]=head[S],dep[S]=0;
while(!q.empty()) {
int u=q.front(); q.pop();
erep(i,u)
if(flow[i]>0 && dep[v]==inf) {
dep[v]=dep[u]+1;
arc[v]=head[v],q.push(v);
if(v==T) return 1;
}
}
return 0;
}
int dfs(int u,int CanFlow) {
if(u==T) return CanFlow;
int SumFlow=0,d;
for(int i=arc[u];i;i=nxt[i]) {
int v=to[i];
arc[u]=i;
if(flow[i]>0 && dep[v]==dep[u]+1) {
d=dfs(v,Min(CanFlow,flow[i]));
if(!d) dep[v]=inf;
SumFlow+=d,CanFlow-=d;
flow[i]-=d,flow[i^1]+=d;
if(!CanFlow) break;
}
}
return SumFlow;
}
void Dinic() {
while(bfs()) MaxFlow+=dfs(S,inf);
}
int main() {
int x;
n=read(9),m=read(9); S=0,T=idx=n*m+1;
rep(i,1,n) rep(j,1,m) x=read(9),addEdge(S,ID(i,j),x),sum+=x;
rep(i,1,n) rep(j,1,m) x=read(9),addEdge(ID(i,j),T,x),sum+=x;
rep(i,1,n) rep(j,1,m) {
x=read(9),sum+=x; ++idx;
addEdge(S,idx,x),addEdge(idx,ID(i,j),inf);
rep(d,0,3) if(ok(i+dir[d][0],j+dir[d][1])) addEdge(idx,ID(i+dir[d][0],j+dir[d][1]),inf);
}
rep(i,1,n) rep(j,1,m) {
x=read(9),sum+=x; ++idx;
addEdge(idx,T,x),addEdge(ID(i,j),idx,inf);
rep(d,0,3) if(ok(i+dir[d][0],j+dir[d][1])) addEdge(ID(i+dir[d][0],j+dir[d][1]),idx,inf);
}
Dinic();
print(sum-MaxFlow,'
');
return 0;
}
( ext{Reference})
(mathtt{jun})头吉吉 的配图。