Snacks
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 3213 Accepted Submission(s): 743
Problem Description
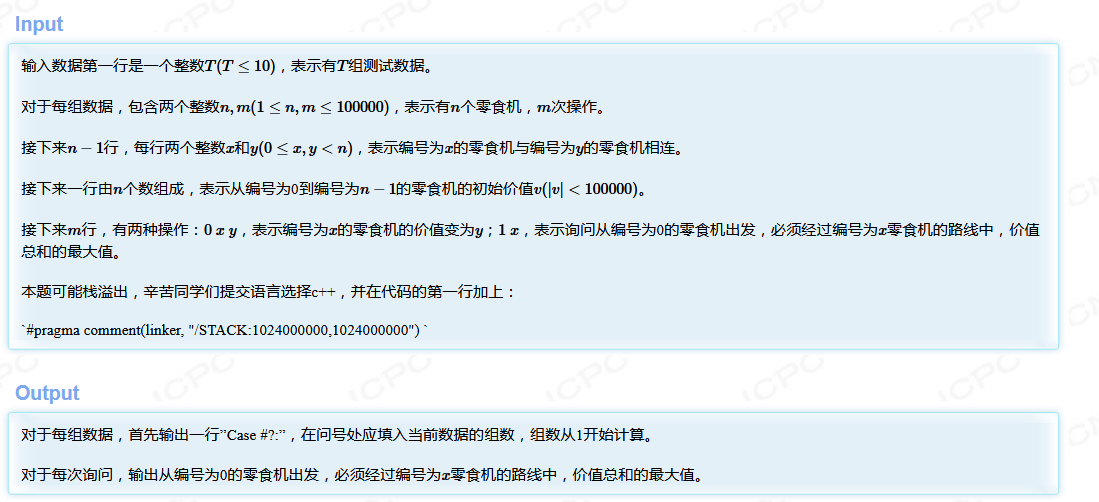
百度科技园内有n个零食机,零食机之间通过n−1条路相互连通。每个零食机都有一个值v,表示为小度熊提供零食的价值。
由于零食被频繁的消耗和补充,零食机的价值v会时常发生变化。小度熊只能从编号为0的零食机出发,并且每个零食机至多经过一次。另外,小度熊会对某个零食机的零食有所偏爱,要求路线上必须有那个零食机。
为小度熊规划一个路线,使得路线上的价值总和最大。
由于零食被频繁的消耗和补充,零食机的价值v会时常发生变化。小度熊只能从编号为0的零食机出发,并且每个零食机至多经过一次。另外,小度熊会对某个零食机的零食有所偏爱,要求路线上必须有那个零食机。
为小度熊规划一个路线,使得路线上的价值总和最大。
Sample Input
1
6 5
0 1
1 2
0 3
3 4
5 3
7 -5 100 20 -5 -7
1 1
1 3
0 2 -1
1 1
1 5
Sample Output
Case #1:
102
27
2
20
Source
中文题 题意不解释
修改每个节点的权值 改变的是这个点的子树中的点到根节点的价值和
求根节点路过这个点的路径的最大和 就是求根节点到这个点已经这个点的子树中的那个最大价值和
我们就可以用DFS序 得到每个点的时间戳 将这个时间戳转化为线段树 修改一个点的权值 就相当他区间修改 修改这个区间的权值
查询也就是查询区间的最大值
1 #pragma comment(linker, "/STACK:1024000000,1024000000") 2 #include<iostream> 3 #include<cstdio> 4 #include<algorithm> 5 #include<cstring> 6 #include<cstdlib> 7 #include<string.h> 8 #include<set> 9 #include<vector> 10 #include<queue> 11 #include<stack> 12 #include<map> 13 #include<cmath> 14 typedef long long ll; 15 typedef unsigned long long LL; 16 using namespace std; 17 const double PI=acos(-1.0); 18 const double eps=0.0000000001; 19 const int INF=1e9; 20 const int N=500000+100; 21 int head[N]; 22 int tot; 23 ll a[N]; 24 ll b[N]; 25 int n,m; 26 struct NOde{ 27 int l,r; 28 ll val; 29 ll lazy; 30 }tree[N*4]; 31 struct node{ 32 int to,next; 33 }edge[N<<1]; 34 int L[N],R[N]; 35 int time; 36 ll dis[N]; 37 void init(){ 38 memset(head,-1,sizeof(head)); 39 tot=0; 40 time=0; 41 } 42 void add(int u,int v){ 43 edge[tot].to=v; 44 edge[tot].next=head[u]; 45 head[u]=tot++; 46 } 47 void DFS(int x,int fa){ 48 L[x]=++time; 49 b[time]=x; 50 for(int i=head[x];i!=-1;i=edge[i].next){ 51 int v=edge[i].to; 52 if(v==fa)continue; 53 a[v]=a[x]+a[v]; 54 DFS(v,x); 55 } 56 R[x]=time; 57 } 58 void pushdown(int pos){ 59 if(tree[pos].lazy){ 60 tree[pos<<1].val+=tree[pos].lazy; 61 tree[pos<<1|1].val+=tree[pos].lazy; 62 tree[pos<<1].lazy+=tree[pos].lazy; 63 tree[pos<<1|1].lazy+=tree[pos].lazy; 64 tree[pos].lazy=0; 65 66 } 67 } 68 void build(int left,int right,int pos){ 69 // cout<<55<<endl; 70 tree[pos].l=left; 71 tree[pos].r=right; 72 tree[pos].lazy=0; 73 int mid=tree[pos].l+tree[pos].r>>1; 74 if(tree[pos].l==tree[pos].r){ 75 tree[pos].val=a[b[left]]; 76 return ; 77 } 78 build(left,mid,pos<<1); 79 build(mid+1,right,pos<<1|1); 80 tree[pos].val=max(tree[pos<<1].val,tree[pos<<1|1].val); 81 82 } 83 void update(int left,int right,int pos,ll x){ 84 if(tree[pos].l==left&&tree[pos].r==right){ 85 tree[pos].lazy+=x; 86 tree[pos].val+=x; 87 return ; 88 } 89 pushdown(pos); 90 int mid=(tree[pos].l+tree[pos].r)>>1; 91 if(mid>=right)update(left,right,pos<<1,x); 92 else if(mid<left)update(left,right,pos<<1|1,x); 93 else{ 94 update(left,mid,pos<<1,x); 95 update(mid+1,right,pos<<1|1,x); 96 } 97 tree[pos].val=max(tree[pos<<1].val,tree[pos<<1|1].val); 98 } 99 ll query(int left,int right,int pos){ 100 if(tree[pos].l==left&&tree[pos].r==right){ 101 return tree[pos].val; 102 } 103 pushdown(pos); 104 int mid=(tree[pos].l+tree[pos].r)>>1; 105 if(mid>=right){ 106 return query(left,right,pos<<1); 107 } 108 else if(left>mid){ 109 return query(left,right,pos<<1|1); 110 } 111 else{ 112 return max(query(left,mid,pos<<1),query(mid+1,right,pos<<1|1)); 113 } 114 } 115 int main(){ 116 int t; 117 scanf("%d",&t); 118 int Case=1; 119 while(t--){ 120 init(); 121 scanf("%d%d",&n,&m); 122 int u,v; 123 for(int i=1;i<n;i++){ 124 scanf("%d%d",&u,&v); 125 add(u,v); 126 add(v,u); 127 } 128 for(int i=0;i<n;i++){ 129 scanf("%I64d",&a[i]); 130 dis[i]=a[i]; 131 } 132 DFS(0,-1); 133 build(1,time,1); 134 int flag; 135 int x; 136 ll y; 137 printf("Case #%d: ",Case++); 138 while(m--){ 139 scanf("%d",&flag); 140 if(flag==0){ 141 scanf("%d%I64d",&x,&y); 142 update(L[x],R[x],1,(ll)y-dis[x]); 143 dis[x]=y; 144 } 145 else{ 146 scanf("%d",&x); 147 ll ans=query(L[x],R[x],1); 148 printf("%I64d ",ans); 149 } 150 151 } 152 153 } 154 }