回归

回归

　　回归的英文Regression，单词regress本意是退化，回退

　　回归的意思是倒推，由果索因，分为线性和非线性

　　由大量的函数结果和自变量反推回函数表达式的过程

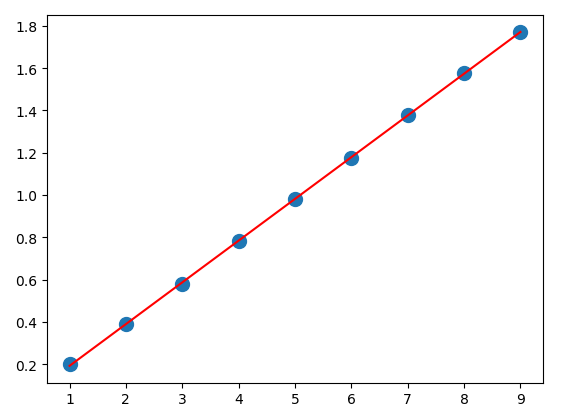
　　用python实现线性回归的例子

import numpy as np
import matplotlib.pyplot as plt
#原始数据
x=[1,2,3,4,5,6,7,8,9]
y=[0.199,0.389,0.580,0.783,0.980,1.177,1.380,1.575,1.771]
#生成1矩阵并追加在x矩阵之后
A=np.vstack([x,np.ones(len(x))]).T
#调用最小二乘法
a,b=np.linalg.lstsq(A,y)[0]
#转化为numpy array
x=np.array(x)
y=np.array(y)
#画图
plt.plot(x,y,'o',label='Original data',markersize=10)
plt.plot(x,a*x+b,'r',label='Fitted line')
plt.show()

 

过拟合：我们通过对数据样本的归纳和抽象，最后得到一个完整的数据映射模型（拟合），但在归纳的过程中，可能会出现迎合所有样本点甚至是噪声点而使得模型过于复杂，失去泛化能力的情况

　　泛化能力：通过学习得到的模型对未知数据的预测能力

　　解决过拟合的办法：1）增加训练样本，2）在建模的过程中舍弃典型的噪声数据

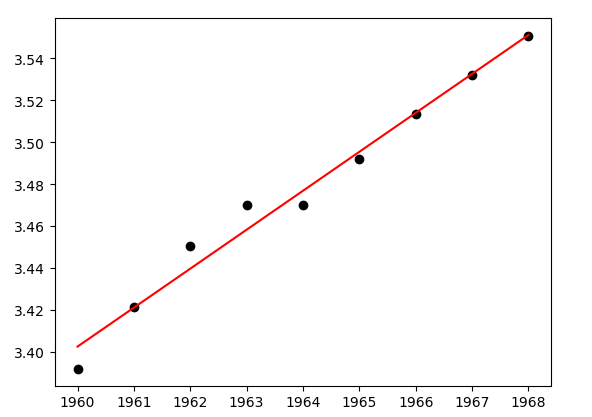
　　欠拟合：与过度拟合相反，由于建模不当导致误差太大

import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
#原始数据
T=[1960,1961,1962,1963,1964,1965,1966,1967,1968]
S=[29.72,30.61,31.51,32.13,32.14,32.85,33.56,34.20,34.83]

xdata=np.array(T)
ydata=np.log(np.array(S))

def func(x,a,b):
    return a+b*xdata

#使用非线性最小二乘法拟合函数
popt,pcov=curve_fit(func,xdata,ydata)

#画图
plt.plot(xdata,ydata,'ko',label="Original Noised Data")
plt.plot(xdata,func(xdata,*popt),'r',label="Fitted Curve")
plt.show()