PAT Advanced Level 1099

099 Build A Binary Search Tree（30 分）

A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
• Both the left and right subtrees must also be binary search trees.

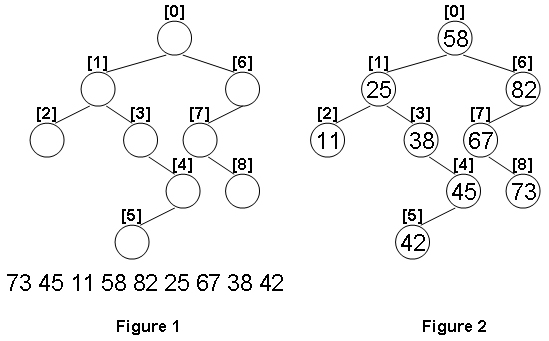
Given the structure of a binary tree and a sequence of distinct integer keys, there is only one way to fill these keys into the tree so that the resulting tree satisfies the definition of a BST. You are supposed to output the level order traversal sequence of that tree. The sample is illustrated by Figure 1 and 2.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤100) which is the total number of nodes in the tree. The next N lines each contains the left and the right children of a node in the format left_index right_index, provided that the nodes are numbered from 0 to N−1, and 0 is always the root. If one child is missing, then −1 will represent the NULL child pointer. Finally N distinct integer keys are given in the last line.

Output Specification:

For each test case, print in one line the level order traversal sequence of that tree. All the numbers must be separated by a space, with no extra space at the end of the line.

Sample Input:

9
1 6
2 3
-1 -1
-1 4
5 -1
-1 -1
7 -1
-1 8
-1 -1
73 45 11 58 82 25 67 38 42

Sample Output:

58 25 82 11 38 67 45 73 42

/**********************
author: yomi
date: 18.8.21
ps: AC率0.67的题 果然我也一次过
**********************/
#include <iostream>
#include <queue>
#include <algorithm>
using namespace std;
int n;
struct Node
{
    int data;
    int l, r;
}node[110];
bool vis[110];
queue<int>q;
int level[110], cnt, in[110], cnt1;
void bfs()
{
    while(!q.empty())
        q.pop();
    q.push(0);
    vis[0] = true;
    while(!q.empty()){
        int a = q.front();
        level[cnt++] = node[a].data;
        q.pop();
        if(node[a].l!=-1){
            q.push(node[a].l);
        }
        if(node[a].r!=-1){
            q.push(node[a].r);
        }
    }

}
void in_order(int index)
{
    if(node[index].l!=-1)
        in_order(node[index].l);
    node[index].data = in[cnt1++];
    if(node[index].r!=-1)
        in_order(node[index].r);
}
int main()
{

    cin >> n;
    for(int i=0; i<n; i++){
        cin >> node[i].l >> node[i].r;
    }
    for(int i=0; i<n; i++){
        cin >> in[i];
    }
    sort(in, in+n);
    in_order(0);
    bfs();
    for(int i=0; i<cnt-1; i++){
        cout << level[i] << ' ';
    }
    cout << level[cnt-1];
    return 0;
}
/**
9
1 6
2 3
-1 -1
-1 4
5 -1
-1 -1
7 -1
-1 8
-1 -1
73 45 11 58 82 25 67 38 42
**/