本文转载自王陸的文字,转载仅作学习使用。
定义概览
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
问题描述:在无向图 G=(V,E) 中,假设每条边 E[i] 的长度为 w[i],找到由顶点 V0 到其余各点的最短路径。(单源最短路径)
算法描述
算法思想:
设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
算法步骤:
a.初始时,S只包含源点,即S={v},v的距离为0。U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则<u,v>正常有权值,若u不是v的出边邻接点,则<u,v>权值为∞。
b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。
执行动画过程如下图

动图太快可以看下面的例子:
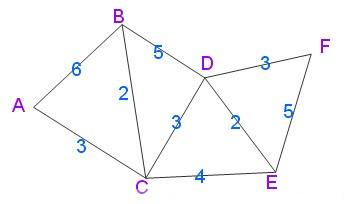

重点需要理解这句拗口的”按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度”
实际上,Dijkstra 算法是一个排序过程,就上面的例子来说,是根据A到图中其余点的最短路径长度进行排序,路径越短越先被找到,路径越长越靠后才能被找到,要找A到F的最短路径,我们依次找到了
A –> C 的最短路径 3
A –> C –> B 的最短路径 5
A –> C –> D 的最短路径 6
A –> C –> E 的最短路径 7
A –> C –> D –> F 的最短路径 9
**为什么Dijkstra 算法不适用于带负权的图? **
就上个例子来说,当把一个点选入集合S时,就意味着已经找到了从A到这个点的最短路径,比如第二步,把C点选入集合S,这时已经找到A到C的最短路径了,但是如果图中存在负权边,就不能再这样说了。举个例子,假设有一个点Z,Z只与A和C有连接,从A到Z的权为50,从Z到C的权为-49,现在A到C的最短路径显然是A –> Z –> C
再举个例子:
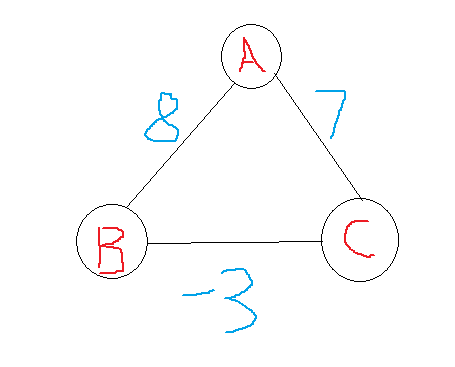
在这个图中,求从A到C的最短路,如果用Dijkstra根据贪心的思想,选择与A最接近的点C,长度为7,以后不再变化。但是很明显此图最短路为5。归结原因是Dijkstra采用贪心思想,不从整体考虑结果,只从当前情况考虑选择最优。
代码模板
#include<stdio.h>
#include<string.h>
#define inf 0x3f3f3f3f
int map[110][110],dis[110],visit[110];
/*
关于三个数组:map数组存的为点边的信息,比如map[1][2]=3,表示1号点和2号点的距离为3
dis数组存的为起始点与每个点的最短距离,比如dis[3]=5,表示起始点与3号点最短距离为5
visit数组存的为0或者1,1表示已经走过这个点。
*/
int n,m;
int dijstra()
{
int i,j,pos=1,min,sum=0;
memset(visit,0,sizeof(visit));//初始化为.,表示开始都没走过
for(i=1; i<=n; ++i)
{
dis[i]=map[1][i];
}
visit[1]=1;
dis[1]=0;
for(i=1; i<n; i++)
{
min=inf;
for(j=1; j<=n; ++j)
{
if(visit[j]==0&&min>dis[j])
{
min=dis[j];
pos=j;
}
}
visit[pos]=1;//表示这个点已经走过
for(j=1; j<=n; ++j)
{
if(visit[j]==0&&dis[j]>dis[pos]+map[pos][j])//更新dis的值
dis[j]=dis[pos]+map[pos][j];
}
}
return dis[n];
}
int main()
{
int i,j;
while(~scanf("%d%d",&n,&m),n||m)//n表示n个点,m表示m条边
{
for(i=1; i<=n; ++i)
{
for(j=1; j<=n; ++j)
{
map[i][j]=inf;//开始时将每条边赋为最大值
}
}
int a,b,c;
for(i=1; i<=m; ++i)
{
scanf("%d%d%d",&a,&b,&c);
if(c<map[a][b])//防止有重边
map[a][b]=map[b][a]=c;
}
int count=dijstra();
printf("%d
",count);
}
return 0;
}
邻接表实现:
#include<stdio.h>
#include<string.h>
#include<vector>
#include<algorithm>
#define INF 0x3f3f3f3f
using namespace std;
struct node
{
int end;///终点
int power;///权值
} t;
int n;///n为点数
vector<node>q[500001];///邻接表储存图的信息
int dis[500001];///距离
int vis[500001];///标记数组
void Dijkstra(int start,int end)
{
int i,len,j,pos;
memset(vis,0,sizeof(vis));
for(i=0; i<=n; i++)
{
dis[i]=INF;
}
len=q[start].size();
for(i=0; i<len; i++)
{
if(q[start][i].power<dis[q[start][i].end])
{
dis[q[start][i].end]=q[start][i].power;
}
}///从起点开始的dis数组更新
vis[start]=1;
for(j=0; j<n-1; j++)
{
int pos,min=INF;
for(i=1; i<=n; i++)
{
if(vis[i]!=0&&dis[i]<min)
{
min=dis[i];
pos=i;///找到未访问节点中权值最小的
}
}
vis[pos]=1;
len=q[pos].size();///再次更新dis数组
for(j=0; j<len; j++)
{
if(vis[q[pos][j].end]==0&&dis[q[pos][j].end]>q[pos][j].power+dis[pos])
{
dis[q[pos][j].end] = q[pos][j].power+dis[pos];
}
}
}
printf("%d
",dis[end]);
}
int main()
{
int m,i;
int begin,end,power;
int a,b;
while(scanf("%d%d",&n,&m)!=EOF)
{
for(i=0; i<=n; i++)
{
q[i].clear();///将victor数组清空
}
for(i=0; i<m; i++)
{
scanf("%d%d%d",&begin,&end,&power);///输入
t.end=end;
t.power=power;
q[begin].push_back(t);
t.end=begin;///无向图
t.power=power;
q[end].push_back(t);
}
scanf("%d%d",&a,&b);///输入起点与终点
Dijkstra(a,b);
}
return 0;
}