计蒜客-----结果填空：方阵

这个题目听完讲解感觉也就那么回事。

假设有两个点(x1，y1)和（x2，y2），a=x1-x2，b=y1-y2，那么如果说__gcd(a,b)==1,那么他们一定可以看到，具体为什么，我们可以根据三角形来解释

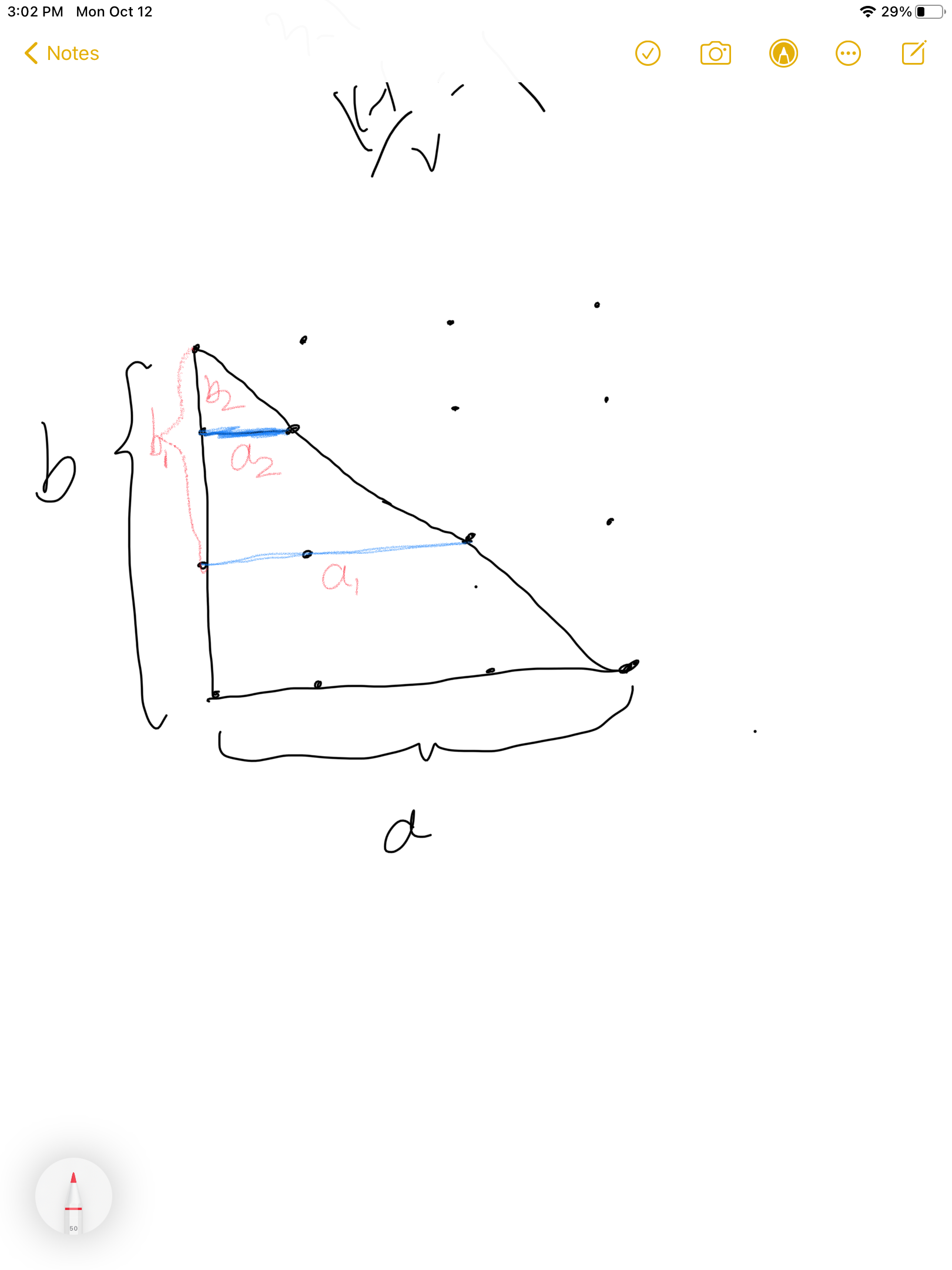
如果说a和b存在gcd，那么一定会存在a1和b1，a2，b2...，这也就是为什么a和b的gcd应该等于1。

另外如果两个学生可以看见，我们只关注这两个学生的相对距离就可以了，与这个学生具体在哪个位置没有关系。

所以我们可以枚举横向的差值和纵向的差值，如果gcd==1并且满足距离要求，那么他对答案的贡献就应该是(n-      i)*(n-j)（i表示横向差值，j表示纵向差值）
为什么是这样呢？

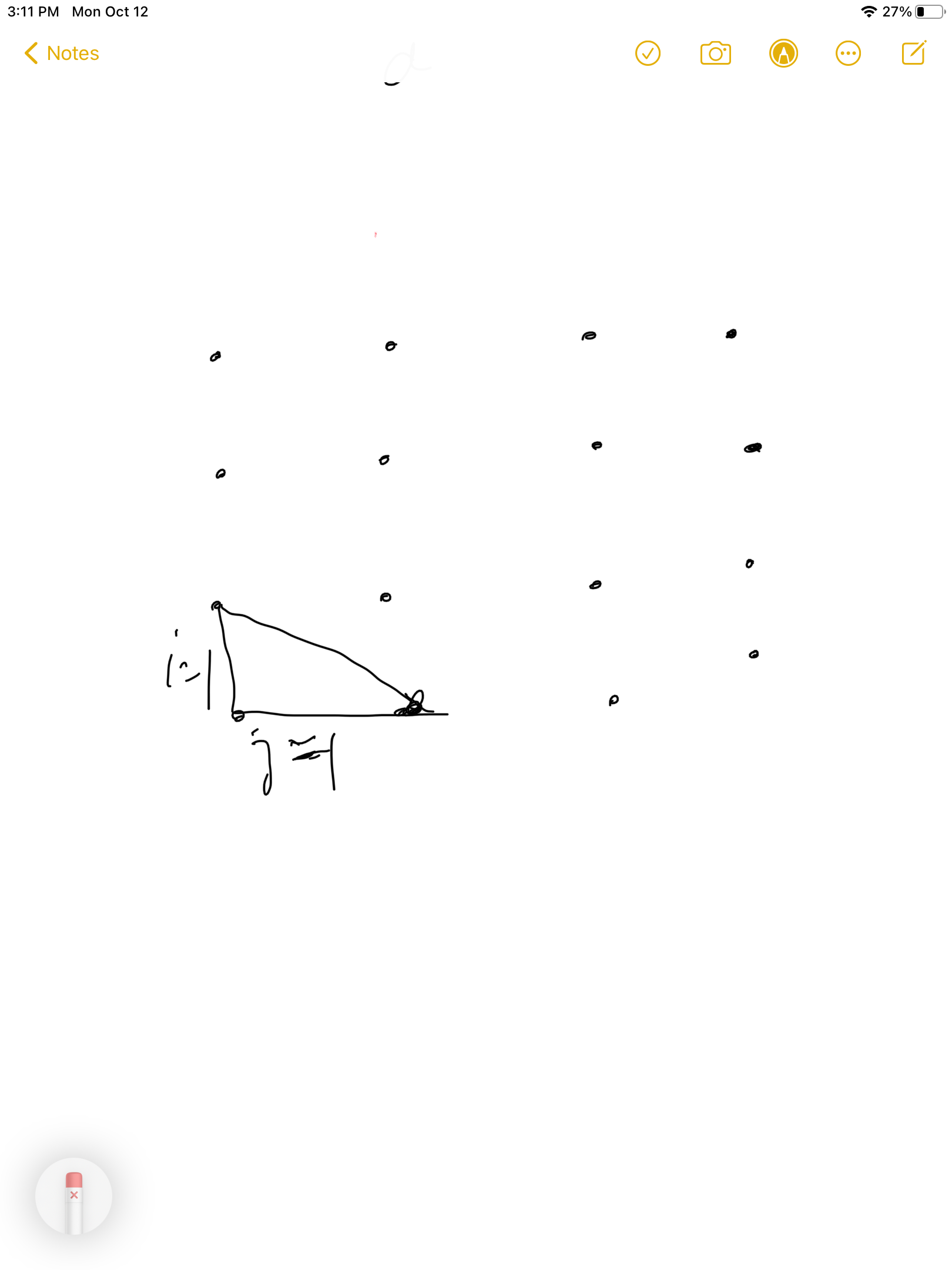
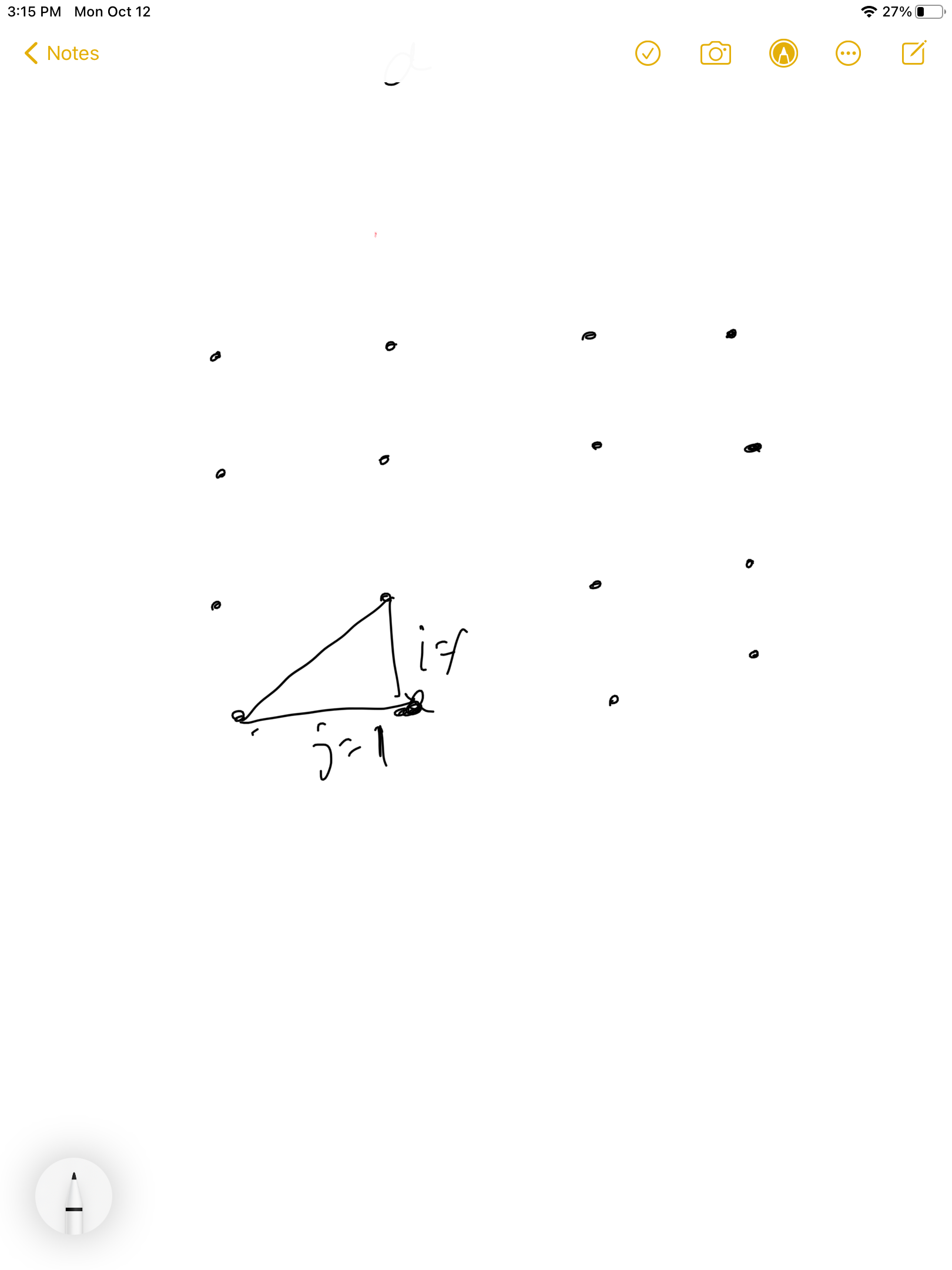
左下角的三角形可以向右移动两个，加上他自己就是3个，同理向上也是3个，因此对答案的贡献就是3*3=9个。

最后我们还需要*2，这样又是另外一种情况

code:

#include<bits/stdc++.h>
using namespace std;
const long long  MOD=1e9+7;
int main() {
    long long  n=1000;
    long long  k=500;
    long long  ans=n*(n-1);
    for(long long  i=1;i<n;i++){
        for(long long  j=1;j<n;j++){
            if(__gcd(i,j)!=1) continue ;
            if(i*i+j*j>k*k) continue ;
            ans=ans+(n-i)*(n-j)%MOD;
            ans=ans%MOD;
        }
    }
    ans=ans*2%MOD;
    cout<<ans<<endl;
    return 0;
}