网络流

先上板

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#include<vector>
const int maxn=2050;
const int INF=1e9;
using namespace std;
int ans,n,m,xx,yy,cur[maxn],ad[maxn],s=0,t=201,dis[maxn];
struct edge{
    int from,to,flow,cup;
    edge(int from,int to,int flow,int cup):from(from),to(to),flow(flow),cup(cup){}
};
vector<edge>edges;
vector<int>g[maxn];
void add(int u,int v,int w){
   edges.push_back(edge(u,v,0,w));
   edges.push_back(edge(v,u,0,0));
   int t=edges.size();
   g[u].push_back(t-2);
   g[v].push_back(t-1);
} 
queue<int>que;
int bfs(int s,int t){
  memset(dis,0,sizeof(dis));
  dis[s]=1;
  que.push(s);
  while(!que.empty() ){
    int x=que.front();que.pop() ;
    for(int i=0;i<g[x].size();i++){
      edge t=edges[g[x][i]];
      if(!dis[t.to]&&t.cup>t.flow){
        dis[t.to]=dis[x]+1;
        que.push(t.to);
      }
    }
  }
  return dis[t];
}
int dfs(int x,int a){
    if(x==t||a==0) return a;
    int fl=0,c;
    for(int &i=cur[x];i<g[x].size();i++){
       edge &t=edges[g[x][i]];
       if(dis[t.to]==dis[x]+1&&(c=dfs(t.to,min(a,t.cup-t.flow)))){
            t.flow+=c;
            edges[g[x][i]^1].flow-=c;
         fl+=c;
            a-=c;
       } 
       if(a==0) break;
    }
    return fl;
}
void Dinic(int s,int t){
    while(bfs(s,t)){
     memset(cur,0,sizeof(cur));
     ans+=dfs(s,INF);
    }
}
int main()
{
   scanf("%d%d",&m,&n);
   for(;;){
     scanf("%d%d",&xx,&yy);
     if(xx==-1&&yy==-1) break;
     yy+=100;
     if(!ad[xx]) add(s,xx,1),ad[xx]=1;
     add(xx,yy,1);
     if(!ad[yy]) add(yy,t,1),ad[yy]=2;
   }
   Dinic(s,t);
     printf("%d
",ans);
     for(int i=0;i<edges.size();i++){
     edge x=edges[i];
     if(x.from !=s&&x.to !=t&&x.cup&&x.flow==x.cup){
         printf("%d %d
",x.from,x.to-100);
     }
   }
   return 0;
}

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#include<vector>
const int maxn=100000+10; 
using namespace std;
int ans,flow,from,to,cup,n,m,s,t,a[maxn],p[maxn];
struct Edge{
    int from,to,cup,flow;
    Edge(int from,int to,int cup,int flow):from(from),to(to),cup(cup),flow(flow){}
};
vector<Edge>edges;
vector<int> G[maxn];
void add(int from,int to,int cup){
    edges.push_back(Edge(from,to,cup,0));
    edges.push_back(Edge(to,from,0,0));
    int m=edges.size() ;
    G[from].push_back(m-2);
    G[from].push_back(m-1); 
}
queue<int>que;
int bfs(int s,int t){
    //memset(p,-1,sizeof(p));
    memset(a,0,sizeof(a));
    while(!que.empty()) que.pop();
    que.push(s);
    a[s]=1e9;
    while(!que.empty() ){
        int x=que.front();que.pop();
        for(int i=0;i<G[x].size() ;i++){
            Edge tep=edges[G[x][i]];
            if(!a[tep.to ]&&tep.cup >tep.flow ){
            a[tep.to ]=min(a[x],tep.cup -tep.flow );
            p[tep.to ]=G[x][i];
                que.push(tep.to );
            }
        }
        if(a[t]) return 1;
    } 
    return 0;
}
int EK(int s,int t){
    ans=0;
    while(bfs(s,t)){
        for(int i=t;i!=s;i=edges[p[i]].from){
            edges[p[i]].flow+=a[t];
            edges[p[i]^1].flow-=a[t];
        }
        ans+=a[t];
    }
    return ans;
}
int main()
{
  scanf("%d%d%d%d",&n,&m,&s,&t);
  for(int i=1;i<=m;i++){
      scanf("%d%d%d",&from,&to,&cup);
      add(from,to,cup);
  } 
  printf("%d
",EK(s,t));
   return 0;
}

//Twenty
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#include<vector>
const int maxn=5005;
const int maxm=50005;
int a[maxn],vis[maxn],dis[maxn],ansf,ansv,u,v,c,w,n,m,s,t,pre[maxm];
using namespace std;
struct edge{
    int from,to,cup,flow,val;
    edge(int from,int to,int cup,int flow,int val):from(from),to(to),cup(cup),flow(flow),val(val){}
};
vector<int>g[maxn];
vector<edge>edges;
void add(int from,int to,int cup,int val){
    edges.push_back(edge(from,to,cup,0,val));
    edges.push_back(edge(to,from,0,0,-val));
    int x=edges.size();
    g[from].push_back(x-2);
    g[to].push_back(x-1); 
}
queue<int>que;
int spfa(int s,int t){
    memset(vis,0,sizeof(vis));
    memset(dis,127,sizeof(dis));
    memset(a,0,sizeof(a));
    que.push(s); vis[s]=1;dis[s]=0;a[s]=1e9;
    while(!que.empty() ){
        int x=que.front() ;que.pop() ;
        vis[x]=0;
        for(int i=0;i<g[x].size();i++){
            edge now=edges[g[x][i]];
            if(now.flow<now.cup&&dis[now.to ]>dis[now.from ]+now.val ){
                dis[now.to ]=dis[now.from ]+now.val ;
                a[now.to]=min(a[now.from],now.cup-now.flow); 
                pre[now.to]=g[x][i];
                if(!vis[now.to ]){
                    vis[now.to]=1;
                    que.push(now.to); 
                }
            }
        }
    }
    return a[t];     
}
void EK(int s,int t)
{
    while(spfa(s,t)){
        for(int i=t;i!=s;i=edges[pre[i]].from){
           edges[pre[i]].flow+=a[t];
           ansv+=a[t]*edges[pre[i]].val;
           edges[pre[i]^1].flow-=a[t];
        }
        ansf+=a[t];
    }
}
int main()
{
   scanf("%d%d%d%d",&n,&m,&s,&t);
   for(int i=1;i<=m;i++){
       scanf("%d%d%d%d",&u,&v,&c,&w);
       add(u,v,c,w);}
       EK(s,t);
       printf("%d %d",ansf,ansv);
   return 0;
}

//Twenty
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#include<vector>
const int maxn=299*299; 
const int INF=0x7fffffff;
int n,m,dis[maxn],s,t,cur[maxn],ans,du[maxn],x,y,d,u,dow[maxn];
using namespace std;
struct edge{
    int from,to,flow,cup;
    edge(int from,int to,int flow,int cup):from(from),to(to),flow(flow),cup(cup){}
};
vector<int>tmp;
vector<edge>edges;
vector<int>g[maxn];
void add(int u,int v,int w){
   edges.push_back(edge(u,v,0,w));
   edges.push_back(edge(v,u,0,0));
   int t=edges.size();
   g[u].push_back(t-2);
   g[v].push_back(t-1);
} 
queue<int>que;
int bfs(int s,int t){
  memset(dis,0,sizeof(dis));
  dis[s]=1;
  que.push(s);
  while(!que.empty() ){
    int x=que.front();que.pop() ;
    for(int i=0;i<g[x].size();i++){
      edge t=edges[g[x][i]];
      if(!dis[t.to]&&t.cup>t.flow){
        dis[t.to]=dis[x]+1;
        que.push(t.to);
      }
    }
  }
  return dis[t];
}
int dfs(int x,int a){
    if(x==t||a==0) return a;
    int fl=0,c;
    for(int &i=cur[x];i<g[x].size();i++){
       edge &t=edges[g[x][i]];
       if(dis[t.to]==dis[x]+1&&(c=dfs(t.to,min(a,t.cup-t.flow)))){
            t.flow+=c;
            edges[g[x][i]^1].flow-=c;
         fl+=c;
            a-=c;
       } 
       if(a==0) break;
    }
    return fl;
}
void Dinic(int s,int t){
    while(bfs(s,t)){
     memset(cur,0,sizeof(cur));
     ans+=dfs(s,INF);
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    s=0; t=n+1;
    for(int i=1;i<=m;i++){
        scanf("%d%d%d%d",&x,&y,&d,&u);
        add(x,y,u-d);
        tmp.push_back(edges.size()-2);
        dow[i]=d;
        du[y]+=d; du[x]-=d;
    }
    for(int i=1;i<=n;i++){
        if(du[i]>0) add(s,i,du[i]);
        else add(i,t,-du[i]);
    }
    Dinic(s,t);
    int hhh=g[0].size(),flag=1;
    for(int i=0;i<hhh;i++){
        edge ee=edges[g[0][i]];
        if(ee.flow<ee.cup ) {flag=0;break;}  
    }
    if(!flag) printf("NO
");
    else{
        printf("YES
");
        hhh=tmp.size(); int cnt=0;
        for(int i=0;i<hhh;i++){
        edge ee=edges[tmp[i]];
        printf("%d
",ee.flow+dow[++cnt]);
        }
    }
    return 0;
}

 

说一下有上下界的网络流

我们嫌下界麻烦，就要把它弄掉（YK说），于是我们把每条弧的容量变成上界减下界

之后为了满足流量守恒定理，个人的理解是，一条从u到v的弧，u点少流出了down那么多，就直接从它到汇点加一条容量为down的弧，v点少流入了down，就从源点向它流加一条容量为-down的弧

做法是对于每个点先把它流出的和流入的down统计一下，最后再加弧

 

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#include<vector>
const int maxn=2050;
const int INF=1e9+7;
int f,s=0,t=201,ans,n,m,a,b,pre[maxn],fl[maxn],ad[maxn];
using namespace std;
struct edge{
    int from,to,cup,flow;
    edge(int from,int to,int cup,int flow):from(from),to(to),cup(cup),flow(flow){}
};
vector<edge>edges;
vector<int>g[202];
void add(int u,int v,int c){
    edges.push_back(edge(u,v,c,0));
    edges.push_back(edge(v,u,0,0));
    int t=edges.size();
    g[u].push_back(t-2);
    g[v].push_back(t-1);   
}
queue<int>que;
int bfs(int s,int e){
    while(!que.empty() ) que.pop() ;
    memset(fl,0,sizeof(fl));
    fl[s]=INF;
    que.push(s);
    while(!que.empty() ){
    int x=que.front();que.pop();
     for(int i=0;i<g[x].size();i++){
         int xxx=g[x][i];
        edge t=edges[g[x][i]];
        if(!fl[t.to]&&t.flow<t.cup ){
          fl[t.to]=min(fl[x],t.cup-t.flow);
          pre[t.to]=g[x][i];
          if(fl[e]) return fl[e];
          que.push(t.to);
        }        
      }
    }
    return 0;
}
void EK(){
    while(f=bfs(s,t)){
       ans+=f;
       for(int i=pre[t];;i=pre[edges[i].from]){
          edges[i].flow+=f;
          edges[i^1].flow-=f;
          int l=edges[2].from;
          if(edges[i].from==s) break;
       }
         /*for(int i=0;i<edges.size();i++){
   cout<<i<<":"<<" ";
   int o=edges[i].from; cout<<o<<" ";
   o=edges[i].to; cout<<o<<" ";
   o=edges[i].cup; cout<<o<" ";
   o=edges[i].flow; cout<<""<<o<<endl;
   }
    int aa;
    aa++;*/
    }
}
int main()
{
   scanf("%d%d",&m,&n);
   for(;;){
     scanf("%d%d",&a,&b);
     if(a==-1&&b==-1) break;
     if(!ad[a]) add(s,a,1),ad[a]=1; 
     add(a,b+100,1);
     if(!ad[b+100]) add(b+100,t,1),ad[b+100]=1;
   }/*
   for(int i=0;i<edges.size();i++){
   cout<<i<<":"<<" ";
   int o=edges[i].from; cout<<o<<" ";
   o=edges[i].to; cout<<o<<" ";
   o=edges[i].cup; cout<<o<" ";
   o=edges[i].flow; cout<<o<<endl;
   }*/
   EK();
   printf("%d
",ans);
   for(int i=0;i<edges.size();i++){
     edge x=edges[i];
     if(x.from !=s&&x.to !=t&&x.cup&&x.flow==x.cup){
         printf("%d %d
",x.from,x.to-100);
     }
   }
   return 0;
}

 

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;
const int maxn=420;
const int INF=0x7fffffff;
int inline read(){
    char ch=getchar(); int f=1,ret=0;
    while(ch>'9'||ch<'0') {if(ch=='-') f=-1; ch=getchar();}
    for(;ch>='0'&&ch<='9';ch=getchar()) ret=ret*10+ch-'0';
    return ret*f;
}
struct edge{
    int v,w,next;
}e[maxn];
int n,m,fir[maxn],dis[maxn];
int cnt=0;
int add(int u,int v,int w){
    e[cnt].v =v;e[cnt].w =w; e[cnt].next =fir[u]; fir[u]=cnt++;
    e[cnt].v =u;e[cnt].w =0; e[cnt].next =fir[v]; fir[v]=cnt++;
}
queue<int>q;
int bfs(){
    memset(dis,0,sizeof(dis));
    dis[1]=1; q.push(1);
    while(!q.empty()){
        int u=q.front() ;q.pop();
        for(int i=fir[u];i!=-1;i=e[i].next ){
            if(dis[e[i].v ]==0&&e[i].w ){
                dis[e[i].v]=dis[u]+1;
                q.push(e[i].v);
            }
        }
    }
    return dis[n];
}

int dfs(int s,int limit){
    if(s==n) return limit;
    int cost=0,tmp=0;
    for(int i=fir[s];i!=-1;i=e[i].next ){
        if(e[i].w &&dis[e[i].v]==dis[s]+1){
             tmp=dfs(e[i].v ,min(limit-cost,e[i].w));
             if(tmp!=0){
                 e[i].w -=tmp;e[i^1].w+=tmp;cost+=tmp;if(cost==limit) break;
          }
          else dis[e[i].v ]=-1;
        }
    }
    return cost;
}

int dinic(){
    int ans=0;
    while(bfs())
      ans+=dfs(1,INF);
    return ans;
}

int main()
{
    memset(fir,-1,sizeof(fir));
    m=read(); n=read();
    for(int i=1;i<=m;i++){
        int u,v,w;
        u=read();v=read();w=read();
        add(u,v,w);
    }
    printf("%d",dinic());    
    return 0;
}

 

 

一些题

1.最小割 tyvj P1338 QQ农场

http://www.tyvj.cn/p/1338

对于每个点摘它就不能摘它周围四个，可以明显看出这是一个二分图，然后sum-最小割就是答案。

//Twenty
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
const int maxn=299*299;
const int INF=0x7fffffff;
int ans,s=0,sum,t,n,a[maxn],dis[maxn],cur[maxn],x,y;
struct edge{
    int from,to,flow,cup;
    edge(int from,int to,int flow,int cup):from(from),to(to),flow(flow),cup(cup){}
};
vector<edge>edges;
vector<int>g[maxn];
void add(int u,int v,int w){
   edges.push_back(edge(u,v,0,w));
   edges.push_back(edge(v,u,0,0));
   int t=edges.size();
   g[u].push_back(t-2);
   g[v].push_back(t-1);
} 
queue<int>que;
int bfs(int s,int t){
  memset(dis,0,sizeof(dis));
  dis[s]=1;
  que.push(s);
  while(!que.empty() ){
    int x=que.front();que.pop() ;
    for(int i=0;i<g[x].size();i++){
      edge t=edges[g[x][i]];
      if(!dis[t.to]&&t.cup>t.flow){
        dis[t.to]=dis[x]+1;
        que.push(t.to);
      }
    }
  }
  return dis[t];
}
int dfs(int x,int a){
    if(x==t||a==0) return a;
    int fl=0,c;
    for(int &i=cur[x];i<g[x].size();i++){
       edge &t=edges[g[x][i]];
       if(dis[t.to]==dis[x]+1&&(c=dfs(t.to,min(a,t.cup-t.flow)))){
            t.flow+=c;
            edges[g[x][i]^1].flow-=c;
         fl+=c;
            a-=c;
       } 
       if(a==0) break;
    }
    return fl;
}
void Dinic(int s,int t){
    while(bfs(s,t)){
     memset(cur,0,sizeof(cur));
     ans+=dfs(s,INF);
    }
}
int check(int i,int j){
    y=(i-1)*n+j;
    return (i>=1&&i<=n&&j>=1&&j<=n);
}
int main()
{
    scanf("%d",&n);
    t=n*n+1;
    for(int i=1;i<=n;i++){
        int flag=i;
    for(int j=1;j<=n;j++){
        x=(i-1)*n+j;
        scanf("%d",&a[x]);
        sum+=a[x];
        if(flag%2){
        if(check(i+1,j)) 
         add(x,y,INF); 
        if(check(i-1,j)) 
         add(x,y,INF);
        if(check(i,j+1)) 
         add(x,y,INF);
        if(check(i,j-1)) 
         add(x,y,INF);
         add(s,x,a[x]);
        }
        else add(x,t,a[x]);
        ++flag;
    }
    }
    Dinic(s,t);
    printf("%d
",sum-ans);
    return 0;
}

 

2.BZOJ 1834网络扩容

先求出最大流，然后每条弧上再加一条容量为INF费用为扩容费用的弧，从源点流入需要扩容的大小，跑一遍费用流。

//Twenty
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
const int INF=0x7fffffff;
const int maxn=(5000+29)*2; 
int nowfl,aa,b,c,d,n,m,k,dis[maxn],cur[maxn],s,t,ans1,ans2,vis[maxn],woc;
int ps[maxn][3],a[maxn],pre[maxn];
struct edge{
    int from,to,flow,cup,cost;
    edge(int from,int to,int flow,int cup,int cost):from(from),to(to),flow(flow),cup(cup),cost(cost){}
};
vector<edge>edges;
vector<int>g[maxn];
void add(int u,int v,int w,int cost){
   edges.push_back(edge(u,v,0,w,cost));
   edges.push_back(edge(v,u,0,0,-cost));
   int t=edges.size();
   g[u].push_back(t-2);
   g[v].push_back(t-1);
} 
queue<int>que;
int bfs(int s,int t){
  memset(dis,0,sizeof(dis));
  dis[s]=1;
  que.push(s);
  while(!que.empty() ){
    int x=que.front();que.pop() ;
    for(int i=0;i<g[x].size();i++){
      edge t=edges[g[x][i]];
      if(!dis[t.to]&&t.cup>t.flow){
        dis[t.to]=dis[x]+1;
        que.push(t.to);
      }
    }
  }
  return dis[t];
}
int dfs(int x,int a){
    if(x==t||a==0) return a;
    int fl=0,c;
    for(int &i=cur[x];i<g[x].size();i++){
       edge &t=edges[g[x][i]];
       if(dis[t.to]==dis[x]+1&&(c=dfs(t.to,min(a,t.cup-t.flow)))){
            t.flow+=c;
            edges[g[x][i]^1].flow-=c;
         fl+=c;
            a-=c;
       } 
       if(a==0) break;
    }
    return fl;
}
void Dinic(int s,int t){
    while(bfs(s,t)){
     memset(cur,0,sizeof(cur));
     ans1+=dfs(s,INF);
    }
}
int spfa(int s,int t){
    memset(vis,0,sizeof(vis));
    memset(dis,127,sizeof(dis));
    memset(a,0,sizeof(a));
    que.push(s); vis[s]=1; dis[s]=0; a[s]=woc;
    while(!que.empty() ){
        int x=que.front() ;que.pop() ;
        vis[x]=0;
        for(int i=0;i<g[x].size();i++){
            edge now=edges[g[x][i]];
            if(now.flow<now.cup&&dis[now.to ]>dis[now.from ]+now.cost ){
                dis[now.to ]=dis[now.from ]+now.cost ;
                a[now.to]=min(a[now.from],now.cup-now.flow); 
                pre[now.to]=g[x][i];
                if(!vis[now.to ]){
                    vis[now.to]=1;
                    que.push(now.to); 
                }
            }
        }
    }
    return a[t];     
}
void EK(int s,int t)
{
    woc=k;
    while(woc&&spfa(s,t)){
        for(int i=t;i!=s;i=edges[pre[i]].from){
           edges[pre[i]].flow+=a[t];
           edges[pre[i]^1].flow-=a[t];
        }
        woc-=a[t];
        ans2+=(dis[t]*a[t]);
    }
}
int main()
{
    scanf("%d%d%d",&n,&m,&k);
    s=1,t=n;
    for(int i=1;i<=m;i++){
    scanf("%d%d%d%d",&aa,&b,&c,&d);
    ps[i][0]=aa; ps[i][1]=b; ps[i][2]=d;
    add(aa,b,c,0);
    }
    Dinic(s,t);
    printf("%d ",ans1);
    for(int i=1;i<=m;i++)
    add(ps[i][0],ps[i][1],INF,ps[i][2]);
    EK(s,t);
    printf("%d
",ans2);
    return 0;
}

 

3.codevs 1227 方格取数

最大费用流

要求取m次，拆点，每个点向虚点之间连两条边，一条控制联通，容量为INF，费用为0，一条控制费用，容量为1,。然后每个点向能到达的点连容量为m的边，源点向起点连容量为m的边。

//Twenty
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#include<vector>
const int INF=0x7fffffff;
const int maxn=105*105;
using namespace std;
int b[maxn],n,m,xx,yy,zz,cur[maxn],s,t,dis[maxn],vis[maxn],a[maxn],pre[maxn];
int vv,ansv,ansf;
using namespace std;
struct edge{
    int from,to,cup,flow,val;
    edge(int from,int to,int cup,int flow,int val):from(from),to(to),cup(cup),flow(flow),val(val){}
};
vector<int>g[maxn];
vector<edge>edges;
void add(int from,int to,int cup,int val){
    edges.push_back(edge(from,to,cup,0,val));
    edges.push_back(edge(to,from,0,0,-val));
    int x=edges.size();
    g[from].push_back(x-2);
    g[to].push_back(x-1); 
}
queue<int>que;
int spfa(int s,int t){
    memset(vis,0,sizeof(vis));
    memset(dis,127,sizeof(dis));
    memset(a,0,sizeof(a));
    que.push(s); vis[s]=1;dis[s]=0;a[s]=1e9;
    while(!que.empty() ){
        int x=que.front() ;que.pop() ;
        vis[x]=0;
        for(int i=0;i<g[x].size();i++){
            edge now=edges[g[x][i]];
            if(now.flow<now.cup&&dis[now.to ]>dis[now.from ]+now.val ){
                dis[now.to ]=dis[now.from ]+now.val ;
                a[now.to]=min(a[now.from],now.cup-now.flow); 
                pre[now.to]=g[x][i];
                if(!vis[now.to ]){
                    vis[now.to]=1;
                    que.push(now.to); 
                }
            }
        }
    }
    return a[t];     
}
void EK(int s,int t)
{
    while(spfa(s,t)){
        for(int i=t;i!=s;i=edges[pre[i]].from){
           edge &ee=edges[pre[i]];
           ee.flow+=a[t];
           edges[pre[i]^1].flow-=a[t];
        }
        ansv+=(dis[t]*a[t]);
    }
}
int check(int i,int j){
    vv=(i-1)*n+j;
    return (i>=1&&i<=n&&j>=1&&j<=n);
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++){
        scanf("%d",&b[(i-1)*n+j]);
        b[(i-1)*n+j]*=-1;
    }
    s=1,t=n*n+n*n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            {
                int uu=(i-1)*n+j;
                if(uu==1) add(uu,uu+n*n,m,0);
                else {add(uu,uu+n*n,INF,0);
                add(uu,uu+n*n,1,b[uu]);}
                if(check(i+1,j)) 
                    add(uu+n*n,vv,m,0);
                if(check(i,j+1)) 
                    add(uu+n*n,vv,m,0);
            }
    EK(s,t);
    if(m==0) printf("0
");
    else
    printf("%d
",(ansv+b[1])*-1);
    return 0;
}

4.codevs 1022 覆盖

http://codevs.cn/problem/1022/

二分图匹配水题 显然图是二分图 每个点判断一下可不可覆盖（是不是水塘）。

//Twenty
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
const int maxn=105*105;
const int INF=0x7fffffff;
int s=0,t,n,m,k,a[maxn],ans,dis[maxn],cur[maxn],x,y,u,v,flag;
struct edge{
    int from,to,flow,cup;
    edge(int from,int to,int flow,int cup):from(from),to(to),flow(flow),cup(cup){}
};
vector<edge>edges;
vector<int>g[maxn];
void add(int u,int v,int w){
   edges.push_back(edge(u,v,0,w));
   edges.push_back(edge(v,u,0,0));
   int t=edges.size();
   g[u].push_back(t-2);
   g[v].push_back(t-1);
} 
queue<int>que;
int bfs(int s,int t){
  memset(dis,0,sizeof(dis));
  dis[s]=1;
  que.push(s);
  while(!que.empty() ){
    int x=que.front();que.pop() ;
    for(int i=0;i<g[x].size();i++){
      edge t=edges[g[x][i]];
      if(!dis[t.to]&&t.cup>t.flow){
        dis[t.to]=dis[x]+1;
        que.push(t.to);
      }
    }
  }
  return dis[t];
}
int dfs(int x,int a){
    if(x==t||a==0) return a;
    int fl=0,c;
    for(int &i=cur[x];i<g[x].size();i++){
       edge &t=edges[g[x][i]];
       if(dis[t.to]==dis[x]+1&&(c=dfs(t.to,min(a,t.cup-t.flow)))){
            t.flow+=c;
            edges[g[x][i]^1].flow-=c;
         fl+=c;
            a-=c;
       } 
       if(a==0) break;
    }
    return fl;
}
void Dinic(int s,int t){
    while(bfs(s,t)){
     memset(cur,0,sizeof(cur));
     ans+=dfs(s,INF);
    }
}
int check(int i,int j){
    v=(i-1)*m+j;
    return (!a[v]&&i>=1&&i<=n&&j>=1&&j<=n);
}
int main()
{
    scanf("%d%d%d",&n,&m,&k);
    t=n*m+1;
    for(int i=1;i<=k;i++){
        scanf("%d%d",&x,&y);
        a[(x-1)*m+y]=1;
    } 
    for(int i=1;i<=n;i++)
     {flag=i;
     for(int j=1;j<=m;j++){
        u=(i-1)*m+j;
        if(!a[u]&&flag%2){
          if(check(i+1,j)) 
             add(u,v,INF); 
          if(check(i-1,j)) 
             add(u,v,INF);
          if(check(i,j+1)) 
             add(u,v,INF);
          if(check(i,j-1)) 
             add(u,v,INF);
          add(s,u,1);
        }
        else if(!a[u]) 
            add(u,t,1);
        ++flag;
     }
     }
    Dinic(s,t);
    printf("%d
",ans);
    return 0;
}

 

5.最小路径覆盖问题

先把每个点单独为一条路径，将两条路径连起来就可以减少一条路径，考虑将哪些点连起来，把所有点增加一个，分为两份，就成了二分图匹配问题，就可以用网络流搞了。

//Twenty
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
const int maxn=30000+5;
const int INF=0x7fffffff;
int ans,n,m,x,y,cur[maxn],s,t,dis[maxn],ts,in[maxn],p[maxn];
int a[maxn],nx[maxn],qq[maxn];
struct edge{
    int from,to,flow,cup;
    edge(int from,int to,int flow,int cup):from(from),to(to),flow(flow),cup(cup){}
};
vector<edge>edges;
vector<int>g[maxn];
void add(int u,int v,int w){
   edges.push_back(edge(u,v,0,w));
   edges.push_back(edge(v,u,0,0));
   int t=edges.size();
   g[u].push_back(t-2);
   g[v].push_back(t-1);
   edge ee=edges[t-1];
   int xxxx=1;
   xxxx++;
} 
queue<int>que;
int bfs(int s,int t){
    memset(a,0,sizeof(a));
    while(!que.empty()) que.pop();
    que.push(s);
    a[s]=1e9;
    while(!que.empty() ){
        int x=que.front();que.pop();
        for(int i=0;i<g[x].size() ;i++){
            edge tep=edges[g[x][i]];
            if(!a[tep.to ]&&tep.cup >tep.flow ){
            a[tep.to ]=min(a[x],tep.cup -tep.flow );
            p[tep.to ]=g[x][i];
                que.push(tep.to );
            }
        }
        if(a[t]) return 1;
    } 
    return 0;
}
int EK(int s,int t){
    ans=0;
    while(bfs(s,t)){
        for(int i=t;i!=s;i=edges[p[i]].from){
            edges[p[i]].flow+=a[t];
            edges[p[i]^1].flow-=a[t];
        }
        ans+=a[t];
    }
    return ans;
}
void printedge(){
    for(int i=0;i<edges.size();i++){
        edge ee=edges[i];
        printf("【%d】
",i+1);
        printf("from: %d
",ee.from);
        printf("to: %d
",ee.to);
        printf("flow: %d
",ee.flow);
        printf("cup: %d
",ee.cup);
    }
} 
void print(){
    int hhh=edges.size();
    for(int i=0;i<hhh;i++){
        edge ee=edges[i];
        if(ee.from>=1&&ee.from<=n&&ee.to>=n+1&&ee.to<=n+n&&ee.flow==1){
            nx[ee.from]=ee.to-n;
            in[ee.to-n]++;
        }
    }
    for(int i=1;i<=n;i++)
        if(!in[i]){
            int tmp=i;
            printf("%d ",tmp);
            while(nx[tmp]){
                 printf("%d ",nx[tmp]);
                 tmp=nx[tmp];
            }
            printf("
");
        }
}
int main()
{
    scanf("%d%d",&n,&m);
    s=0;t=n*n+1;
    for(int i=1;i<=n;i++)
    {add(s,i,1);
    add(i+n,t,1);}
    for(int i=1;i<=m;i++){
    scanf("%d%d",&x,&y);
    add(x,y+n,1); 
    }
    EK(s,t);
    ts=n-ans;
    print();
    printf("%d
",ts);
    return 0;
}

 

6.BZOJ 1305 Dance跳舞

http://www.lydsy.com/JudgeOnline/problem.php?id=1305

首先男生女生可以看做一个二分图，每个人有喜欢的人和不喜欢的人，显然可以拆点，我们把喜欢的叫真的点，不喜欢的叫假的点。

每个人最大可以忍受不喜欢的人的个数m,从每个真男孩向假男孩连容量为m的点，从每个假女孩向真女孩连容量为m的边。相互喜欢的真男孩连向真女孩容量为1的边。

然后二分答案，二分一个最大可以跳的场数k，从源点向每个真男孩连容量为k的边，每个真女孩向汇点连容量为k的边，跑一遍最大流，检查每条连向汇点的边是否满流。

//Twenty
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#include<vector>
const int maxn=205*205;
const int INF=0x7fffffff;
int n,k,a[55][55],l=0,r=50;
char ch[maxn];
using namespace std;
int s,t,ans,cur[maxn],dis[maxn],cs;
struct edge{
    int from,to,flow,cup;
    edge(int from,int to,int flow,int cup):from(from),to(to),flow(flow),cup(cup){}
};
vector<edge>edges;
vector<int>g[maxn];
void add(int u,int v,int w){
   edges.push_back(edge(u,v,0,w));
   edges.push_back(edge(v,u,0,0));
   int t=edges.size();
   g[u].push_back(t-2);
   g[v].push_back(t-1);
} 
queue<int>que;
int bfs(int s,int t){
  memset(dis,0,sizeof(dis));
  dis[s]=1;
  que.push(s);
  while(!que.empty() ){
    int x=que.front();que.pop() ;
    for(int i=0;i<g[x].size();i++){
      edge t=edges[g[x][i]];
      if(!dis[t.to]&&t.cup>t.flow){
        dis[t.to]=dis[x]+1;
        que.push(t.to);
      }
    }
  }
  return dis[t];
}
int dfs(int x,int a){
    if(x==t||a==0) return a;
    int fl=0,c;
    for(int &i=cur[x];i<g[x].size();i++){
       edge &t=edges[g[x][i]];
       if(dis[t.to]==dis[x]+1&&(c=dfs(t.to,min(a,t.cup-t.flow)))){
            t.flow+=c;
            edges[g[x][i]^1].flow-=c;
         fl+=c;
            a-=c;
       } 
       if(a==0) break;
    }
    return fl;
}
void Dinic(int s,int t){
    while(bfs(s,t)){
     memset(cur,0,sizeof(cur));
     ans+=dfs(s,INF);
    }
}
int check(int x){
    int hhh=edges.size() ;
    for(int i=0;i<hhh;i++){
        edge &ee=edges[i];
        ee.flow=0;
        if(ee.from==s) {
            if(ee.to<=n)
                ee.cup=x;
            else ee.cup=0;
        }
        if(ee.to==t) {
            if(ee.from>=2*n+1&&ee.from<=3*n)
                {ee.cup=x;
                 int debugg=1;
                 debugg++;
                 }
            else ee.cup=0;
        }
    }
    ans=0;
    Dinic(s,t);
    return (ans>=n*x);
}
int main()
{
    scanf("%d%d",&n,&k);
    t=n*4+1;
    for(int i=1;i<=n;i++){
        scanf("%s",ch);
        for(int j=0;j<n;j++)
            if(ch[j]=='Y') a[i][j+1]=1; 
    }
    for(int i=1;i<=n;i++){
        add(s,i,0);   
        add(i,n+i,k); //1~n 真男孩 n~2n 假男孩 
        add(2*n+i,t,0); 
        add(3*n+i,2*n+i,k); //2n~3n 真女孩 3n~4n 假女孩 
        for(int j=1;j<=n;j++){
            if(a[i][j]) add(i,2*n+j,1);   
            else add(n+i,3*n+j,1);
        }
    }
    //if(!check(1)) printf("0
");
    //else{
        while(l<=r){
            int mid=(l+r)>>1;
            if(check(mid)) cs=mid,l=mid+1;
            else r=mid-1;
        //}
        }
    printf("%d
",cs);    
    return 0;
}

 

7.BZOJ 2127 happiness

http://www.lydsy.com/JudgeOnline/problem.php?id=2127

很经典的文理分科问题，一开始瘦学长直接抬出了一个图，非常懵逼，后来问了YYH大神才懂了

首先这是一个二分图，然后这是一个最小割，因为可以容易地发现要么同选文，要么同选理，要么一文一理，所以A选文 A选理 B选文 B选理 同选文 同选理6条边中我们要割去一些边，并且使得割去的边之和最小，就是一个最小割模型了。

那么如何建图呢，

YYH 说 我们不要去考虑它剩下的是什么，只考虑割去的是什么。（也因此中间要建成双向边）

就有了如下的图，可以自己沿着所以可行的割割一遍，

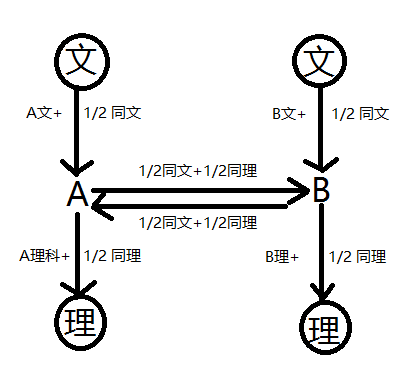（注：两个文两个理其实是一个点 源点和汇点）

 

实际操作的时候，我们把边的容量都乘以2，最后再除以二得出答案。

//Twenty
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
const int maxn=105*105;
const int INF=0x7fffffff;
int n,m,x,s,t,cur[maxn],uu,vv;
int jz[7][maxn],ans,dis[maxn],sum;
struct edge{
    int from,to,flow,cup;
    edge(int from,int to,int flow,int cup):from(from),to(to),flow(flow),cup(cup){}
};
vector<edge>edges;
vector<int>g[maxn];
void add(int u,int v,int w){
   edges.push_back(edge(u,v,0,w));
   edges.push_back(edge(v,u,0,0));
   int t=edges.size();
   g[u].push_back(t-2);
   g[v].push_back(t-1);
} 
queue<int>que;
int bfs(int s,int t){
  memset(dis,0,sizeof(dis));
  dis[s]=1;
  que.push(s);
  while(!que.empty() ){
    int x=que.front();que.pop() ;
    for(int i=0;i<g[x].size();i++){
      edge t=edges[g[x][i]];
      if(!dis[t.to]&&t.cup>t.flow){
        dis[t.to]=dis[x]+1;
        que.push(t.to);
      }
    }
  }
  return dis[t];
}
int dfs(int x,int a){
    if(x==t||a==0) return a;
    int fl=0,c;
    for(int &i=cur[x];i<g[x].size();i++){
       edge &t=edges[g[x][i]];
       if(dis[t.to]==dis[x]+1&&(c=dfs(t.to,min(a,t.cup-t.flow)))){
            t.flow+=c;
            edges[g[x][i]^1].flow-=c;
         fl+=c;
            a-=c;
       } 
       if(a==0) break;
    }
    return fl;
}
void Dinic(int s,int t){
    while(bfs(s,t)){
     memset(cur,0,sizeof(cur));
     ans+=dfs(s,INF);
    }
}
int check(int i,int j){
    vv=(i-1)*n+j;
    return (i>=1&&i<=n&&j>=1&&j<=m);
}
int main()
{
    scanf("%d%d",&n,&m);
    s=0;t=n*m+1;
    for(int tt=1;tt<=6;tt++){
    for(int i=1;i<=n;i++){
    if((tt==3||tt==4)&&i==n) continue;
    for(int j=1;j<=m;j++){
        if((tt==5||tt==6)&&j==m) continue;
        int u=(i-1)*n+j;
        scanf("%d",&jz[tt][u]);
        sum+=jz[tt][u];
    }
    }
    }
    for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++){
        uu=(i-1)*n+j;
        int tw=0,tl=0;
        if(check(i+1,j)){
            int tmp=jz[3][uu]+jz[4][uu];
            add(uu,vv,tmp); 
            add(vv,uu,tmp); 
            tw+=jz[3][uu]; tl+=jz[4][uu];
        }
        if(check(i-1,j)){
            tw+=jz[3][vv]; tl+=jz[4][vv];
        }
        if(check(i,j+1)){
            int tmp=(jz[5][uu]+jz[6][uu]);
            add(uu,vv,tmp);
            add(vv,uu,tmp);
            tw+=jz[5][uu]; tl+=jz[6][uu];
        }
        if(check(i,j-1)){
            tw+=jz[5][vv]; tl+=jz[6][vv];
        }
        //if(i*j%2){
            //add(s,uu,jz[2][uu]+tl);
            //add(uu,t,jz[1][uu]+tw);
        //}
        //else{
            add(s,uu,jz[1][uu]*2+tw); 
            add(uu,t,jz[2][uu]*2+tl);
        //}
           //用Double会出问题，所以都乘2 
           //建图关键不在如何流而在割去的是什么 
           //sum为五部分之和，割去相应的边方案要合法 
    }
    Dinic(s,t);
    printf("%d",sum-ans/2);
    return 0;
}