曦皓的算式

【题目描述】

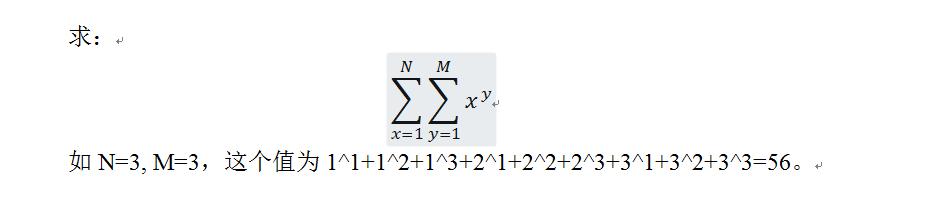
【输入描述】

输入两个数N和M。

【输出描述】

输出一个数，表示答案 mod (10⁹+7)的值。

【输入样例】

3 3

【输出样例】

56

【数据范围及提示】

对于50%的数据，1 ≤ N,M ≤ 1000；

对于100%的数据，1 ≤ N,M ≤ 50000。

源代码：

#include<cstdio>
#define LL long long //LL上瘾。
#define INF 1000000007
LL n,m;
LL Count(LL X,LL S)
{
    LL Number=1;
    while (S)
    {
        if (S&1)
          Number=Number*X%INF;
        X=X*X%INF;
        S>>=1;
    }
    return Number;
}
int main()
{
    scanf("%I64d%I64d",&n,&m);
    LL Ans=m;
    for (LL a=2;a<=n;a++)
    {
        LL t=a;
        t=t*((Count(a,m)-1+INF)%INF)%INF;
        t=t*Count(a-1,INF-2)%INF;
        Ans=(Ans+t)%INF;
    }
    printf("%I64d",Ans);
    return 0;
}

/*
    一道警醒世人的题。
    利用高中数学的等比数列就可以O(n)解得答案。
    做题还是要灵活运用，NOIP的知识点边框不要卡得太死。
    终于会乘法逆元了！那幸福的逆元告诉我的，我将告诉每一个模。
    乘法逆元：
        对于两个数A、B，若有Ax≡1(mod B)，那么x就叫做A对B的乘法逆元。
    作用：
        举个例子：
            12/4 mod 7=3
            用乘法逆元转化一下，对于(4,7)的乘法逆元为2（4*2≡1(mod 7)），则有：
                12*2 mod 7=3
            这样，除法就变为了乘法。
        但是有一点，(A,B)应互素，否则不存在逆元，不过一般NOIP都给素数。
    怎么求？
    利用费马小定理：
        a^(p-1)≡1(mod p)（p为素数）
        a*a^(p-2)≡1(mod p)
        那a^(p-2)不就是(a,p)的逆元嘛，快速幂解决。
*/