注:本节主要讨论最大堆(最小堆同理)。
一、堆的概念
堆,又称二叉堆。同二叉查找树一样,堆也有两个性质,即结构性和堆序性。
1、结构性质:
堆是一棵被完全填满的二叉树,有可能的例外是在底层,底层上的元素从左到右填入。这样的树称为完全二叉树(complete binary tree)。下图就是这样一个例子。

对于完全二叉树,有这样一些性质:
(1)、一棵高h的完全二叉树,其包含2^h ~ (2^(h+1) - 1)个节点。也就是说,完全二叉树的高是[logN],显然它是O(logN)。
(2)、完全二叉树可以用数组进行结构表示:
index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
value | A | B | C | D | E | F | G | H | I | J |
仔细考察该数组的index和元素在树中的分布情况,可以得到:
对于一个三元素的二叉树,树结构和数组索引有如下关系:
leftChild.index = 2 * parent.index;
rightChild.index = 2 * parent.index + 1;
(3)、通过前面的讨论,我们可以这样去看待一个堆的数据结构:
一个数组、当前堆的大小heapLen。
2、堆序性质:
使操作被快速执行的性质是堆序性(heap order)。
堆序性质:在一个堆中,对于每一个节点x,x的父亲中的关键字大于(或等于)x中的关键字,根节点除外(它没有父节点)。
根据堆序性质,最大元总可以在根处找到。因此,我们以常数时间完成查找操作。
比较:
堆序性质的堆:
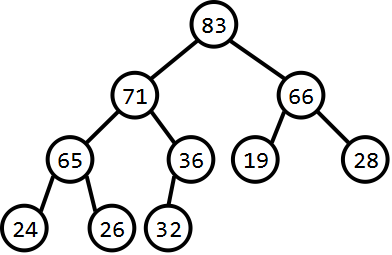
无堆序性质的堆:

二、基本堆操作
声明:
int heap[MAX+1];
int heapLen; //堆的大小
int leftEle(int i){ return i*2; }
int rightEle(int i){ return i*2+1; }
int parentEle(int i){ return i/2; }
void swap(int i, int j){
int tmp;
tmp = i, i = j, j = tmp;
}
1、查询操作:
int findMax()
{
return heap[1];
}
函数解析:
堆的最大值即为根节点元素,直接返回该值即可。
下沉操作:
在给出具体如何建堆的操作之前,我们可以考察一下具体应该怎样去实现。
2、堆维护操作:
下沉操作:
void maxHeapify(int i)
{
int iLeft = leftEle(i); //找到该节点的左儿子
int iRight = rightEle(i); //找到该节点的右儿子
int largest = i; //记录最大值节点,初始为节点自己
//找到最大值对应的节点
if( iLeft < heapLen && heap[i] < heap[iLeft] )
largest = iLeft;
if(iRight < heapLen && heap[largest] < heap[iRight] )
largest = iRight;
//交换原节点与最大值对应的节点,然后对交换后的节点进行堆维护操作
if(largest != i)
{
swap(heap[i], heap[largest]);
maxHeapify(largest);
}
}
3、建堆操作:
在给出具体如何建堆的操作之前,我们可以考察一下具体应该怎样去实现。
现在给出一个堆(应该不能称之为堆),这个堆由初始数组构造而成,其结构为:

显然这不是最大堆。
整个数组为:
index | 83 | 11 | 6 | 15 | 36 | 19 |
value | 1 | 2 | 3 | 4 | 5 | 6 |
经过一系列的操作,我们需要将该堆转换为:

整个最大堆化过程是这样的:自下而上逐层维护堆操作。
首先,找到第一个有子树的节点,对该节点进行堆维护操作,然后依次向上,进行堆维护。
这里的问题:
第一个有子树的节点在哪里?
===>>>>>
对于完全二叉树,叶子节点必然存放在数组的尾端,现在的问题就在于叶子节点到底有多少个?知晓叶子节点的个数后,就可以很容易地确定有子树节点的位置。那么叶子节点到底有多少个呢?
设完全二叉树总共有n个节点,叶子节点有n0个,由于二叉树的节点的度数最大为2,于是可设度数为1的节点数为n1,度数为2的节点数为n2。
于是我们可以得到这样几个关系式:
n0+n1+n2 = n;
n-1 = 2*n2 + n1;(边数的两种不同表示方式)
解此方程式,可以得到:
n0 = (n+1-n1)/2.
对于完全二叉树,n1 = 1或0
当n1=1时,n0=n/2;当n1=0时,n0=(n+1)/2。
于是我们可以得到叶子节点为总节点数的一半。
从而有,非叶子节点应该是数组的前半部分。
===>>>
void buildHeap()
{
int i;
for( i = heapLen/2; i > 0; i--)
maxHeapify(i);
}
堆排序的关键在于将最大值元素交换到数组尾端,重新进行堆维护操作。依次循环操作,即可以得到排序的数组。
4、排序操作:
堆排序的关键在于将最大值元素交换到数组尾端,重新进行堆维护操作。依次循环操作,即可以得到排序的数组。
void heapSort()
{
int i;
buileHeap();
for( i=heapLen; i>=1; i--)
{
swap(heap[heapLen], heap[1]);
heapLen--;
maxHeapify(1);
}
}
函数解析:
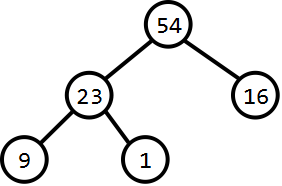
首先我们先利用堆排序对一数组中的元素进行排序:
23 | 1 | 16 | 9 | 54 |

现在进行堆排序:
a、建堆:
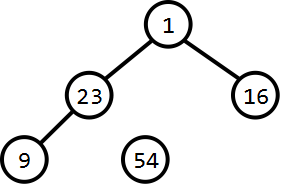
b、交换54和1,并解除堆最后一个元素与原堆的关系:
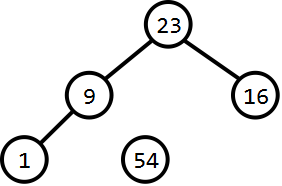
c、重构堆:
d、依次循环最终得到:

这样,数组变为:
1 | 9 | 16 | 23 | 54 |
5、插入元素操作:
插入insertHeap():该操作同优先队列(priority queue)中的push操作。
在介绍具体的插入操作前,需要实现increaseKey(int i, int key)函数,用于更新堆结构。
上浮操作:
void increaseKey(int i, int key)
{
assert(key >= heap[i]); //断言key值大于heap[i],如果不成立,则终止并报错
heap[i] = key;
while(i > 1 && heap[parentEle(i)] < heap[i])
{
swap(heap[i], heap[parentEle(i)]);
i = parentEle(i);
}
}
在这里,需要着重介绍一下increaseKey操作的具体步骤,举例说明:
对于这样一个堆,将节点6的值由8增加到54—>>>:

整个操作过程即为increaseKey(6, 54)。
整个过程如下:

于是,插入元素到堆的代码如下:
void insertHeap( int x )
{
heapLen++;
heap[heapLen] = -INF;
increaseKey(heapLen, x);
}
6、删除元素操作:
删除deleteHeapMax():相当于优先队列中的pop()操作。
int deleteHeapMax()
{
int ret = heap[1];
swap(ret, heap[heapLen]);
heapLen--;
maxHeapify(1);
return ret;
}
三、算法分析:
查询操作 | O(1) |
堆维护操作 | O(logN) |
| 建堆操作 | O(NlogN) |
堆排序操作 | O(NlogN) |