数据范围 对于%100%的数据,n≤200000。
- 题目可以这样看:每个小朋友手上都有一个盒子,他们都有自己要传递的对象,当自己的盒子传到自己手中时,游戏结束。
- 把每个小朋友看做一个点,传递对象连起来之间的路径当做边,那么整到题就可以看作求最小环。
- 一些小朋友的盒子可能传到了一个环中出不来了,即环上的点的出边一定指向换上下一个点,其他点指向关系是一棵树,树根指向环上的点,这种图叫做基环内向树
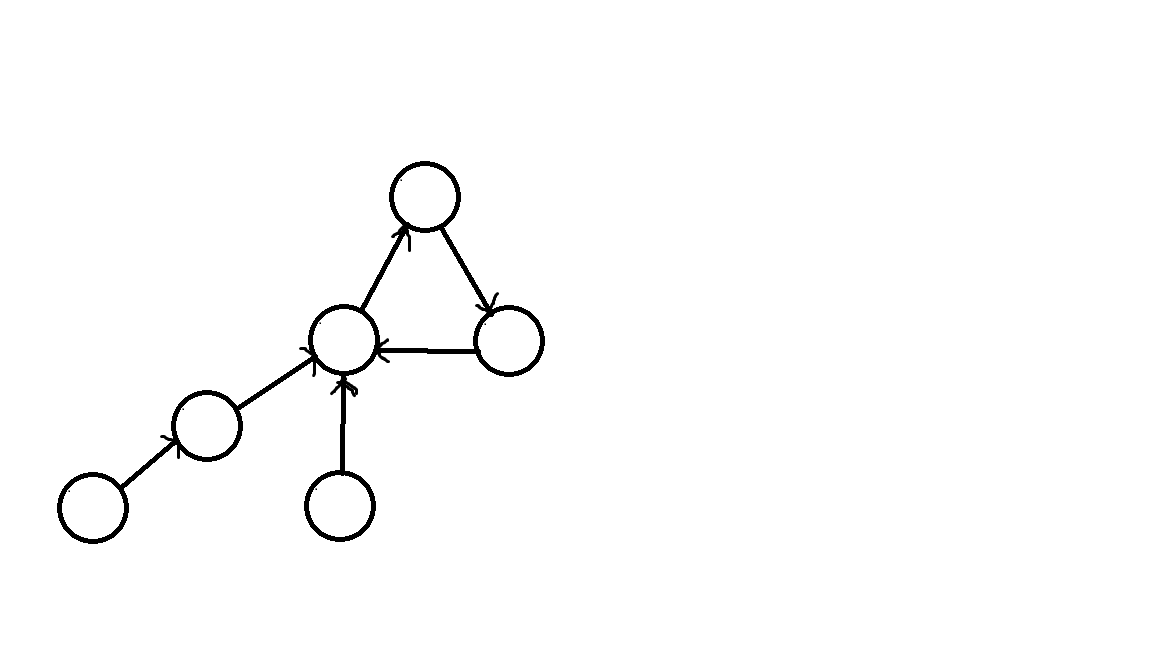
- 每个点只有一个出边
- 图中可能不止一个环
- 把树删掉,只留下环计算长度比较即可
删树部分
- 记录每个点的入度(有多少有向边连向自己)。
- 从入度为零的开始,对它通向的点的入度减一。
- 标记这个点。
- 如果通向的点的入度为零并且没有被标记,重复第二步。
扫一遍结束
- 标记指的是树的节点
- 删树结束后,剩下没被标记的点都是环上的点,可能有多个环,每个环过一遍即可,所以把过的点都标记,标记的一定是一个环上的点
- 枚举点,如果是环上的点,如果这个点所在的环没有过过,那么过一遍,与ans比较最小值。
一句话总结
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 200001;
int n,ans = 0x7fffffff;
int now,to[N];
int vis[N],rudu[N];
void del(int u){
rudu[to[u]]--;
vis[u] = 1;
if(!rudu[to[u]] && !vis[to[u]]) del(to[u]);
}
void dfs(int v, int cnt){
if(v == now) { ans = min(ans, cnt); return ; }
vis[v] = 1;
if(!vis[to[v]]) dfs(to[v], cnt + 1);
}
int main(){
cin >> n;
for(int i = 1; i <= n; ++i) cin >> to[i], rudu[to[i]]++;
for(int i = 1; i <= n; ++i) if(!rudu[i] && !vis[i]) del(i);
for(int i = 1; i <= n; ++i){
if(!vis[i]){
now = i;
dfs(to[i], 1);
}
}
cout << ans;
return 0;
}
