2015 Multi-University Training Contest 2

1001 Angry Trees

1002 Buildings

比赛的时候没看懂题。看完题解依旧WA好久。
偷看数据发现坑多。不容易考虑全。

假设m>=n，否则转置一下。
下面所描述的left，right，up，down全部和官方题解相同。

要注意。left，right与up，down在图上的取法是不一样的。

 

首先考虑无坏点的情况。取ans=n/2+1必然能覆盖整个图。此时全部纵向铺条。

如图所示为n=4，m=5的情况。

 

 

加上坏点后。要分两类讨论。

 

i) 当min（left，right）<=ans时。不妨设left<ans。

那么只要坏点左边（包含坏点）横向铺条。右边纵向铺条。一定能铺满。

如图所示为n=5，m=9，x=3，y=3的情况。

ii)当min(left,right)>ans时。我们需要进一步讨论 。

①如果坏点在x方向上处于中间位置（n为奇数时的x=n/2+1，n为偶数时的x=n/2或x=n/2+1）那么用长度为ans纵向铺条仍然可以。

如图分别为n=5，m=7，x=3，y=4与n=6，m=9，x=3，y=5的情况。

②如果x不在中间位置。 那么长度为ans的条已经无法覆盖全图了。(无论横铺还是纵铺。)

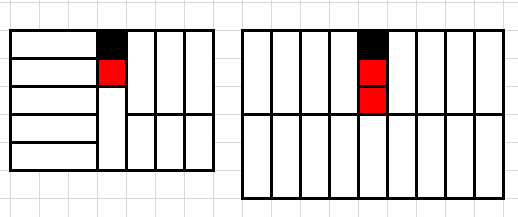
如图分别为n=5，m=7，x=1，y=4与n=6，m=9，x=1，y=5的情况。
红色表示无法覆盖的区域。

此时我们有两种方案（不妨设ans<left<=right）
1)在坏点左边（包含坏点）用 left长度横铺，右边（不包含坏点）纵铺。（因为left>ans。这是必然可行的。）
2)用max(up,down) 长度全部纵铺。
那么在1)与2)中选择更优的即为答案。

在n=5，m=7，x=1，y=4与n=6，m=9，x=1，y=5的情况下
方案1)与2)是相同的，两者均可。

如果考虑n=6，m=9，x=2，y=5的情况。那么显然方案2)更优。

最后一个坑。边长为奇数的方形且坏点在中间。答案为ans-1。

如图为n=5,m=5,x=3,y=3的情况。

# include <iostream>
# include <cstdio>
# include <algorithm>
using namespace std;

int main(void)
{
    int n,m,x,y;
    while((scanf("%d%d%d%d",&n,&m,&x,&y))!=EOF)
    {
        if(n>m) {swap(n,m); swap(x,y);}
        int ans=(n+1)/2;
        int left=y,right=m-y+1,up=x-1,down=n-x;
        if(min(left,right)>ans&&max(up,down)-min(up,down)>1)
            ans=min(min(left,right),max(up,down));
        if(n%2&&m==n&&left==right&&up==down) ans--;
        printf("%d
",ans);
    }
    return 0;
}

1003  Connect the Graph

1004 Delicious Apples

苹果数最多为1e5。所以把每个苹果看成一个点。

按中线将苹果分成左右两边。用dist表示每个苹果的距离。

cnt计两边苹果数。全部读好sort一遍。

先考虑贪心的取两边的苹果。

sum[i]表示在某一边取完1-i的苹果回去后走的最小路程。

递推sum数组直到sum[cnt]。

转移方程是i<=k时sum[i]=2*dist[i],i>k时sum[i]=sum[i-k]+2*dist[i]。

这样的话得到一个ans=suml[cntl]+sumr[cntr]。

然而会发现。如果贪心到最后在一边取的苹果不到k个。那么会存在走一圈更优的情况。

但是走一圈最多只有一次。因为如果多于一次就能拆成两个小于半圈的。必然小于一圈。

那么我们可以枚举走一圈的时候。分别在左半右半取了多少个。

例如左半取i个右半取k-i个。那么这i个一定要取左半距离最大的。右半同理。

这里要注意枚举时，枚举的个数不能超过左边和右边的总个数。

最后注意LL。

# include <iostream>
# include <cstdio>
# include <algorithm>
using namespace std;
typedef long long LL;
# define maxn 100010
int distl[maxn],distr[maxn];
LL suml[maxn]={0},sumr[maxn]={0};

int main(void)
{
    int T; cin>>T;
    while(T--)
    {
        LL L; int n,k;
        scanf("%I64d%d%d",&L,&n,&k);
        int cntl=0,cntr=0;
        for(int i=1;i<=n;i++)
        {
            int x,a; scanf("%d%d",&x,&a);
            for(int j=0;j<a;j++)
            {
                if(2*x<L) distl[++cntl]=x;
                else distr[++cntr]=L-x;
            }
        }
        sort(distl+1,distl+1+cntl);
        sort(distr+1,distr+1+cntr);
        for(int i=1;i<=cntl;i++)
        {
            if(i<=k) suml[i]=2*distl[i];
            else suml[i]=suml[i-k]+2*distl[i];
        }
        for(int i=1;i<=cntr;i++)
        {
            if(i<=k) sumr[i]=2*distr[i];
            else sumr[i]=sumr[i-k]+2*distr[i];
        }
        LL ans=suml[cntl]+sumr[cntr];
        for(int i=0;i<=k;i++)
        {
            int posl=max(0,cntl-(k-i));
            int posr=max(0,cntr-i);
            ans=min(ans,L+suml[posl]+sumr[posr]);
        }
        printf("%I64d
",ans);
    }
    return 0;
}

1005 Eastest Magical Day Seep Group's Summer

1006 Friends

连个暴搜都写不出来。不开心。

官方题解说搜点。加上两点优化：1.只考虑偶数边 2.最后一条边由前面的边确定。

在网上找到了简单易懂的做法。跑的不是很快是超级快。

先读边。每个点记下度数。如果有奇数的就直接输0过了。

所有点的度都是偶数的情况下。每个节点的on边与off边是相等的，即为度数一半。

直接搜边。枚举每条边分别是on边与off边的情况。

如果过程中有点的on边或者off边举完了。边还没搜完。

那么该情况就是不可行的。直接return。

# include <iostream>
# include <cstdio>
# include <cstring>
using namespace std;
# define CLR(x) memset(x,0,sizeof(x))
int ans,m,n,deg[10],on[10],off[10];

struct E
{
    int from,to;
} edge[30];

void dfs(int x)
{
    if(x>m) {ans++; return;}
    int u=edge[x].from,v=edge[x].to;
    if(on[u]&&on[v])
    {
        on[u]--; on[v]--;
        dfs(x+1);
        on[u]++; on[v]++;
    }
    if(off[u]&&off[v])
    {
        off[u]--; off[v]--;
        dfs(x+1);
        off[u]++; off[v]++;
    }
    return;
}

int main(void)
{
    int T; cin>>T;
    while(T--)
    {
        CLR(edge); CLR(deg); CLR(on); CLR(off);
        scanf("%d%d",&n,&m);
        for(int i=1;i<=m;i++)
        {
            int u,v; scanf("%d%d",&u,&v);
            edge[i].from=u; edge[i].to=v;
            deg[u]++; deg[v]++;
        }
        int ok=1;
        for(int i=1;i<=n;i++) if(deg[i]%2) {ok=0; break;}
        if(!ok) {printf("0
"); continue;}
        for(int i=1;i<=n;i++) on[i]=off[i]=deg[i]/2;
        ans=0; dfs(1);
        printf("%d
",ans);
    }
    return 0;
}

1007 Gorgeous Sequence

1008 He is Flying

1009 I Wanna Become A 24-Point Master

没什么技术含量。看官方题解。

只要能推出所有的情况就好。

然而把式子全部变成代码也挺不容易的。

一处WA整个都要重新检查一次。过的时候真的感动哭。

【第一次遇见说代码太长的情况。也有可能是HDU或者我网炸。】

# include <iostream>
# include <cstdio>
using namespace std;

int main(void)
{
    int n;
    while((scanf("%d",&n))!=EOF)
    {
        if(n<4) printf("-1
");
        if(n==4) printf("1 * 2
5 + 3
6 + 4
");
        if(n==5) printf("1 / 2
6 / 3
4 - 7
5 * 8
");
        if(n==6) printf("1 + 2
3 + 7
4 + 8
5 + 9
10 - 6
");
        if(n==7) printf("1 * 2
3 / 4
5 + 6
8 - 9
11 / 10
12 * 7
");
        if(n==8) 
        {
            printf("1 + 2
9 + 3
4 - 5
11 * 6
");
            printf("12 * 7
13 * 8
14 + 10
");
        }
        if(n==9)
        {
            printf("1 + 2
10 + 3
4 / 5
6 / 7
");
            printf("8 / 9
11 - 12
15 - 13
16 - 14
");
        }
        if(n==10)
        {
            printf("1 / 2
3 / 4
5 / 6
7 / 8
9 + 10
");
            printf("11 + 12
16 + 13
17 + 14
18 + 15
");
        }
        if(n==11)
        {
            printf("1 + 2
3 / 4
5 / 6
12 + 13
15 + 14
");
            printf("7 - 8
17 * 9
18 * 10
19 * 11
20 + 16
");
        }
        if(n==12)
        {
            printf("1 - 2
");
            for(int i=0;i<8;i++) printf("%d * %d
",i+3,i+13);
            printf("11 + 12
21 + 22
");
        }
        if(n==13)
        {
            printf("1 / 2
3 - 14
4 + 5
16 / 6
15 * 17
7 - 8
");
            for(int i=0;i<5;i++) printf("%d * %d
",i+9,i+19);
            printf("24 + 18
");
        }
        if(n==14)
        {
            printf("1 / 2
3 / 4
5 - 15
17 - 16
6 + 7
19 / 8
20 * 18
9 - 10
");
            for(int i=0;i<4;i++) printf("%d * %d
",i+11,i+22);
            printf("21 + 26
");
        }
        if(n>14)
        {
            printf("1 + 2
3 + 4
5 + 6
7 + 8
%d + 9
",n+1);
            for(int i=0;i<4;i++) printf("%d / %d
",n+2+i,i+10);
            printf("14 - 15
");
            for(int i=0;i<n-15;i++) printf("%d * %d
",i+16,n+10+i);
            printf("%d + %d
%d * %d
%d * %d
%d * %d
",2*n-5,n+6,2*n-4,n+7,2*n-3,n+8,2*n-2,n+9);
        }
    }
    return 0;
}

1010 JRY is Fighting