题目描述
输入格式
输出格式
样例
数据范围与提示
真的是个神题,学到了。读完题后很明显是树形概率dp,然而父亲儿子会相互影响,dp有后效性……然后我又想到了高斯消元,首先数据范围太大肯定不是正解,然后也不容易实现,就放弃了,打了个错解过了样例,拿了5分。(其实直接输出n可以拿10分的……)
【题解】
其实可以考虑把父亲对儿子和儿子对父亲分开考虑(T3也是两个数组dp的)。设f1[i]为i被自己或儿子点亮的概率。f2[i]为i被父亲点亮的概率;那么可以两边dfs分别求解两个数组。f1[叶子节点]=q[i];f1[i]=q[i]+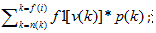
注:这里的加为概率加法,和容斥类似,P(a+b)=P(a)+P(b)-P(a)*P(b);对于i,若直接加,则多加了i即被自己点亮又被儿子点亮的情况。
f2[根节点]=f1[i];设pfa为父亲节点下传的概率,由于f2是有上向下更新,所以f2[fa]已知,pfa=f2[fa]-f1[v]*p()//解释:若fa已经点亮,则有两种情况1.fa被v点亮,2.fa不被v点亮。
所以用fa亮的概率减去fa被v点亮的概率就是fa下传的概率(这里是概率相减,P(A)=(P(A+B)-P(B))/(1-P(B)))。f2[v]=f1[v]+pfa*p();这里也是概率加法,排除v既是自己亮又被fa点亮的情
况。
Ps.还有一种方法记录的是不被点亮的概率,避免了概率的加减(其实我觉得这个也挺好理解的)。
#include<iostream>
#include<cstdio>
#include<cmath>
#define esp (1e-13)
using namespace std;
struct edge
{
int u,v,next;double p;
#define u(x) ed[x].u
#define v(x) ed[x].v
#define n(x) ed[x].next
#define p(x) ed[x].p
}ed[1000010];
int first[500010],num_e;
#define f(x) first[x]
int n;
double q[500010];
double f1[500010],f2[500010];
void dfs1(int x,int ff)
{
if(!f(x)){f1[x]=q[x];return;}
f1[x]=q[x];
for(int i=f(x);i;i=n(i))
if(v(i)!=ff)
{
dfs1(v(i),x);
f1[x]=f1[x]+f1[v(i)]*p(i)-f1[x]*f1[v(i)]*p(i);//注
}
}
void dfs2(int x,int ff)
{
double pfa=0;
for(int i=f(x);i;i=n(i))
if(v(i)!=ff)
{
if(fabs((1.0-f1[v(i)]*p(i))<esp))f2[v(i)]=1.0;
else
{
pfa=(f2[x] - f1[v(i)]*p(i))/(1.0-f1[v(i)]*p(i));//注
f2[v(i)]=f1[v(i)]+p(i)*pfa-f1[v(i)]*pfa*p(i);//注
}
dfs2(v(i),x);
}
}
inline void add_e(int u,int v,double p);
signed main()
{
// freopen("in.txt","r",stdin);
cin>>n;
int ta,tb;double tp;
for(int i=1;i<n;i++)
{
scanf("%d%d",&ta,&tb);cin>>tp;tp/=100.0;
add_e(ta,tb,tp);
add_e(tb,ta,tp);
}
for(int i=1;i<=n;i++)
cin>>q[i],q[i]/=100;
dfs1(1,0);
f2[1]=f1[1];
dfs2(1,0);
double ans=0;
for(int i=1;i<=n;i++)
ans+=f2[i];
printf("%0.6lf",ans);
}
inline void add_e(int u,int v,double p)
{
++num_e;
u(num_e)=u;
v(num_e)=v;
p(num_e)=p;
n(num_e)=f(u);
f(u)=num_e;
}