推一下$C_{2n}^n-C_{2n}^{n-1}$这个公式。
当n=m时 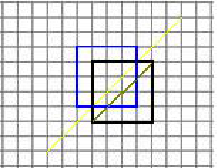 ,从黑格子左下角到右上角的方案数(不保证合法)为$C_{2n}^{n}$,相当于有2n个位置,其中选出n个向右,另外n个向上。
,从黑格子左下角到右上角的方案数(不保证合法)为$C_{2n}^{n}$,相当于有2n个位置,其中选出n个向右,另外n个向上。
然后看不合法的方案。不合法则肯定经过了黄线,从第一次到达黄线开始,以后的路径沿黄线反转,那么不合法的方案数就是从黑格子左下角到蓝格子右上角的方案数
$C_{2n}^{n-1}$,总方案数为$C_{2n}^n-C_{2n}^{n-1}$.
当n>m时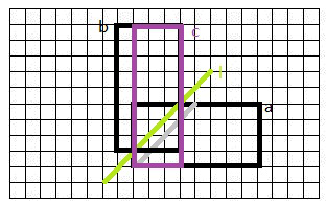
所以答案为C(n+m,n)-C(n+m,m-1) 再用一个高精度。

1 #include<algorithm> 2 #include<iostream> 3 #include<cstring> 4 #include<cstdio> 5 #define LL long long 6 //#define int LL 7 #define ma(x) memset(x,0,sizeof(x)) 8 using namespace std; 9 struct sz 10 { 11 int a[20000]; 12 }; 13 int n,m; 14 15 void print(sz &a) 16 { 17 for(int i=1;i<=a.a[0];i++)cout<<a.a[i]; 18 puts(""); 19 } 20 sz mul(sz &a,int b) 21 { 22 sz c;ma(c.a); 23 c.a[0]=a.a[0]; 24 for(int i=1;i<=a.a[0];i++) 25 c.a[i]=a.a[i]*b; 26 for(int i=1;i<=c.a[0];i++) 27 if(c.a[i]>=10) 28 { 29 c.a[i+1]+=c.a[i]/10; 30 c.a[i]%=10; 31 if(i==c.a[0])c.a[0]++; 32 } 33 return c; 34 } 35 sz div(sz &a,int b) 36 { 37 sz ans;ma(ans.a); 38 int yu=0; 39 for(int i=1;i<=a.a[0];i++) 40 { 41 yu=yu*10+a.a[i]; 42 if(yu/b>0) 43 { 44 ans.a[++ans.a[0]]=yu/b; 45 yu%=b; 46 } 47 else if(ans.a[0])ans.a[0]++; 48 } 49 return ans; 50 } 51 signed main() 52 { 53 cin>>n>>m; 54 sz a;a.a[0]=a.a[1]=1; 55 for(int i=n+2;i<=n+m;i++)a=mul(a,i); 56 a=mul(a,n+1-m); 57 reverse(a.a+1,a.a+1+a.a[0]); 58 for(int i=2;i<=m;i++)a=div(a,i); 59 print(a); 60 }
