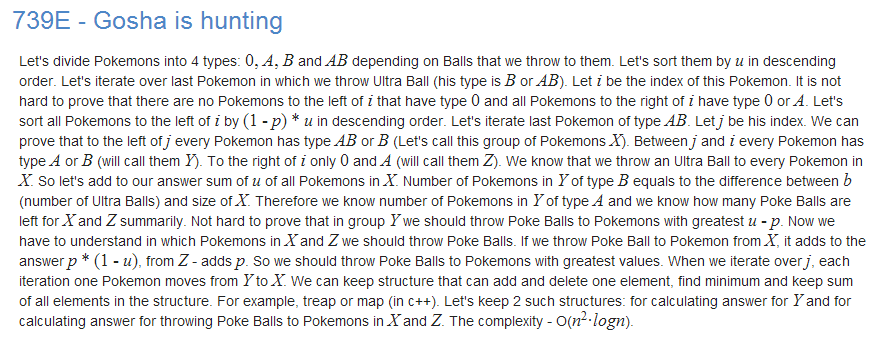本来没有打算写题解的,时间有点紧。但是这个wqs二分看了好久才明白还是写点东西吧。
题解就直接粘dg的了:
赤(red)
本题来自codeforces 739E,加大了数据范围.
首先对一只猫不会扔两个及以上数量的同种食物。最优方案一定把食物用完.
每只猫对期望的贡献可以根据期望的线性性分开算的,不投喂,则这只猫贡献为0;
只喂干脆面,贡献为pi;只喂豆干,贡献为qi;两种都喂,贡献为pi+qi-pi*qi
算法1:
对于每只猫,只有4种情况,所以我们大力枚举一下,单组数据O(4^n),可以通过第1个测试点,期望得分10分。
算法2:
对于第2个测试点,有刚好等于猫数的豆干或干脆面,那么我们把等于猫数的食品一只猫喂一个,考虑每只猫多喂另一种食品后能新得到的贡献,例如,第i只猫已经喂了一个豆干,再喂一包干脆面对期望的贡献为(1-qi)*pi,可以认为不喜欢豆干时干脆面才会新产生贡献。我们排个序就好了,单组数据O(n+nlogn),结合算法1,期望得分20分.
算法3:
考虑DP,定义f[i][j][k]为前i只猫投喂j包干脆面和k包豆干时得到的最大期望猫数,转移时考虑第i只猫如何投喂,复杂度O(nab),可以通过1,2,3,4号测试点,期望得分40分。
算法4:
注意到第5个测试点的a和b都相当大,那么没有被投喂的猫就会相对较少,我们考虑对没有被投喂的猫进行DP。不妨先给所有的猫都同时投喂两种食品,然后再收回n-a包豆干和n-b包干脆面,最小化期望猫数的损失即可。DP和算法3类似,时间复杂度O(n(n-a)(n-b))结合算法3,期望得分50分。
第6到7个测试点是为复杂度较优的算法准备的。
算法5:
考虑网络流。给一只猫分配一包干脆面可以得到pi的收益,给一只猫分配一包豆干可以得到qi的收益,但同时分配这两种食品将损失pi*qi的收益.如果不考虑pi*qi的损失,有一个很明显的费用流建图:建两个点表示豆干和干脆面,从原点向这两个点分别连费用为0,流量等于对应食品数目的边,从干脆面向每只猫连流量为1,费用为pi的边,从豆干向每只猫连流量为1,费用为qi的边,从每只猫向汇点连流量为2,费用为0的边。那么pi*qi的损失应当可以加到这个比较简单的模型的某一条边上。聪明的你一定想到了,我们把从猫连向汇点的边拆成两条,流量均为1,但一条费用为0,一条费用为-pi*qi,这样跑出来就是对的。
时间复杂度O(费用流).
期望得分70分
算法6:
cf官方题解的方法,用数据结构维护贪心。可见这个题并没有考网络流
期望得分70分
算法7
这是一种被称作Wqs二分(wqs=王钦石)的黑科技。熟悉wqs二分的选手可以直接去看算法8了.
假设看这里的选手没有听说过wqs二分.
考虑如何优化算法3的O(n^3)DP.
我们首先不考虑b的限制,假设豆干可以任意使用,定义f[i][j]表示前i只猫使用j包干脆面和若干包豆干得到的最大收益。直接这么DP会n只猫都用豆干,可能会超出b的限制。
为了减少豆干的使用,我们可以假定使用一个豆干需要额外付出cost的代价(也就是在转移的时候如果一只猫用了豆干,它对期望值的贡献要减去cost).在DP的时候,求解出f[i][j]的最大值,并记录最优方案中豆干使用的数目x,那么此时真实的期望是f[i][j]的最优值加上x*cost,这个结果必然也是用了x个 豆干时能够得到的最优结果.
但是,如果我们随便假定一个cost去跑DP,得到的方案并不一定把所有豆干都用完,我们需要一个能把所有豆干都用完的cost的值.
显然豆干使用量随着cost的变化是单调变化的,我们可以二分cost的数值.
时间复杂度O(n2logn)
期望得分70分.
算法8(满分算法)
我们还可以做到O(nlog2n),具体做法在算法7的基础上,wqs二分套wqs二分,把DP再减少一维。假设用豆干有cost1的额外花费,用干脆面有cost2的额外花费.f[i]表示前i只猫的最大收益.然后外层二分cost1内层二分cost2.
看标程理解一下吧.
这个做法当然不是lrd想出来的啦.
出处:http://codeforces.com/blog/entry/49691
出题人的预测:NOIP水平的选手拿到本题的前50分就不错了.这50分应当还是有区分度的.水平稍高的选手可能打出一种复杂度较好的算法拿到70分.满分做法应当是相当难想到的.

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<cmath> 5 #define int long long 6 #define MP(a,b) make_pair(a,b) 7 using namespace std; 8 const double esp=1e-10; 9 int n,a,b; 10 double p[100010],q[100010]; 11 struct zt 12 { 13 int x,y;double val; 14 void clear(){x=val=y=0;} 15 friend bool operator < (zt a,zt b) 16 { 17 if(a.val!=b.val)return a.val<b.val; 18 if(a.y!=b.y)return a.y>b.y; 19 return a.x>b.x; 20 } 21 }f[2]; 22 inline int read(); 23 signed main()//清空 24 { 25 while(cin>>n>>a>>b) 26 { 27 for(int i=1;i<=n;i++)scanf("%lf",&p[i]); 28 for(int i=1;i<=n;i++)scanf("%lf",&q[i]); 29 30 double L=0,R=1,cost1,ans=0,cost2; 31 while(R-L>=esp) 32 { 33 cost1=(L+R)/2;f[0].clear(),f[1].clear(); 34 double l=0,r=1;zt res;res.clear(); 35 while(r-l>=esp) 36 { 37 cost2=(l+r)/2;f[0].clear();f[1].clear(); 38 for(int i=1;i<=n;i++) 39 { 40 int now=i%2,pre=(i-1)%2; 41 f[now]=f[pre];double tv; 42 tv=f[pre].val+p[i]-cost1; 43 if(tv-f[now].val>=esp)f[now]=(zt){f[pre].x+1,f[pre].y,tv}; 44 tv=f[pre].val+q[i]-cost2; 45 if(tv-f[now].val>=esp)f[now]=(zt){f[pre].x,f[pre].y+1,tv}; 46 tv=f[pre].val+p[i]+q[i]-p[i]*q[i]-cost1-cost2; 47 if(tv-f[now].val>=esp)f[now]=(zt){f[pre].x+1,f[pre].y+1,tv}; 48 } 49 int now=n%2; 50 if(f[now].y<=b)res=max(res,f[now]),r=cost2; 51 else l=cost2; 52 if(f[now].y==b){res=f[now];break;} 53 } 54 if(res.x<=a)ans=max(ans,res.val+res.x*cost1+res.y*cost2),R=cost1; 55 else L=cost1; 56 if(res.x==a)break; 57 } 58 printf("%0.5lf ",f[n%2].val+a*cost1+b*cost2); 59 // printf("%0.5lf ",ans); 60 } 61 } 62 inline int read() 63 { 64 int s=0,f=1;char a=getchar(); 65 while(a<'0'||a>'9'){if(a=='-')f=-1;a=getchar();} 66 while(a>='0'&&a<='9'){s=s*10+a-'0';a=getchar();} 67 return s*f; 68 }
dg的题解是真的详细,照着打应该不是很难。
但是关于wqs二分有一个细节好久才弄明白。
就是最后答案为什么是‘f[n%2].val+a*cost1+b*cost2’而不是‘f[n%2].val+f[n%2].x*cost1+f[n%2].y*cost2',明明只用了x包干脆面和y个豆干为什么要加上a,b的补充权值?
于是我在代码后面加了这个:‘if(f[n%2].x!=a||f[n%2].y!=b)puts("!!!!!!!!!!!1");’
最后求出来的x,y和a,b并不一样。但是显然都用完是最优的。问题在于可能并不存在一组cost1,cost2使得dp出来正好是都用完的,比如 所有的猫的p都相等而a<n,那么二分出来x要么是0要么是n。这种时候继续二分找到一个最贴近的补充权值cost1使得a*cost1最优。
大概就这些吧。