CF993E Nikita and Order Statistics 多项式卷积 快速傅里叶变换

题意：

　　给你一个数组a1~an，对于k=0~n，求出有多少个数组上的区间满足：区间内恰好有k个数比x小。x为一个给定的数。n<=10^5。值域没有意义。

 

分析：

　　大神们都说这道题是一个套路题，真是长见识%%%。

　　首先我们可以将题面转化，因为x是预先给出的，所以我们可以对其进行预处理，将数列中小于x的数都设为1，其他都为0，然后求一个前缀和，另前缀和数组为s[i]我们开一个数组v[i]，记录在前缀和数组中数值i出现的次数。

　　然后我们可以得到这样一个式子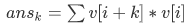

　　（据说看到这个式子就是套路了）

　　然后我们对这个式子进行一个转化。

　　转化：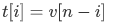

　　之后，我们就可以修改上面的式子，变成这样，

　　有些经验的选手可以看得出，这个形式就是一个卷积的形式。

　　所以我们就直接把v数组和t数组看成多项式，用fft做一遍卷积，之后n+k次项的系数就是ans_k

　　k=0时需要特殊处理一下，要去除空串的影响，并且当k=0是，由于i和j的顺序问题，所以每种情况都统计了两次，最后要除以2。

代码：

#include<bits/stdc++.h>
#include<complex>
#define db double
#define ll long long
#define cp complex<db>
using namespace std;
const int N=1000005;
const db pi=acos(-1);
int m,l,r[N],cnt[N],s[N],x;
cp a[N],b[N],omg[N],inv[N];ll n,ans[N];
void init(){
    for(int i=0;i<n;i++)
    omg[i]=cp(cos(2*pi*i/n),sin(2*pi*i/n)),
    inv[i]=conj(omg[i]);
} void fft(cp *a,cp *tmp){
    int lm=0;while((1<<lm)<n) lm++;
    for(int i=0;i<n;i++){int t=0;
        for(int j=0;j<lm;j++)
        if((i>>j)&1) t|=(1<<(lm-j-1));
        if(i<t) swap(a[i],a[t]); 
    } for(int l=2;l<=n;l*=2){
        int m=l/2;
        for(cp *p=a;p!=a+n;p+=l)
        for(int i=0;i<m;i++){
            cp t=tmp[n/l*i]*p[i+m];
            p[i+m]=p[i]-t;p[i]+=t;
        }
    } return ;
} int main(){
    scanf("%lld%d",&n,&x);cnt[0]=1;
    for(int i=1,y;i<=n;i++)
    scanf("%d",&y),s[i]=s[i-1]+(y<x),cnt[s[i]]++;
    for(int i=0;i<=n;i++) a[i]=b[n-i]=cnt[i];
    int q=n;n=1;while(n<=(q<<1)) n<<=1;
    init();fft(a,omg);fft(b,omg);
    for(int i=0;i<n;i++) a[i]*=b[i];
    fft(a,inv);
    ans[0]=(ll)((a[q].real()/n+0.5)-1ll*q-1)>>1ll;
    printf("%lld",ans[0]);
    for(int i=1;i<=q;i++)
    ans[i]=(ll)floor(a[q+i].real()/n+0.5),
    printf(" %lld",ans[i]);puts("");return 0;
}