看到这道题,网上没有中文版的官方题解,于是就自己翻译了一遍。
不是机器翻译,是一个字一个字纯手翻译的,如果有错误欢迎指正。
比如我们有一张卡片,三个参数分别是 a1 = 4, b1 = 2, c1 = 3. 方便起见,我们令 p = q = r = 5.
考虑什么样的卡片能够击败这张. 我们可以固定一个参数c,来观察对于不同的c,有什么特殊的性质:

注意在第c个坐标系中,坐标为(a,b)的绿色方格代表一张卡片 (a, b, c) 可以击败我们这张卡片 (4, 2, 3). 因此,对于所有c个坐标系中的绿色方格总数就是能击败这张卡片卡片总数。这种表示方法很重要, 因为我们可以简单地考虑更多的卡片.比如我们有这样一张卡片 a2 = 2, b2 = 3, c2 = 4:
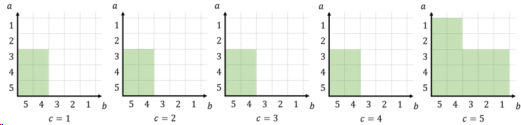
现在,考虑我们想同时击败这两张卡片时是什么情况?显然,我们只需要把对应的两个坐标系求交集即可。
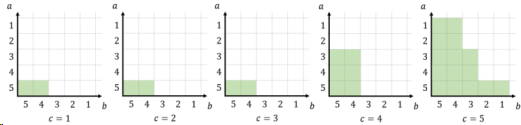
记住,我们只需要算得每个坐标系中的绿色方格数量。
事实证明,我们很难直接计算出绿色方格的数量。相反,计算非绿色的方格数量是更加可行的,这时我们只需要将其从所有pqr坐标系中减去即可。
怎么做?我们要利用这些网格的一些优美的性质。
首先,对于每个特定的卡片(ai, bi, ci),所有的 1 到 ci 坐标系是相同的, 并且所有的 ci + 1 到 r 的坐标系也是相同的。这就是说我们可以避免大量冗余计算,而且仅当状态变化时我们才需要进行更新。
其次,如果一个方格(a, b)对于一个固定的c不是绿色的, 那么对于相同的c,满足a' ≤ a, b' ≤ b的所有方格(a', b') 也不是绿色的。这就意味着我们可以用一个数组u1, u2, u3, ...代替c相同的坐标系,其中ua表示所有非绿的(a, b)中最大的b. 另外, u1 ≥ u2 ≥ u3 ≥ ... ≥ up.
再其次,对于每张卡片,每一个特定的c,u数组中最多只有两种不同的取值
最后,对于每张卡片,当c<c’时,c坐标系的u数组中任何一个值ui都不小于c’ 坐标系的u’数组中的对应取值u’i。
尽管这些性质都是显而易见容易证明的, 但会成为我们解决问题的良方。
我们从c = r 到 c = 1枚举c. 假设我们维护一个初始全零的数组s. 将用来保存对于每个c的非绿方格总数。
我们首先对于每个坐标系进行更新. 对于每张卡片, 每个i,将si 取max(si, ui)。
当然,对于每个坐标系求出答案需要O(np)的时间复杂度, 这太慢了。 解决这个问题,我们可以把s数组建成线段树。现在,对于每一个卡片i,我们只需要将s1, s2, s3, ..., sai 设置为max(sj, bi) 。
因为s数组实际上是一组u的最大值,这些是不被其他性质所增加的,所以s数组一直是不增加的。所以这些更新很容易做; 我们把sk, sk + 1, sk + 2, ..., sai 设置为bi,k是最小的满足bi ≥ sk的数。我们可以二分找到k, 线段树上二分可以做到O(log p)的复杂度。O(log^2 p)的复杂度可能通过这道题有些困难。
执行上述操作,我们就能在O(nlog p)的时间复杂度之内生成c=r时的相应s数组。使用线段树我们就能够随时统计s数组总和,这就能允许我们统计所有非绿色格子的数量。
现在我们将从c=r向c=1枚举c,并观察那个网格发生了变化(开始的时候对卡片按照c参数排序,之后双指针扫描就可以了) 所有坐标系网格都可以按照之前的方法更新。当坐标系发生变化时,好在我们有第四条性质,保证ui不会减少,只会变得更大。所以,我们只能更新两个范围:将s1, s2, s3, ..., sai 更新为 r 以及sai + 1, sa2 + 1, sai + 3, ..., sp 更新为 max(sj, bi). 前者更新颇为简单, 后者就需要像之前一样用二分查找完成.
当我们更新完每一个特定的c表示的坐标系时,得到了这个范围的权值和,然后再倒着枚举c,这样直到我们枚举到1。我们将在每个c坐标系中找到非绿色方格的总数,从中我们就可以得出绿色的方格总数,这样就可以得到答案。
对卡片排序花费 O(nlogn)的时间复杂度, 建出线段树s花费O(p) 的时间复杂度,并且有O(n)个更新操作每个花费O(log p)的时间复杂度,枚举花费O(r)的时间复杂度。因此最终的运行时间复杂度是O(n(log n + log p)+p+r) ,这样的复杂度足以通过此题。
题解也可以修改一下可以通过 p, q, r ≤ 10^9的数据;可是,并没有出现这样的要求,因为思想都是一样的,只不过增加了不少编程复杂度,如果有意,可以自行实现一下。