用python编写排序算法

交换排序 ＝＝＝ 冒泡排序，快速排序

插入排序 ＝＝＝直接插入排序，希尔排序

选择排序 ＝＝＝ 简单选择排序，堆排序

归并排序

基数排序

冒泡排序

要点

冒泡排序是一种交换排序。

什么是交换排序呢？

交换排序：两两比较待排序的关键字，并交换不满足次序要求的那对数，直到整个表都满足次序要求为止。

原理：比较两个相邻的元素，将值大的元素交换到前面。

算法思想

它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。

这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端，故命名冒泡。

假设有一个大小为 N 的无序序列。冒泡排序就是要每趟排序过程中通过两两比较，找到第 i 个小（大）的元素，将其往上排。

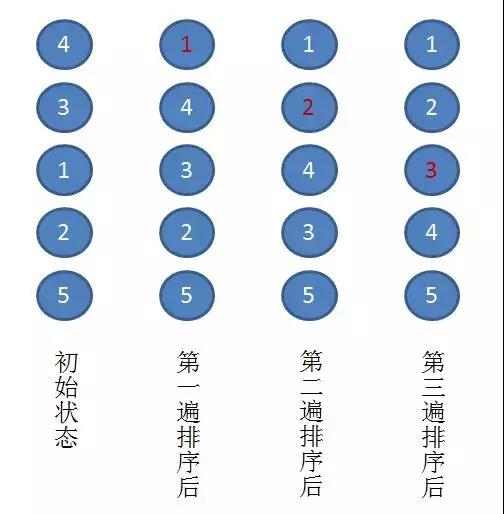
以上图为例，演示一下冒泡排序的实际流程：

假设有一个无序序列 { 4. 3. 1. 2, 5 }

• 第一趟排序：通过两两比较，找到第一小的数值 1 ，将其放在序列的第一位。

• 第二趟排序：通过两两比较，找到第二小的数值 2 ，将其放在序列的第二位。

• 第三趟排序：通过两两比较，找到第三小的数值 3 ，将其放在序列的第三位。

至此，所有元素已经有序，排序结束。

要将以上流程转化为代码，我们需要像机器一样去思考，不然编译器可看不懂。

假设要对一个大小为 N 的无序序列进行升序排序（即从小到大）。

• 每趟排序过程中需要通过比较找到第 i 个小的元素。

• 所以，我们需要一个外部循环，从数组首端(下标 0) 开始，一直扫描到倒数第二个元素（即下标 N - 2) ，剩下最后一个元素，必然为最大。

假设是第 i 趟排序，可知，前 i-1 个元素已经有序。现在要找第 i 个元素，只需从数组末端开始，扫描到第 i 个元素，将它们两两比较即可。

• 所以，需要一个内部循环，从数组末端开始（下标 N - 1），扫描到 (下标 i + 1)。

def bubbleSort(list):
    # 外层循环
    for j in range(len(list) - 1):
        count = 0
        # 内层循环
        for i in range(0, len(list)-1-j):
            if list[i] > list[i + 1]:
                list[i], list[i + 1] = list[i + 1], list[i]
                count += 1
        if 0 == count:
            break


if __name__ == '__main__':
    list = [32, 12, 66, 17, 80, 58, 46, 25, 74]
    print(list)
    bubbleSort(list)
    print(list)

算法分析

冒泡排序算法的性能

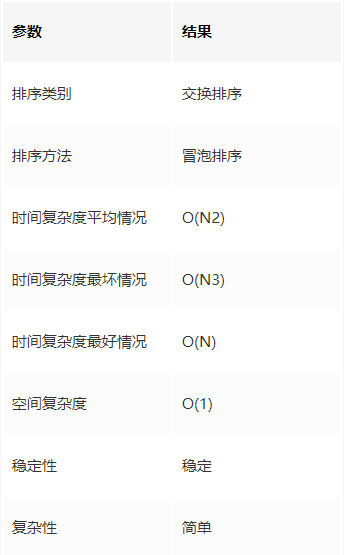
时间复杂度

由上面的例子可知  总的遍历比较次数为 4 + 3 + 2 + 1 = 10次

对于n位的数列则有比较次数为 (n-1) + (n-2) + ... + 1 = n * (n - 1) / 2，这就得到了最大的比较次数
而O(N^2)表示的是复杂度的数量级。举个例子来说，如果n = 10000，那么 n(n-1)/2 = (n^2 - n) / 2 = (100000000 - 10000) / 2，相对10^8来说，10000小的可以忽略不计了，所以总计算次数约为0.5 * N^2。用O(N^2)就表示了其数量级（忽略前面系数0.5）。

若文件的初始状态是正序的，一趟扫描即可完成排序。所需的关键字比较次数 C 和记录移动次数 M 均达到最小值：Cmin = N - 1, Mmin = 0。所以，冒泡排序最好时间复杂度为 O(N)。

若初始文件是反序的，需要进行 N -1 趟排序。每趟排序要进行 N - i 次关键字的比较(1 ≤ i ≤ N - 1)，且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下，比较和移动次数均达到最大值：

Cmax = N(N-1)/2 = O(N2)
Mmax = 3N(N-1)/2 = O(N2)

冒泡排序的最坏时间复杂度为 O(N2)。因此，冒泡排序的平均时间复杂度为 O(N2)。

总结起来，其实就是一句话：当数据越接近正序时，冒泡排序性能越好。

算法稳定性

冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较，交换也发生在这两个元素之间。

所以相同元素的前后顺序并没有改变，所以冒泡排序是一种稳定排序算法。

优化

对冒泡排序常见的改进方法是加入标志性变量swapped ，用于标志某一趟排序过程中是否有数据交换。

如果进行某一趟排序时并没有进行数据交换，则说明所有数据已经有序，可立即结束排序，避免不必要的比较过程。

def bubbleSort2(alist):
    list_len = len(alist)
    for i in range(list_len):
        # 定义一个swapped
        # 如果有元素交换过就置为True
        # 如果没有元素交换过就退出循环

        swapped = False
        for j in range(list_len-1-i):
            if alist[j] > alist[j+1]:
                alist[j],alist[j+1] = alist[j+1],alist[j]
                swapped = True
        # 搅拌排序
        # 从后面往前面检索，如果前面比后面的大，就交换
        if swapped:
            swapped = False
            # 由于上面已经有一个元素在最后排好序了，所以这时要减2
            for j in range(list_len - 2 - i,0,-1):
                if alist[j] < alist[j - 1]:
                    alist[j], alist[j - 1] = alist[j - 1], alist[j]
                    swapped = True
        # 如果没有发生元素交换，就说明列表已经是有序的了
        # 这时可以直接退出循环
        if not swapped:
            return alist


def main():
    print(bubbleSort2([22, 3, 1, 6, 7, 8, 2, 5]))

if __name__ == '__main__':
    main()

快速排序

要点

快速排序是一种交换排序。

快速排序由 C. A. R. Hoare 在 1962 年提出。

算法思想

它的基本思想是：

通过一趟排序将要排序的数据分割成独立的两部分：分割点左边都是比它小的数，右边都是比它大的数。

然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。方式不唯一

详细的图解往往比大堆的文字更有说明力，所以直接上图：

上图中，演示了快速排序的处理过程：

1. 初始状态为一组无序的数组：2、4、5、1、3。

2. 经过以上操作步骤后，完成了第一次的排序，得到新的数组：1、2、5、4、3。

3. 新的数组中，以 2 为分割点，左边都是比 2 小的数，右边都是比 2 大的数。

4. 因为 2 已经在数组中找到了合适的位置，所以不用再动。

5. 2 左边的数组只有一个元素 1，所以显然不用再排序，位置也被确定。（注：这种情况时，left 指针和 right 指针显然是重合的。因此在代码中，我们可以通过设置判定条件遍历 left 必须小于 right，如果不满足，则不用排序了）。

6. 而对于 2 右边的数组 5、4、3，设置 left 指向 5，right 指向 3，开始继续重复图中的一、二、三、四步骤，对新的数组进行排序。

分解和合并迭代实现方式：

在数列之中，选择一个元素作为"基准"（pivot），或者叫比较值。

数列中所有元素都和这个基准值进行比较，如果比基准值小就移到基准值的左边，如果比基准值大就移到基准值的右边

以基准值左右两边的子列作为新数列，不断重复第一步和第二步，直到所有子集只剩下一个元素为止。

quick_sort = lambda array: array if len(array) <= 1 else quick_sort([item for item in array[1:] if item <= array[0]]) + [array[0]] + quick_sort([item for item in array[1:] if item > array[0]])

　简洁快排匿名函数生成器

代码实现：

def quick_sort(arr):
    """快速排序"""
    if len(arr) < 2:
        return arr
    # 选取基准，随便选哪个都可以，选中间的便于理解
    base = arr[len(arr) // 2]
    # 定义基准值左右两个空数列用于存放排序后的
    left, right = [], []
    # 从原始数组中移除基准值
    arr.remove(base)
    for i in arr:
        # 大于基准值放右边
        if i >= base:
            right.append(i)
        else:
            # 小于基准值放左边
            left.append(i)
    # 使用迭代进行比较
    return quick_sort(left) + [base] + quick_sort(right)

算法分析

快速排序算法的性能

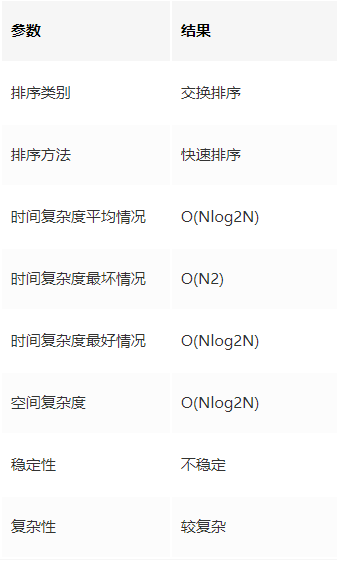
时间复杂度

当数据有序时，以第一个关键字为基准分为两个子序列，前一个子序列为空，此时执行效率最差。

而当数据随机分布时，以第一个关键字为基准分为两个子序列，两个子序列的元素个数接近相等，此时执行效率最好。

所以，数据越随机分布时，快速排序性能越好；数据越接近有序，快速排序性能越差。

空间复杂度

快速排序在每次分割的过程中，需要 1 个空间存储基准值。而快速排序的大概需要 Nlog2N 次的分割处理，所以占用空间也是 Nlog2N 个。

算法稳定性

在快速排序中，相等元素可能会因为分区而交换顺序，所以它是不稳定的算法。

快速排序优化

分治思想的排序在处理大数据集量时效果比较好，小数据集性能差些。

快速排序有一个缺点就是对于小规模的数据集性能不是很好。可能有人认为可以忽略这个缺点不计，因为大多数排序都只要考虑大规模的适应性就行了。但是快速排序算法使用了分治技术，最终来说大的数据集都要分为小的数据集来进行处理，所以快排分解到最后几层性能不是很好，所以我们就可以使用扬长避短的策略去优化快排：

1. 先使用快排对数据集进行排序，此时的数据集已经达到了基本有序的状态
2. 然后当分区的规模达到一定小时，便停止快速排序算法，而是改用插入排序，插入排序在对基本有序的数据集排序有着接近线性的复杂度，性能比较好。

 

插入排序

要点

直接插入排序是一种最简单的插入排序。

插入排序：每一趟将一个待排序的记录，按照其关键字的大小插入到有序队列的合适位置里，直到全部插入完成。

算法思想

在讲解直接插入排序之前，先让我们脑补一下我们打牌的过程。

• 先拿一张 5 在手里，

• 再摸到一张 4，比 5 小，插到 5 前面，

• 摸到一张 6，嗯，比 5 大，插到 5 后面，

• 摸到一张 8，比 6 大，插到 6 后面，

• 。。。

• 最后一看，我靠，凑到的居然是同花顺，这下牛逼大了。

以上的过程，其实就是典型的直接插入排序，每次将一个新数据插入到有序队列中的合适位置里。

很简单吧，接下来，我们要将这个算法转化为编程语言。

假设有一组无序序列 R0, R1, … , RN-1。

• 我们先将这个序列中下标为 0 的元素视为元素个数为 1 的有序序列。

• 然后，我们要依次把 R1, R2, … , RN-1 插入到这个有序序列中。所以，我们需要一个外部循环，从下标 1 扫描到 N-1 。

• 接下来描述插入过程。假设这是要将 Ri 插入到前面有序的序列中。由前面所述，我们可知，插入 Ri 时，前 i-1 个数肯定已经是有序了。

所以我们需要将 Ri 和 R0 ~ Ri-1 进行比较，确定要插入的合适位置。这就需要一个内部循环，我们一般是从后往前比较，即从下标 i-1 开始向 0 进行扫描。

核心代码

def insertionSort(arr): 
  
    for i in range(1, len(arr)): 
  
        key = arr[i] 
  
        j = i-1
        while j >=0 and key < arr[j] : 
                arr[j+1] = arr[j] 
                j -= 1
        arr[j+1] = key 
  
  
arr = [12, 11, 13, 5, 6] 
insertionSort(arr) 
print ("排序后的数组:") 
for i in range(len(arr)): 
    print ("%d" %arr[i])

------------------------

arr = [1,12,2, 11, 13, 5, 6,18,4,9,-5,3,11] 
def insertionSort(arr):
    #从要排序的列表第二个元素开始比较
    for i in range(1,len(arr)):
        j = i
        #从大到小比较，直到比较到第一个元素
        while j > 0:
            if arr[j] < arr[j-1]:
                arr[j-1],arr[j] = arr[j],arr[j-1]
            j -= 1        
    return arr
print(insertionSort(arr))

----------------------------------

# 一次往数组添加多个数字
def AppendNumbers(array):
    num = input('Numbers:(split by spaces)	').split()
    for i in num:
        array.append(int(i))
    print('排序前数组：{}.'.format(array))

def InsertionSort(array):
    AppendNumbers(array)  # 添加

    list = []
    while True:
        for i in array:
            minimum = min(array)
            if i == minimum:
                list.append(i)
                array.remove(i)  # 删去最小值

        if array == []:
            break

    print('排序后数组：{}.'.format(list))

array = [6, 4, 45, -2, -1, 2, 4, 0, 1, 2, 3, 4, 5, 6, -4, -6,  7, 8, 8, 34, 0]
InsertionSort(array)

算法分析

直接插入排序的算法性能

时间复杂度

当数据正序时，执行效率最好，每次插入都不用移动前面的元素，时间复杂度为 O(N)。

当数据反序时，执行效率最差，每次插入都要前面的元素后移，时间复杂度为 O(N2)。

所以，数据越接近正序，直接插入排序的算法性能越好。

空间复杂度

由直接插入排序算法可知，我们在排序过程中，需要一个临时变量存储交换的数据和下标，不需要额外的存储空间，所以空间复杂度为 1 。

算法稳定性

直接插入排序的过程中，不需要改变相等数值元素的位置，所以它是稳定的算法。

插入排序优化

当有序区间数据量很大时，查找数据的插入位置就会显得非常耗时，插入排序算法每次都是从有序区间查找插入位置，以此为切入点，我们可以使用二分查找法来快速确认待插入的位置，于是就有了优化版的插入排序算法，也叫二分查找插入算法。

def insert_sort(data_list):
    '''
    无优化版
    '''
    count=0 #统计循环次数
    length = len(data_list)
    for i in range(1,length ): #默认第一个位置的元素是已排序区间，因此下标从 1 开始
        tmp = data_list[i] #待插入的数据
        j = i 
        while j > 0: #从已排序区间查找插入位置
            count +=1
            if tmp < data_list[j-1]:
                data_list[j] = data_list[j-1]  #元素向后移动，腾出插入位置
            else:
                break
            j -= 1
        data_list[j] = tmp #插入操作
        print(data_list)
    print(f"总循环次数为 {count}")
    return data_list

if __name__ == "__main__":
    unsort = [1,3,4,2,1,5,6,7,8,4]
    print(*insert_sort(unsort)) 
------------------------------------------------------------
上述代码中的 count 只是为了统计循环次数，目的是和优化版的进行对比，当然您也可以对时间复杂度进行分析来对比性能的差异。 print(data_list) 是为了打印出每一次插入后数据列的结果，您可以对比结果来理解插入排序算法。

----------------------------------------------------------------
def insert_sort2(data_list):
    '''
    使用二分查找函数确定待插入元素在有序区间的插入位置
    '''
    count=0 #统计循环次数
    length = len(data_list)
    for i in range(1,length ): #默认第一个位置的元素是已排序区间，因此下标从 1 开始
        print(data_list)
        wait_insert_data = data_list[i] ##等待插入元素
        move_index = i 
        insert_index,count1 = binary_search(data_list[0:i],wait_insert_data) #寻找插入位置
        count+=count1 #统计循环次数需要加上二分查找的循环次数
        while move_index > insert_index: #移动元素，直到待插入位置处
            count+=1
            data_list[move_index] = data_list[move_index - 1]
            move_index -= 1
        data_list[insert_index] = wait_insert_data #插入操作
        print(data_list)
    print(f"总循环次数为 {count}")
    return data_list


def binary_search(data_list,data):    
    """
    输入:有序列表，和待查找的数据data
    输出：data 应该在该有序列表的插入位置
    count 变量纯粹是为了统计循环次数而使用的，实际应用时可去除。
    """
    count = 0
    length = len(data_list)
    low = 0
    high = length-1
    ##如果给定元素大于等于最后一个元素，则插入最后元素位置的后面
    ##如果小于第一个元素，则插入位置0 
    if data >= data_list [length -1]: return length,0
    elif data < data_list [0]: return 0,0
    insert_index = 0 
    while low < high-1:
        count +=1
        mid = (low + high)//2 #python中的除法结果默认为浮点数取整数部分时使用 //
        if data_list[mid] > data:
            high = mid
            insert_index = high
        else:
            low = mid
            insert_index = low+1  #如果值相同或者值大于mid的值，那么插入位置位于其后面
    return insert_index,count

if __name__ == "__main__":
    unsort = [1,3,4,2,1,5,6,7,8,4]
    print(*insert_sort2(unsort))

希尔排序-分治思想的插入排序

要点

希尔(Shell)排序又称为缩小增量排序，它是一种插入排序。它是直接插入排序算法的一种威力加强版。

该方法因 DL．Shell 于 1959 年提出而得名。

算法思想

希尔排序的基本思想是：

把记录按步长 gap 分组，对每组记录采用直接插入排序方法进行排序。

随着步长逐渐减小，所分成的组包含的记录越来越多，当步长的值减小到 1 时，整个数据合成为一组，构成一组有序记录，则完成排序。

我们来通过演示图，更深入的理解一下这个过程。

在上面这幅图中：

初始时，有一个大小为 10 的无序序列。

在第一趟排序中，我们不妨设 gap1 = N / 2 = 5，即相隔距离为 5 的元素组成一组，可以分为 5 组。

• 接下来，按照直接插入排序的方法对每个组进行排序。

在** 第二趟排序中**，我们把上次的 gap 缩小一半，即 gap2 = gap1 / 2 = 2 (取整数)。这样每相隔距离为 2 的元素组成一组，可以分为 2 组。

• 按照直接插入排序的方法对每个组进行排序。

在第三趟排序中，再次把 gap 缩小一半，即 gap3 = gap2 / 2 = 1。这样相隔距离为 1 的元素组成一组，即只有一组。

• 按照直接插入排序的方法对每个组进行排序。此时，排序已经结束。

需要注意一下的是，图中有两个相等数值的元素 5 和 5 。我们可以清楚的看到，在排序过程中，两个元素位置交换了。

所以，希尔排序是不稳定的算法。

核心代码

def shell_sort(data_list):
    '''
    思想：分治策略
   使用 for 循环
    '''
    length = len(data_list)
    space  = length//2
    while space > 0:
        for i in range(space,length ): #默认第一个位置的元素是已排序区间，因此下标从 1 开始
            tmp = data_list[i] #待插入的数据
            for j in range(i-space,-1,-space): #从已排序区间查找插入位置
                if tmp < data_list[j]:
                    data_list[j+space] = data_list[j]  #元素向后移动，腾出插入位置
                    i = j #最后的j即为插入的位置
                else:
                    break
            data_list[i] = tmp #插入操作
            print(data_list)
        space = space // 2
    return data_list

    unsort = [9,8,7,6,5,4,3,2,1]
    print(*shell_sort(unsort)) 

----------------------------

def shell_sort2(data_list):
    '''
    思想：分治策略
    使用 while 循环
    '''
    length = len(data_list)
    space  = length//2
    while space > 0:
        i = space
        while i < length: #默认第一个位置的元素是已排序区间，因此下标从 1 开始
            tmp = data_list[i] #待插入的数据
            j = i
            while j >= space and data_list[j - space] > tmp: #从已排序区间查找插入位置
                data_list[j] = data_list[j-space]  #元素向后移动，腾出插入位置                    
                j -= space
            data_list[j] = tmp #插入操作
            print(data_list)
            i +=1
        space = space // 2
    return data_list


    unsort = [9,8,7,6,5,4,3,2,1]
    print(*shell_sort2(unsort)) 

算法分析

希尔排序的算法性能

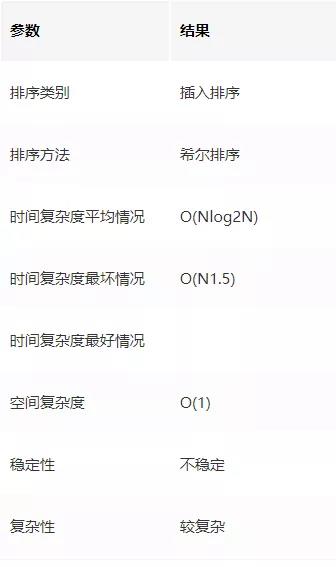
时间复杂度

步长的选择是希尔排序的重要部分。只要最终步长为 1 任何步长序列都可以工作。

算法最开始以一定的步长进行排序。然后会继续以一定步长进行排序，最终算法以步长为 1 进行排序。当步长为 1 时，算法变为插入排序，这就保证了数据一定会被排序。

Donald Shell 最初建议步长选择为 N/2 并且对步长取半直到步长达到 1。虽然这样取可以比 O(N2)类的算法（插入排序）更好，但这样仍然有减少平均时间和最差时间的余地。可能希尔排序最重要的地方在于当用较小步长排序后，以前用的较大步长仍然是有序的。

比如，如果一个数列以步长 5 进行了排序然后再以步长 3 进行排序，那么该数列不仅是以步长 3 有序，而且是以步长 5 有序。如果不是这样，那么算法在迭代过程中会打乱以前的顺序，那就不会以如此短的时间完成排序了。

已知的最好步长序列是由 Sedgewick 提出的(1, 5, 19, 41, 109,…)，该序列的项来自这两个算式。

这项研究也表明“比较在希尔排序中是最主要的操作，而不是交换。”用这样步长序列的希尔排序比插入排序和堆排序都要快，甚至在小数组中比快速排序还快，但是在涉及大量数据时希尔排序还是比快速排序慢。

算法稳定性

由上文的希尔排序算法演示图即可知，希尔排序中相等数据可能会交换位置，所以希尔排序是不稳定的算法。

直接插入排序和希尔排序的比较

• 直接插入排序是稳定的；而希尔排序是不稳定的。

• 直接插入排序更适合于原始记录基本有序的集合。

• 希尔排序的比较次数和移动次数都要比直接插入排序少，当 N 越大时，效果越明显。

• 在希尔排序中，增量序列 gap 的取法必须满足：**最后一个步长必须是 1 。**

• 直接插入排序也适用于链式存储结构；希尔排序不适用于链式结构。

def shell_sort(alist):
    n = len(alist)
    gap = n // 2
    while gap >= 1:
        for j in range(gap, n):
            i = j
            while i > 0:
                if alist[i] < alist[i-gap]:
                    alist[i], alist[i-1] = alist[i-1], alist[i]
                    i -= gap
                else:
                    break
        gap //= 2

    if __name__ == "__main__":
        li = [54,26,93,17,77,31,44,55,20]
        print(li)
        shell_sort(li)
        print(li)

简单选择排序

要点

简单选择排序是一种选择排序。

选择排序：每趟从待排序的记录中选出关键字最小的记录，顺序放在已排序的记录序列末尾，直到全部排序结束为止。

算法思想

• 从待排序序列中，找到关键字最小的元素；

• 如果最小元素不是待排序序列的第一个元素，将其和第一个元素互换；

• 从余下的 N - 1 个元素中，找出关键字最小的元素，重复 1、2 步，直到排序结束。

如图所示，每趟排序中，将当前**第 i 小的元素放在位置 i **上。

算法分析

简单选择排序算法的性能

时间复杂度

简单选择排序的比较次数与序列的初始排序无关。假设待排序的序列有 N 个元素，则**比较次数总是 N (N - 1) / 2 **。

而移动次数与序列的初始排序有关。当序列正序时，移动次数最少，为 0。

当序列反序时，移动次数最多，为 3N (N - 1) / 2。

所以，综合以上，简单排序的时间复杂度为 O(N2)。

空间复杂度

简单选择排序需要占用一个临时空间，在交换数值时使用。

示例代码

def SelectSort(input_list):
    l = len(input_list)
    if l == 0:
        return []
    sorted_list = input_list
    for i in range(l):
        #默认第i个元素是每次的最小值的索引
        min_index = i
        #找到后面元素最小的索引
        for j in range(i+1,l):
            if sorted_list[min_index] >sorted_list[j]:
                min_index = j
        #将找到的最小元素放入前面已经有序序列的末尾
        temp = sorted_list[i]
        sorted_list[i] = sorted_list[min_index]
        sorted_list[min_index] = temp
        print("%dth"%(i+1))
        print(sorted_list)
    return sorted_list
                
if __name__ == '__main__':
    input_list = [50,123,543,187,49,30,0,2,11,100]
    print("input_list:")
    print(input_list)
    sorted_list = SelectSort(input_list)
    print("sorted_list:")
    print(input_list)


input_list:
[50, 123, 543, 187, 49, 30, 0, 2, 11, 100]
1th
[0, 123, 543, 187, 49, 30, 50, 2, 11, 100]
2th
[0, 2, 543, 187, 49, 30, 50, 123, 11, 100]
3th
[0, 2, 11, 187, 49, 30, 50, 123, 543, 100]
4th
[0, 2, 11, 30, 49, 187, 50, 123, 543, 100]
5th
[0, 2, 11, 30, 49, 187, 50, 123, 543, 100]
6th
[0, 2, 11, 30, 49, 50, 187, 123, 543, 100]
7th
[0, 2, 11, 30, 49, 50, 100, 123, 543, 187]
8th
[0, 2, 11, 30, 49, 50, 100, 123, 543, 187]
9th
[0, 2, 11, 30, 49, 50, 100, 123, 187, 543]
10th
[0, 2, 11, 30, 49, 50, 100, 123, 187, 543]
sorted_list:
[0, 2, 11, 30, 49, 50, 100, 123, 187, 543]  

堆排序

要点

在介绍堆排序之前，首先需要说明一下，堆是个什么玩意儿。

堆是一棵顺序存储的完全二叉树。

其中每个结点的关键字都不大于其孩子结点的关键字，这样的堆称为小根堆。每个非叶子结点的值都要小于或者等于其左右孩子结点的值。

其中每个结点的关键字都不小于其孩子结点的关键字，这样的堆称为大根堆。每个非叶子结点的值都要大于或者等于其左右孩子结点的值。

举例来说，对于 n 个元素的序列 {R0, R1, … , Rn} 当且仅当满足下列关系之一时，称之为堆：

• Ri <= R2i+1 且 Ri <= R2i+2 （小根堆）

• Ri >= R2i+1 且 Ri >= R2i+2 （大根堆）

其中 i=1,2,…,n/2 向下取整;

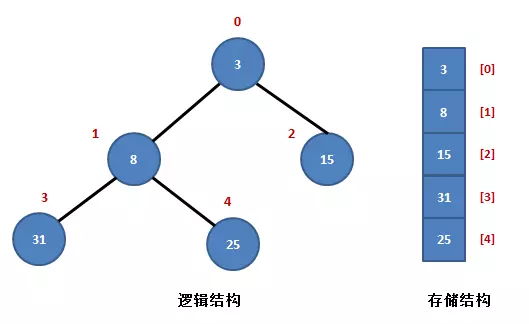
如上图所示，序列 R{3, 8,15, 31, 25} 是一个典型的小根堆。

堆中有两个父结点，元素 3 和元素 8。

元素 3 在数组中以 R[0] 表示，它的左孩子结点是 R[1]，右孩子结点是 R[2]。

元素 8 在数组中以 R[1] 表示，它的左孩子结点是 R[3]，右孩子结点是 R[4]，它的父结点是 R[0]。可以看出，它们满足以下规律：

设当前元素在数组中以 R[i] 表示，那么，

• 它的左孩子结点是：R[2*i+1];

• 它的右孩子结点是：R[2*i+2];

• 它的父结点是：R[(i-1)/2];

• R[i] <= R[2*i+1] 且 R[i] <= R[2i+2]。

算法思想

构建一个完全二叉树（序列 -> 完全二叉树 -> 大顶堆 -> 排序 - > 大顶堆 -> 排序 ...）

• 首先，按堆的定义将数组 R[0..n]调整为堆（这个过程称为创建初始堆），交换 R[0]和 R[n]；

• 然后，将 R[0..n-1]调整为堆，交换 R[0]和 R[n-1]；

• 如此反复，直到交换了 R[0]和 R[1]为止。

以上思想可归纳为两个操作：

• 根据初始数组去构造初始堆（构建一个完全二叉树，保证所有的父结点都比它的孩子结点数值大）。

• 每次交换第一个和最后一个元素，输出最后一个元素（最大值），然后把剩下元素重新调整为大根堆。

当输出完最后一个元素后，这个数组已经是按照从小到大的顺序排列了。

先通过详细的实例图来看一下，如何构建初始堆。

设有一个无序序列 { 1, 3,4, 5, 2, 6, 9, 7, 8, 0 }。

构造了初始堆后，我们来看一下完整的堆排序处理：

还是针对前面提到的无序序列 { 1,3, 4, 5, 2, 6, 9, 7, 8, 0 } 来加以说明。

相信，通过以上两幅图，应该能很直观的演示堆排序的操作处理。

核心代码

# 将列表打印成树（堆排序辅助函数）
import math

def printTree(lst):
    treeLen  = len(lst)
    treeLay = math.ceil(math.log2(treeLen + 1)) # 树层数
    index = 0
    treeWidth = 2 ** treeLay - 1    # 树宽度
    for i in range(treeLay):
        for j in range(2**i):
            print('{:^{}}'.format(lst[index], treeWidth), end=' ')
            index += 1
            if index >= treeLen:
                break
        treeWidth = treeWidth//2
        print()

lst = [1, 2, 3, 4, 5, 6, 7, 8, 9]
printTree(lst)

# 调整当前节点
def heap_adjust(n, i, array:list):  # array:list 表示array变量的类型是list
    '''
    调整当前节点核心算放
    :param n: 待比较数字的个数
    :param i: 当前节点的下标
    :param array: 待排序数据
    :return:None
    '''
    while 2 * i <= n:   # 性质5，=n只有左子树
        # 孩子结点判断2i为左孩子，2i+1为右孩子
        lChild_index = 2 * i
        maxChild_index = lChild_index # n=2i
        if n > lChild_index and array[lChild_index + 1] > array[lChild_index]:  # n>2i说明还有右孩子
            maxChild_index = lChild_index + 1   # n=2i+1
        # 和子树的根节点比较
        if array[maxChild_index] > array[i]:
            array[i], array[maxChild_index] = array[maxChild_index], array[i]   # 交换
            i = maxChild_index # 被交换后，需要判断是否还需要调整
        else:
            break
        printTree(array)
        print('--------------------------')

# 构建大顶堆
def maxHeap(total, array:list):
    for i in range(total//2, 0, -1):
        heap_adjust(total, i, array)    # 调整当前结点
    return array

total = 9
origin = [0,30, 20, 80, 40, 50, 10, 60, 70, 90]
print('maxHeap is ')
printTree(maxHeap(total, origin))

# 结论：第一层是最大值，第二层一定有个次大值

def HeapSort(input_list):
    
    #调整parent结点为大根堆
    def HeapAdjust(input_list,parent,length):
        
        temp = input_list[parent]
        child = 2*parent+1
        
        while child < length:
            if child+1 <length and input_list[child] < input_list[child+1]:
                child +=1
            
            if temp > input_list[child]:
                break
            input_list[parent] = input_list[child]
            parent = child
            child = 2*child+1
        input_list[parent] = temp
    
    if input_list == []:
        return []
    sorted_list = input_list
    length = len(sorted_list)
    #最后一个结点的下标为length//2-1
    #建立初始大根堆
    for i in range(0,length // 2 )[::-1]:
        HeapAdjust(sorted_list,i,length)
    
    for j in range(1,length)[::-1]:
        #把堆顶元素即第一大的元素与最后一个元素互换位置
        temp = sorted_list[j]
        sorted_list[j] = sorted_list[0]
        sorted_list[0] = temp
        #换完位置之后将剩余的元素重新调整成大根堆
        HeapAdjust(sorted_list,0,j)
        print('%dth' % (length - j))
        print(sorted_list)
    return sorted_list
    
        
if __name__ == '__main__':
    input_list = [50,123,543,187,49,30,0,2,11,100]
    print("input_list:")
    print(input_list)
    sorted_list = HeapSort(input_list)
    print("sorted_list:")
    print(input_list)



input_list:
[50, 123, 543, 187, 49, 30, 0, 2, 11, 100]
1th
[187, 123, 50, 49, 100, 30, 0, 2, 11, 543]
2th
[123, 100, 50, 49, 11, 30, 0, 2, 187, 543]
3th
[100, 49, 50, 2, 11, 30, 0, 123, 187, 543]
4th
[50, 49, 30, 2, 11, 0, 100, 123, 187, 543]
5th
[49, 11, 30, 2, 0, 50, 100, 123, 187, 543]
6th
[30, 11, 0, 2, 49, 50, 100, 123, 187, 543]
7th
[11, 2, 0, 30, 49, 50, 100, 123, 187, 543]
8th
[2, 0, 11, 30, 49, 50, 100, 123, 187, 543]
9th
[0, 2, 11, 30, 49, 50, 100, 123, 187, 543]
sorted_list:
[0, 2, 11, 30, 49, 50, 100, 123, 187, 543]

算法分析

堆排序算法的总体情况

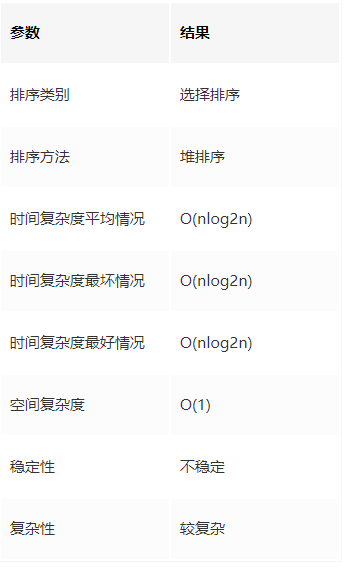
时间复杂度

堆的存储表示是顺序的。因为堆所对应的二叉树为完全二叉树，而完全二叉树通常采用顺序存储方式。

当想得到一个序列中第 k 个最小的元素之前的部分排序序列，最好采用堆排序。

因为堆排序的时间复杂度是 O(n+klog2n)，若 k ≤ n/log2n，则可得到的时间复杂度为 O(n)。

算法稳定性

堆排序是一种不稳定的排序方法。

因为在堆的调整过程中，关键字进行比较和交换所走的是该结点到叶子结点的一条路径，因此对于相同的关键字就可能出现排在后面的关键字被交换到前面来的情况。

归并排序

要点

归并排序是建立在归并操作上的一种有效的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

算法思想

将待排序序列 R[0…n-1] 看成是 n 个长度为 1 的有序序列，将相邻的有序表成对归并，得到 n/2 个长度为 2 的有序表；将这些有序序列再次归并，得到 n/4 个长度为 4 的有序序列；如此反复进行下去，最后得到一个长度为 n 的有序序列。

综上可知：

归并排序其实要做两件事：

• “分解”——将序列每次折半划分。

• “合并”——将划分后的序列段两两合并后排序。

我们先来考虑第二步，如何合并？

在每次合并过程中，都是对两个有序的序列段进行合并，然后排序。

这两个有序序列段分别为 R[low, mid] 和 R[mid+1, high]。

先将他们合并到一个局部的暂存数组R2 中，带合并完成后再将 R2 复制回 R 中。

为了方便描述，我们称 R[low, mid] 第一段，R[mid+1, high] 为第二段。

每次从两个段中取出一个记录进行关键字的比较，将较小者放入 R2 中。最后将各段中余下的部分直接复制到 R2 中。

经过这样的过程，R2 已经是一个有序的序列，再将其复制回 R 中，一次合并排序就完成了。

假如我们有一个n个数的数列，下标从0到n-1
首先是分开的过程
1 我们按照 n//2 把这个数列分成两个小的数列
2 把两个小数列 再按照新长度的一半 把每个小数列都分成两个更小的，一直这样重复，一直到每一个数分开了
比如： 6 5 4 3 2 1
第一次 n=6 n//2=3 分成 6 5 4 3 2 1
第二次 n=3 n//2=1 分成 6 5 4 3 2 1
第三次 n=1的部分不分了
n=2 n//2=1 分成 5 4 2 1
之后是合并排序的过程：
3 分开之后我们按照最后分开的两个数比较大小形成正确顺序后组合绑定
　　刚刚举得例子 最后一行最后分开的数排序后绑定 变成 4 5 1 2
　　排序后倒数第二行相当于把最新分开的数排序之后变成 6 4 5 3 12
4 对每组数据按照上次分开的结果，进行排序后绑定
　　6 和 4 5(两个数绑定了) 进行排序
　　3 和 1 2(两个数绑定了) 进行排序
　　排完后 上述例子第一行待排序的 4 5 6 1 2 3 两组数据
5 对上次分开的两组进行排序
　　拿着 4 5 6 1 2 3两个数组，进行排序，每次拿出每个数列中第一个(最小的数)比较，把较小的数放入结果数组。再进行下一次排序。
　　每个数组拿出第一个数，小的那个拿出来放在第一位 1 拿出来了， 变成4 5 6 2 3
　　每个数组拿出第一个书比较小的那个放在下一个位置 1 2被拿出来， 待排序 4 5 6 2
　　每个数组拿出第一个书比较小的那个放在下一个位置 1 2 3 被拿出来， 待排序 4 5 6
　　如果一个数组空了，说明另一个数组一定比排好序的数组最后一个大 追加就可以结果 1 2 3 4 5 6
　　相当于我们每次拿到两个有序的列表进行合并，分别从两个列表第一个元素比较，把小的拿出来，在拿新的第一个元素比较，把小的拿出来
　　这样一直到两个列表空了 就按顺序合并了两个列表

掌握了合并的方法，接下来，让我们来了解如何分解。

在某趟归并中，设各子表的长度为 gap，则归并前 R[0…n-1] 中共有 n/gap 个有序的子表：R[0…gap-1], R[gap…2gap-1], … , R[(n/gap)gap … n-1]。

调用 Merge 将相邻的子表归并时，必须对表的特殊情况进行特殊处理。

若子表个数为奇数，则最后一个子表无须和其他子表归并（即本趟处理轮空）：若子表个数为偶数，则要注意到最后一对子表中后一个子表区间的上限为 n-1。

核心代码

def merge_sort( li ):
    #不断递归调用自己一直到拆分成成单个元素的时候就返回这个元素，不再拆分了
    if len(li) == 1:
        return li

    #取拆分的中间位置
    mid = len(li) // 2
    #拆分过后左右两侧子串
    left = li[:mid]
    right = li[mid:]

    #对拆分过后的左右再拆分 一直到只有一个元素为止
    #最后一次递归时候ll和lr都会接到一个元素的列表
    # 最后一次递归之前的ll和rl会接收到排好序的子序列
    ll = merge_sort( left )
    rl =merge_sort( right )

    # 我们对返回的两个拆分结果进行排序后合并再返回正确顺序的子列表
    # 这里我们调用拎一个函数帮助我们按顺序合并ll和lr
    return merge(ll , rl)

#这里接收两个列表
def merge( left , right ):
    # 从两个有顺序的列表里边依次取数据比较后放入result
    # 每次我们分别拿出两个列表中最小的数比较，把较小的放入result
    result = []
    while len(left)>0 and len(right)>0 :
        #为了保持稳定性，当遇到相等的时候优先把左侧的数放进结果列表，因为left本来也是大数列中比较靠左的
        if left[0] <= right[0]:
            result.append( left.pop(0) )
        else:
            result.append( right.pop(0) )
    #while循环出来之后 说明其中一个数组没有数据了，我们把另一个数组添加到结果数组后面
    result += left
    result += right
    return result

if __name__ == '__main__':
    li = [5,4 ,3 ,2 ,1]
    li2 = merge_sort(li)
    print(li2)

算法分析

归并排序算法的性能

时间复杂度

归并排序的形式就是一棵二叉树，它需要遍历的次数就是二叉树的深度，而根据完全二叉树的可以得出它的时间复杂度是 O(n*log2n)。

空间复杂度

由前面的算法说明可知，算法处理过程中，需要一个大小为 n 的临时存储空间用以保存合并序列。

算法稳定性

在归并排序中，相等的元素的顺序不会改变，所以它是稳定的算法。

归并排序和堆排序、快速排序的比较

• 若从空间复杂度来考虑：首选堆排序，其次是快速排序，最后是归并排序。

• 若从稳定性来考虑，应选取归并排序，因为堆排序和快速排序都是不稳定的。

• 若从平均情况下的排序速度考虑，应该选择快速排序。

示例代码

基数排序、桶排序、计数排序

基数排序一般用于长度相同的元素组成的数组。首先按照最低有效数字进行排序，然后由低位向高位进行。基数排序可以看做是进行多趟桶排序。每个有效数字都在0-9之间，很适合桶排序，建10个桶很方便

[0,1)和[1,+∞)的桶排序是一种非常快速的排序，留置一个数组S，里面含有M个桶，初始化为0。然后遍历数组A，读入A_i时，S[A_i]增一。所有输入被读进后，扫描数组S得出排好序的表。该算法时间花费O(M+N)，空间上不能原地排序。

计数排序假设n个输入元素中每一个都是介于0到k之间的整数，此处k为某个整数。当k=O(n)时，计数排序的运行时间为Θ(n)。

对每一个数的元素x，确定出小于x的元素个数。有了这一信息就可以把x直接放到最终输出数组中的位置上。

要点

基数排序与本系列前面讲解的七种排序方法都不同，它不需要比较关键字的大小。

它是根据关键字中各位的值，通过对排序的 N 个元素进行若干趟“分配”与“收集”来实现排序的。

不妨通过一个具体的实例来展示一下，基数排序是如何进行的。

设有一个初始序列为: R {50, 123, 543, 187, 49, 30, 0 ,  2 , 11, 100}。

我们知道，任何一个阿拉伯数，它的各个位数上的基数都是以 0~9 来表示的。

所以我们不妨把 0~9 视为 10 个桶。

我们先根据序列的个位数的数字来进行分类，将其分到指定的桶中。例如：R[0] = 50，个位数上是 0，将这个数存入编号为 0 的桶中。

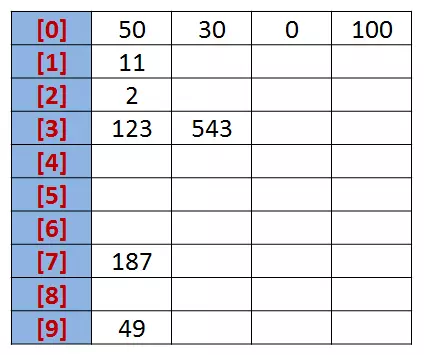
分类后，我们在从各个桶中，将这些数按照从编号 0 到编号 9 的顺序依次将所有数取出来。

这时，得到的序列就是个位数上呈递增趋势的序列。

按照个位数排序：{50, 30, 0, 100, 11, 2, 123, 543 , 187, 49}。

接下来，可以对十位数、百位数也按照这种方法进行排序，最后就能得到排序完成的序列。

算法分析

基数排序的性能

时间复杂度

通过上文可知，假设在基数排序中，r 为基数，d 为位数。则基数排序的时间复杂度为 O(d(n+r))。

我们可以看出，基数排序的效率和初始序列是否有序没有关联。

空间复杂度

在基数排序过程中，对于任何位数上的基数进行“装桶”操作时，都需要 n+r 个临时空间。

算法稳定性

在基数排序过程中，每次都是将当前位数上相同数值的元素统一“装桶”，并不需要交换位置。所以基数排序是稳定的算法。

示例代码

class bucketSort(object):
    def insertSort(self,a):
        n=len(a)
        if n<=1:
            pass
        for i in range(1,n):
            key=a[i]
            j=i-1
            while key<a[j] and j>=0:
                a[j+1]=a[j]
                j-=1
            a[j+1]=key
    def sort(self,a):
        n=len(a)
        s=[[] for i in xrange(n)]
        for i in a:
            s[int(i*n)].append(i)
        for i in s:
            self.insertSort(i)
        return [i for j in s for i in j]
    def __call__(self,a):
        return self.sort(a)
                       
if __name__=='__main__':
    from random import random
    from timeit import Timer
    a=[random() for i in xrange(10000)]
    def test_bucket_sort():
        bucketSort()(a)
    def test_builtin_sort():
        sorted(a)
    tests=[test_bucket_sort,test_builtin_sort]
    for test in tests:       
        name=test.__name__
        t=Timer(name+'()','from __main__ import '+name)
        print t.timeit(1)

import random
class bucketSort(object):
    def _max(self,oldlist):
        _max=oldlist[0]
        for i in oldlist:
            if i>_max:
                _max=i
        return _max
    def _min(self,oldlist):
        _min=oldlist[0]
        for i in oldlist:
            if i<_min:
                _min=i
        return _min
    def sort(self,oldlist):
        _max=self._max(oldlist)
        _min=self._min(oldlist)
        s=[0 for i in xrange(_min,_max+1)]
        for i in oldlist:
            s[i-_min]+=1
        current=_min
        n=0
        for i in s:
            while i>0:
                oldlist[n]=current
                i-=1
                n+=1
            current+=1
    def __call__(self,oldlist):
        self.sort(oldlist)
        return oldlist
if __name__=='__main__':
    a=[random.randint(0,100) for i in xrange(10)]
    bucketSort()(a)
    print a

import random
def radixSort():
    A=[random.randint(1,9999) for i in xrange(10000)]  
    for k in xrange(4):  #4轮排序      
        s=[[] for i in xrange(10)]
        for i in A:
            s[i/(10**k)%10].append(i)
        A=[a for b in s for a in b]
    return A

def countingSort(alist,k):
    n=len(alist)
    b=[0 for i in xrange(n)]
    c=[0 for i in xrange(k+1)]
    for i in alist:
        c[i]+=1
    for i in xrange(1,len(c)):
        c[i]=c[i-1]+c[i]
    for i in alist:
        b[c[i]-1]=i
        c[i]-=1
    return b
if __name__=='__main__':
    a=[random.randint(0,100) for i in xrange(100)]
    print countingSort(a,100)