池化层(Pooling layers)
除了卷积层,卷积网络也经常使用池化层来缩减模型的大小,提高计算速度,同时提高所提取特征的鲁棒性,我们来看一下。
先举一个池化层的例子,然后我们再讨论池化层的必要性。
假如输入是一个4×4矩阵,用到的池化类型是最大池化(max pooling)。
执行最大池化的树池是一个2×2矩阵。
执行过程非常简单,把4×4的输入拆分成不同的区域,我把这个区域用不同颜色来标记。
对于2×2的输出,输出的每个元素都是其对应颜色区域中的最大元素值。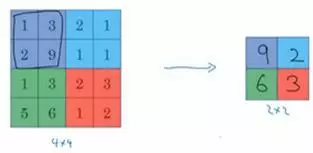
左上区域的最大值是9,右上区域的最大元素值是2,左下区域的最大值是6,右下区域的最大值是3。
为了计算出右侧这4个元素值,我们需要对输入矩阵的2×2区域做最大值运算。
这就像是应用了一个规模为2的过滤器,因为我们选用的是2×2区域,步幅是2,这些就是最大池化的超参数。
因为我们使用的过滤器为2×2,最后输出是9。
然后向右移动2个步幅,计算出最大值2。
然后是第二行,向下移动2步得到最大值6。
最后向右移动3步,得到最大值3。
这是一个2×2矩阵,即f=2,步幅是2,即s=2。
这是对最大池化功能的直观理解,你可以把这个4×4区域看作是某些特征的集合,也就是神经网络中某一层的非激活值集合。
数字大意味着可能探测到了某些特定的特征,左上象限具有的特征可能是一个垂直边缘,一只眼睛,或是大家害怕遇到的CAP特征。
显然左上象限中存在这个特征,这个特征可能是一只猫眼探测器。
然而,右上象限并不存在这个特征。
最大化操作的功能就是只要在任何一个象限内提取到某个特征,它都会保留在最大化的池化输出里。
所以最大化运算的实际作用就是,如果在过滤器中提取到某个特征,那么保留其最大值。
如果没有提取到这个特征,可能在右上象限中不存在这个特征,那么其中的最大值也还是很小,这就是最大池化的直观理解。
必须承认,人们使用最大池化的主要原因是此方法在很多实验中效果都很好。
尽管刚刚描述的直观理解经常被引用,不知大家是否完全理解它的真正原因,不知大家是否理解最大池化效率很高的真正原因。
其中一个有意思的特点就是,它有一组超参数,但并没有参数需要学习。
实际上,梯度下降没有什么可学的,一旦确定了f和s,它就是一个固定运算,梯度下降无需改变任何值。
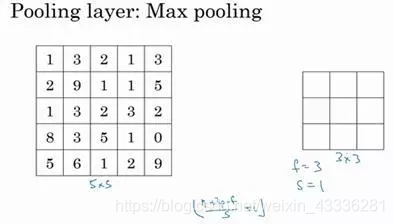
我们来看一个有若干个超级参数的示例,输入是一个5×5的矩阵。
我们采用最大池化法,它的过滤器参数为3×3,即f=3,步幅为1,s=1,输出矩阵是3×3。
之前讲的计算卷积层输出大小的公式同样适用于最大池化,
即(n+2p-f)/s+1,这个公式也可以计算最大池化的输出大小。
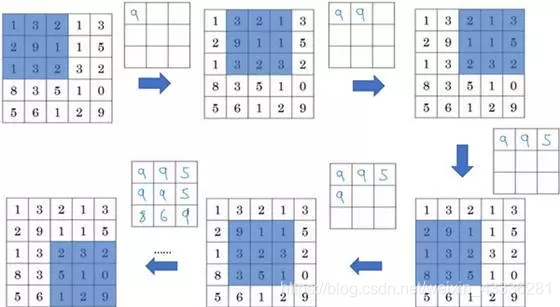
此例是计算3×3输出的每个元素,我们看左上角这些元素,注意这是一个3×3区域,因为有3个过滤器,取最大值9。
然后移动一个元素,因为步幅是1,蓝色区域的最大值是9。
继续向右移动,蓝色区域的最大值是5。
然后移到下一行,因为步幅是1,我们只向下移动一个格,所以该区域的最大值是9。
这个区域也是9。
这两个区域的最大值都是5。
最后这三个区域的最大值分别为8,6和9。
超参数f=3,s=1,最终输出如图所示。
以上就是一个二维输入的最大池化的演示,如果输入是三维的,那么输出也是三维的。
例如,输入是5×5×2,那么输出是3×3×2。
计算最大池化的方法就是分别对每个通道执行刚刚的计算过程。
如上图所示,第一个通道依然保持不变。
对于第二个通道,我刚才画在下面的,在这个层做同样的计算,得到第二个通道的输出。
一般来说,如果输入是5×5×n_c,输出就是3×3×n_c,n_c个通道中每个通道都单独执行最大池化计算,以上就是最大池化算法。
func MaxPooling(data [][]float64, pool_size int, step int)([][]float64){
result := [][]float64{}
for i := 0; i < len(data) - pool_size + 1; i += step{
temp := []float64{}
for j := 0; j < len(data[0]) - pool_size + 1; j += step{
var max_num float64 = 0
for cur_i := i; cur_i < i + pool_size; cur_i++{
for cur_j :=j; cur_j < j + pool_size; cur_j++{
max_num = math.Max(max_num, data[cur_i][cur_j])
}
}
temp = append(temp, max_num)
}
result = append(result, temp)
}
return result
}