信息学奥赛一本通（C++）在线评测系统——基础（一）C++语言—— 1058：求一元二次方程

时间限制: 1000 ms 内存限制: 65536 KB
提交数: 24853 通过数: 3925

【题目描述】

利用公式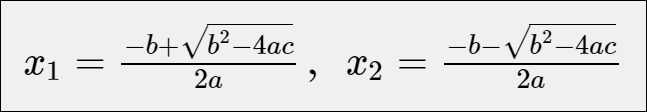，求一元二次方程ax²+bx+c=0的根，其中a不等于0。结果要求精确到小数点后5位。

【输入】

输入一行，包含三个浮点数a,b,c（它们之间以一个空格分开），分别表示方程ax2+bx+c=0的系数。

【输出】

输出一行，表示方程的解。
若两个实根相等，则输出形式为：“x1=x2=…”；
若两个实根不等，在满足根小者在前的原则，则输出形式为：“x1=…;x2=…”；
若无实根输出“No answer!”。
所有输出部分要求精确到小数点后5位，数字、符号之间没有空格。

【输入样例】

-15.97 19.69 12.02

【输出样例】

x1=-0.44781;x2=1.68075

【来源】

NO

代码

#include <iostream>
#include <cstdio>
#include <cmath>
#define precision_1 1e-12
#define precision_2 1e-6
using namespace std;
int main ()
{
    double a,b,c,x1,x2,delta;
    cin>>a>>b>>c;
    delta=b*b-4*a*c;//判别式
    if(delta<0&&fabs(delta)>precision_1)//当判别式小于给定的精度范围内，即delta<0时，无实根
        printf("No answer!\n");
    else if(fabs(delta)<precision_1)//当判别式小于给定的精度但>0，此时delta≈0
    {
        x1=-b/(2*a);
        if(fabs(x1)<precision_2) //超出所给的最小范围，此时，视为delta=0，直接输出0
            printf("x1=x2=%.5lf\n",0);
        else//未超出所给范围时，结果仍在小数点后5位有效数字以内，输出结果
            printf("x1=x2=%.5lf\n",x1);
    }
    else//delta>0时
    {
        x1=(-b+sqrt(delta))/(2*a);
        x2=(-b-sqrt(delta))/(2*a);
        if(fabs(x1)<precision_2)	x1=fabs(x1);//小于所给的最高精度，编译系统视为-0，求绝对值
        if(fabs(x2)<precision_2)	x2=fabs(x2);//小于所给的最高精度，编译系统视为-0，求绝对值
        if(x1<x2)//x1、x2中小的数在前输出
            printf("x1=%.5lf;x2=%.5lf",x1,x2);
        else
            printf("x1=%.5lf;x2=%.5lf",x2,x1);
    }
	return 0;
}