题意其他博客大概都描述了
说做法:
三种做法都是在一个把这题转换的前提下。
一、分析题
1. 数据范围 n * m 1e18,所以直观的对矩阵去跑大概率不行的。
2. 关注两个操作,一个操作是取两块+1, 另一种是一块+2。
因为可以进行无数次操作,我们发现只要所有数都是奇数或者都是偶数,即奇偶性相同。就可通过+2操作使得都相同。
那么+1操作可以干什么呢?改变奇偶性。
3. 因为每次+1可以改变一对奇偶性。所以我们观察到,如果n*m为奇数,那么代表有这n*m一定有奇数个(偶数或奇数)那么对应的就有偶数个(奇数或偶数)
那么我们一定可以通过+1操作使得这偶数个(奇数或偶数)翻转奇偶性,使得所有数奇偶性相同。
所以n*m为奇数时可以填任何数。
4. n*m为偶数的时候就不那么好分析了。我们发现n*m为偶数的时候一定得保证构成有偶数个奇数和偶数个偶数
不过至此,我们可以把这个问题转换为n*m格子,每个格子可以填[L,R]范围内的数字,问使得最后填好的方案每个偶数和奇数都成对出现。
剩下三个做法都是对于n*m为偶数的情况下的做法
二、做法1(官方题解做法1)
组合数学。抄一下官方题解的公式(懒得写了)在L,R内,E为偶数个数,O就为奇数个数
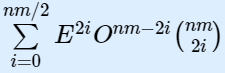
二项式定理:
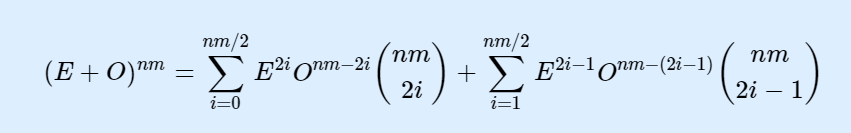
(E - O)^nm = (E + (-O))^nm
那这两项刚好可以把后面尾缀删掉。
https://paste.ubuntu.com/p/cmJnqw7rfY/
三、做法2(官方题解2)
这个我似懂非懂
https://paste.ubuntu.com/p/Vq6mjX3Hxs/
三、做法3 dp + 矩阵快速幂
其实这个做法我认为最简单且直观。
设dpi0 表示填了i个有偶数个偶数,和 dpi1 表示填了i个有奇数个偶数
转移方程就是:
dpi0 = dpi1 * even + dpi0 * odd;
dpi1 = dpi0 * even + dpi1 * odd;
但是要填1e18个,这个转移式子就可以用矩阵快速幂来加速。
写法1:https://paste.ubuntu.com/p/PSc2DTytmb/
写法2 :https://paste.ubuntu.com/p/38Pc5ydSMk/
详细讲解看我B站