用贪心算法解决马踏棋盘问题

用贪心算法解决马踏棋盘问题时，主要的思想与用递归的方法解决该问题相同，都是用深度优先搜索，只是在选下一个结点的时候做了贪心算法优化，其思路如下：

从起始点开始，根据“马”的走法，它的下一步的可选择数是有0—8个的。

已知，当马下一步的可选择数为0的时候(即马没有下一个节点可跳)，进行回溯。当下一步的可选择数有1个的时候，我们直接取那一步就可以。但是如果下一步的可选择数有多个的时候呢？

在之前用的递归+回溯算法中，我们是任意取一个的，只要它在棋盘内，且未遍历就可以了。但其实我们怎么选下一步，对搜索的效率影响是非常大的！

贪心算法：又称贪婪算法，是指在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的局部最优解。

用贪心算法的思想来解决在棋盘如何选择下一个节点的问题，就是计算马儿的哪个下一节点对应的下一个节点（即下下个节点）的总数最少，就将哪个下一节点视为最优。

例如：假设a、b、c、d为马儿可以选择的下一个节点，选哪个比较好，就看哪个点的后续下一步比较少。如果马走到a点后的下一步有3个选择；而b的下一步有2个；c有1个，d有2个，那么最优选择是：c点。

因为c点的后续下一步很少，如果不先遍历它的话以后可能会很难遍历到它。甚至极端一点的情况是，如果现在不遍历它，以后都遍历不到了。遍历不成功的时候只能回溯，一直回溯到此刻的点，然后选了c点以后才能完成，这就浪费了大量的时间。

选择下一个节点的函数如下图所示，其中，num是马在当前位置时，下一个节点的数目。数组a[]的长度为num，a[]中存放马的每个下一节点所对应的下一个节点的数目。

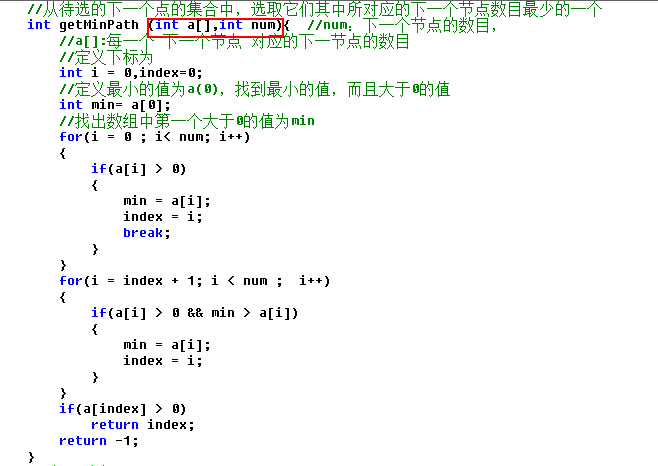
用贪心算法求解马踏棋盘问题的一个解的代码如下。当然，一般来讲棋盘的大小应该为8*8，此处，定义的是6*6,主要是为了方便和我之前的用递归+回溯的方法写的代码进行对比，用递归的话，用8*8的棋盘，执行的时间有点长，于是就用了6*6的.

    # include <stdio.h>  
    # include <stdlib.h>  
    # include <math.h>  
    # include <time.h>
    # define R 6  
    # define C 6  
    int cheesboard [R] [C];  
    const int moveX [8] = {-2,-1,1,2,2,1,-1,-2};  
    const int moveY [8] = {1,2,2,1,-1,-2,-2,-1};  
    //初始化棋盘,将棋盘所有的位置赋值为0  
    void initBoard (int board[][C]){  
        int i ,j;
        for(i = 0; i < R; i ++){  
            for( j = 0; j < C; j ++){  
                board[i][j] = 0;  
            }  
        }  
    }
    //从待选的下一个点的集合中，选取它们其中所对应的下一个节点数目最少的一个
    int getMinPath (int a[],int num){  //num：下一个节点的数目，
        //a[]:每一个 下一个节点 对应的下一节点的数目
        //定义下标为  
        int i = 0,index=0;  
        //定义最小的值为a(0)，找到最小的值，而且大于0的值  
        int min= a[0];  
        //找出数组中第一个大于0的值为min
        for(i = 0 ; i< num; i++)  
        {  
            if(a[i] > 0)  
            {  
                min = a[i];  
                index = i;  
                break;  
            }  
        }  
        for(i = index + 1; i < num ;  i++)  
        {  
            if(a[i] > 0 && min > a[i])  
            {  
                min = a[i];  
                index = i;  
            }  
        }  
        if(a[index] > 0)  
            return index;  
        return -1;  
    }
    // 打印路径  
    void printPath (int board[][C]){  
        int i,j;  
        for (i = 0; i < R; i++){  
            for ( j = 0; j < C; j++){  
                printf("%d	",board[i][j]);  
            }  
            printf("

");  
        }  
    }  
    // 获得马行走的路径  
    void getPath (int board [][C], int startX, int startY){  
        //下一个可行位置的数目
        int next = 0;  
        //路径最短的可行位置在数组中的位置  
        int min;  
        //下一个可行位置的可行位置数目  
        int nextNext;  
        //将棋盘初始化  
        initBoard (board);  
        // 存放下一个位置对应的下一个位置的数目  
        int nextNum[8] = {0,0,0,0,0,0,0,0};  
        //下一个位置的在二维数组中对应位置，初始为0  
        int nextX[C] = {0};  
        int nextY[R] = {0};  
        //第一个位置赋值为1  
        board [startX] [startY] = 1;  
        int m,i,j;  
        //走完所有的点要循环63次  
        for ( m = 1; m < R*C; m++){  
                //当前点其后面可行的位置设为0  
                next = 0;  
        //通过循环来判断该位置是否还可以向下面位置移动  
        for ( i =  0; i < 8; i++){  
            if(startX + moveX[i] < 0 || startX + moveX[i] >= R  
                || startY + moveY[i] < 0 || startY + moveY[i] >= C 
                || board[startX+moveX[i]][startY+moveY[i]] != 0){  
                    continue;  
                }
                //如果可以向下一个位置移动的话，通过next数组保存下来，通过next记录下有多少个  
            nextX [next] = startX + moveX[i];  
            nextY [next] = startY + moveY[i];  
            next ++;  
        }  
        //循环结束之后，对next的值进行判断，当为1的时候  
        if (next == 1){  
            //让min=0，表示现在所需要的位置是在我们的保存next数组中的第一位  
            min = 0;  
        //设置初始点  
            goto set_nextpoint;  
        }  
        //无法向下一个位置移动了  
        else if (next == 0){  
            printf("没有路径可走了
");  
            goto print_path;  
        }  
        else {  
                /*当有多个路径可以走的时候,检测每一个点还可不可以继续向下走然后 
                记录下来该点有几个点可以向下走，找到最少的一个但是不为0的哪一个 
                */  
            for (i = 0; i<next; i++){  
                nextNext = 0;  
                for(j = 0; j < 8; j++){  
                    if(nextX[i] + moveX[j] >=0 && nextX[i] + moveX[j] < R  
                        && nextY[i] + moveY[j] >= 0 && nextY[i] + moveY[j] <C  
                        && board [nextX[i]+moveX[j]][nextY[i]+moveY[j]] == 0){  
                            nextNext ++;
                        }
                }  
                nextNum[i] = nextNext;  
            }  
            if ((min = getMinPath(nextNum,next))>=0 )  
            {  
                goto set_nextpoint;  
            }  
            else{  
                printf("没有路径可走了
");  
                goto print_path;  
            }  
        }  
    set_nextpoint:  
            startX = nextX[min];  
            startY = nextY[min];  
            board[startX][startY] = m+1;  
        }  
    print_path:  
        printPath(board);  
      
    }  
     void judgeExistence(){
            if(R<=4 || C<=4){//通过已有的理论给出判断条件
                printf("棋盘矩阵为%d * %d 时，马从其中一些节点出发，不能够找到"
                    "
不重复遍历完棋盘中每一格的路径.请重新设置矩阵的大小，矩"
                    "
阵的大小应满足行数和列数均大于4
",R,C);
                exit(0);
            }
        }
    int main (){  
        int i,j;  
        //main函数后首先执行一个判断存在性的函数    
        judgeExistence();
        clock_t start, finish;  //计算核心方法一共花费了多少时间
        long duration;

        //获得最开始的位置  
        label_1:printf("请输入马初始横坐标(X<=%d):X=
",R);
        scanf("%d",&i);
        if(i>R){
            printf("请输入小于等于%d的数
",R);
            goto label_1;
        }
        label_2:printf("请输入马初始纵坐标(Y<=%d):Y=
",C);
        scanf("%d",&j);
        if(j>C){
            printf("请输入小于等于%d的数
",C);
            goto label_2;
        }
        start=clock();//开始时间
        i=i-1;
        j=j-1;
    
        //调用该函数获取路径  
        getPath(cheesboard, i, j); 
        finish=clock();
        duration=finish-start;
        printf("棋盘的大小为%d*%d
",R,C);
        printf("采用贪心算法所需的时间为%ld	 ms 
",duration);
        return 0;
    }