并查集深入分析

什么是并查集？

　　并查集（Union-find Sets）是一种非常精巧而实用的数据结构，它主要用于处理一些不相交集合的合并问题。一些常见的用途有求连通子图、求最小生成树的 Kruskal 算法和求最近公共祖先（Least Common Ancestors, LCA）等。

　　使用并查集时，首先会存在一组不相交的动态集合 S={S1,S2,⋯,Sk}，一般都会使用一个整数表示集合中的一个元素。

　　每个集合可能包含一个或多个元素，并选出集合中的某个元素作为代表。每个集合中具体包含了哪些元素是不关心的，具体选择哪个元素作为代表一般也是不关心的。我们关心的是，对于给定的元素，可以很快的找到这个元素所在的集合（的代表），以及合并两个元素所在的集合，而且这些操作的时间复杂度都是常数级的。

　　并查集的实现原理也比较简单，就是使用树来表示集合，树的每个节点就表示集合中的一个元素，树根对应的元素就是该集合的代表，如图 1 所示。

图 1 并查集的树表示

　　图中有两棵树，分别对应两个集合，其中第一个集合为 {a,b,c,d}，代表元素是 a；第二个集合为 {e,f,g}，代表元素是 e。

　　树的节点表示集合中的元素，指针表示指向父节点的指针，根节点的指针指向自己，表示其没有父节点。沿着每个节点的父节点不断向上查找，最终就可以找到该树的根节点，即该集合的代表元素。

并查集基本操作

基本操作有三个：

1. makeSet(n)：建立一个新的并查集，其中包含n个单元素集合。
2. find(x)：找到元素 x 所在的集合的代表，该操作也可以用于判断两个元素是否位于同一个集合，只要将它们各自的代表比较一下就可以了。
3. unionSet(x, y)：把元素x和元素y所在的集合合并，要求x和y所在的集合不相交，如果相交则不合并。

操作一：建立新的并查集，使得其中每个元素都是一个单元素集合，即父节点是其自身。

操作二：找到集合代表，如果每次都沿着父节点向上查找，那时间复杂度就是树的高度，完全不可能达到常数级。这里需要应用一种非常简单而有效的策略——路径压缩。路径压缩，就是在每次查找时，令查找路径上的每个节点都直接指向根节点，如图 3 所示。有递归和非递归两个版本。

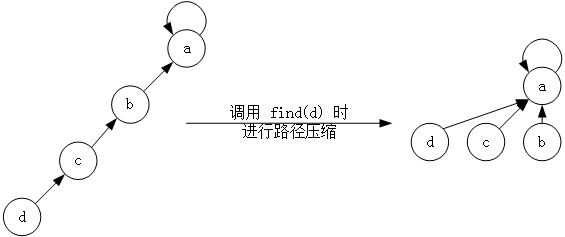
操作三：合并集合，并查集的合并也非常简单，就是将一个集合的树根指向另一个集合的树根，如图 4 所示。

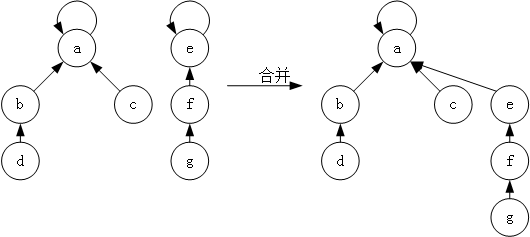
这里有一个问题，那就是这两个树，谁并向谁呢？

一般来说，按秩合并。该方法使用秩来表示树高度的上界，在合并时，总是将具有较小秩的树根指向具有较大秩的树根。简单的说，就是总是将比较矮的树作为子树，添加到较高的树中。为了保存秩，需要额外使用一个与 uset 同长度的数组，并将所有元素都初始化为 0。下面是按秩合并的完整代码，包含递归和非递归的find操作：

const int MAXSIZE = 500;
int uset[MAXSIZE];
int rank[MAXSIZE];//
 
void makeSet(int size)//操作一：建立并查集
{
    for(int i = 0;i < size;i++)  uset[i] = i;
    for(int i = 0;i < size;i++)  rank[i] = 0;
}
int find1(int x)//递归
{
    if (x != uset[x]) uset[x] = find(uset[x]);
    return uset[x];
}
int find2(int x)//非递归
{
    int p=x,tmp;
    while(uset[p]!=p)//找到集合代表
        p=uset[p];
    while(x!=p)//路径压缩
    {
        tmp=uset[x];
        uset[x]=p;
        x=tmp;
    }
    return x;
}
void unionSet(int x, int y)//操作三：合并
{
    if ((x = find(x)) == (y = find(y))) return;
    if (rank[x] > rank[y]) uset[y] = x;
    else {
        uset[x] = y;
        if (rank[x] == rank[y]) rank[y]++;
    }
}

还有一种方法，按树的结点个数大小合并，小的树并向大的树。这样的并查集具有一个略微不同的定义，即若 uset 的值是正数，则表示该元素的父节点（的索引）；若是负数，则表示该元素是所在集合的代表（即树根），而且值的相反数即为集合中的元素个数。相应的代码如下所示，同样包含递归和非递归的 find 操作：

const int MAXSIZE = 500;
int uset[MAXSIZE];

void makeSet(int size)//操作一：建立并查集
{
    for(int i = 0;i < size;i++)
        uset[i] = -1;
}
int find1(int x)//递归
{
    if(uset[x]<0) return x;
    uset[x]=find(uset[x]);
    return uset[x];
}
int find2(int x)//非递归
{
    int p=x,t;
    while(uset[p]>=0)
        p=uset[p];
    while(x!=p)
    {
        t=uset[x];
        uset[x]=p;
        x=t;
    }
    return x;
}
void unionSet(int x, int y)//操作三：合并
{
    if ((x = find(x)) == (y = find(y))) return;
    if (uset[x] < uset[y])
    {
        uset[x] += uset[y];
        uset[y] = x;
    }
    else
    {
        uset[y] += uset[x];
        uset[x] = y;
    }
}

并查集分析

并查集的空间复杂度是 O(n) 的，这个很显然，如果是按秩合并的，占的空间要多一些。find 和 unionSet 操作都可以看成是常数级的，或者准确来说，在一个包含 nn 个元素的并查集中，进行 mm 次查找或合并操作，最坏情况下所需的时间为 O(mα(n))，这里的 α 是 Ackerman 函数的某个反函数，在极大的范围内（比可观察到的宇宙中估计的原子数量 1080 还大很多）都可以认为是不大于 4 的。具体的时间复杂度分析，请参见《算法导论》的 21.4 节 带路径压缩的按秩合并的分析。

特别鸣谢，本文参考：http://www.cnblogs.com/cyjb/p/UnionFindSets.html

特别推荐，趣味讲解并查集：http://blog.csdn.net/dellaserss/article/details/7724401

作者： AlvinZH

出处： http://www.cnblogs.com/AlvinZH/

本人Github：https://github.com/Pacsiy/JobDu

本文版权归作者AlvinZH和博客园所有，欢迎转载和商用，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。