本文所有算法采用vs2010环境c++语言编写,使用公共头如下。
在线提交时 #include "stdafx.h" 需要去掉。
1 #include "stdafx.h" 2 #include"iostream" 3 #include"vector" 4 #include"iterator" 5 #include"algorithm" 6 #include"vector" 7 #include"string" 8 #include"memory.h" 9 #include"stdlib.h" 10 #include"queue" 11 #include"math.h" 12 #include"list" 13 using namespace std;
本文全部的树节点的定义如下:
1 class TreeNode { 2 public: 3 int val; 4 TreeNode *left, *right; 5 TreeNode(int val) { 6 this->val = val; 7 this->left = this->right = NULL; 8 } 9 };
递归
打印合法的括号对
1 void print(int left,int right,vector<int>temp){ 2 if(left==0&&right==0){ 3 for(int i=0;i<temp.size();i++){ 4 if(temp[i]==0) 5 cout<<"("; 6 if(temp[i]==1) 7 cout<<")"; 8 } 9 cout<<endl; 10 return ; 11 } 12 if(left>0){ 13 temp.push_back(0); 14 print(left-1,right,temp); 15 temp.pop_back(); 17 } 18 if(right>0&&left<right){ 19 temp.push_back(1); 20 print(left,right-1,temp); 21 temp.pop_back(); 22 } 24 } 25 int printBracketMain(){ 26 vector<int> temp; 27 print(3,3,temp); 28 return 0; 29 }
判断一棵树是否是另一颗的子树
1 class Solution { 2 public: 3 bool isPart(TreeNode *T1, TreeNode *T2){ 4 if(T2==NULL) 5 return true; 6 if(T1==NULL) 7 return false; 8 if(T1->val==T2->val) 9 return isPart(T1->right,T2->right)&&isPart(T1->left,T2->left); 10 return false; 11 } 12 13 bool isSubtree(TreeNode *T1, TreeNode *T2) { 14 bool ispart = false; 15 if(T1!=NULL){ 16 if(T1->val==T2->val) 17 ispart = isPart(T1,T2); 18 if(!ispart) 19 ispart = isSubtree(T1->left,T2); 20 if(!ispart) 21 ispart = isSubtree(T1->right,T2); 22 } 23 return ispart; 24 } 25 };
判断一棵树是不是平衡二叉树
1 class Solution { 2 public: 3 int getMax(int a,int b){ 4 return a>=b?a:b; 5 } 6 int getAbs(int a){ 7 return a<0?-a:a; 8 } 9 int height(TreeNode *root){ 10 if(root==NULL) return 0; 11 int leftH = height(root->left)+1; 12 int rightH = height(root->right)+1; 13 if(leftH==-1||rightH==-1) 14 return -1; 15 if(abs(leftH-rightH)>1) 16 return -1; 17 return getMax(leftH,rightH); 18 } 19 bool isBalanced(TreeNode *root) { 20 int isBalance = height(root); 21 if(isBalance==-1) 22 return false; 23 return true; 24 } 25 };
字符串
KMP
贪心
动态规划
最长上升子序列
1 int longestIncreasingSubsequence(vector<int> nums) { 2 int len = nums.size(); 3 vector<int> ans(nums.size(),1);; 4 int maxlen = 0; 5 ans[0] = 1; 6 for(int i=0;i<len;i++){ 7 for(int j=0;j<i;j++){ 8 if(nums[j]<nums[i]) 9 ans[i] = max(ans[i],ans[j]+1); 10 } 11 if(ans[i]>maxlen) 12 maxlen = ans[i]; 13 } 14 return maxlen; 15 } 16 int LisMain(){ 17 vector<int> nums; 18 int n=0,temp=0; 19 cin>>n; 20 while(n--){ 21 cin>>temp; 22 nums.push_back(temp); 23 } 24 int len = longestIncreasingSubsequence(nums); 25 cout<<len<<endl; 26 return 0; 27 }
01背包问题
01背包问题比较经典,下面是常规解法

1 int backPack(int m, vector<int> A) { 2 int len =A.size(); 3 vector<int> B; 4 long sum=0; 5 for(int i=0;i<len;i++){ 6 if(A[i]<=m){//cut 7 B.push_back(A[i]); 8 if(sum<m) 9 sum+=A[i]; 10 } 11 } 12 if(sum<=m)//cut 13 return sum; 14 15 len = B.size(); 16 int **dp = new int*[len+1] ; 17 for(int i=0;i<=len;i++){ 18 dp[i] = new int[m+1]; 19 } 20 for(int ii=0;ii<=len;ii++){ 21 for(int jj=0;jj<=m;jj++) 22 dp[ii][jj]=0; 23 } 24 25 for(int i=1;i<=len;i++){ 26 int a = B[i-1]; 27 for(int j=0;j<a;j++) 28 dp[i][j] = dp[i-1][j]; 29 for(int j=a;j<=m;j++){ 30 dp[i][j] = max(dp[i-1][j],dp[i-1][j-a]+a); 31 if(dp[i][j]==m)//cut 32 return m; 33 } 34 } 35 //debug 36 for(int ii=1;ii<=len;ii++){ 37 for(int jj=0;jj<=m;jj++) 38 cout<<dp[ii][jj]<<" "; 39 cout<<endl; 40 } 41 cout<<endl; 42 return dp[len][m]; 43 }
输入背包容量:10
物品价值和体积相等 3,4,8,5
结果:
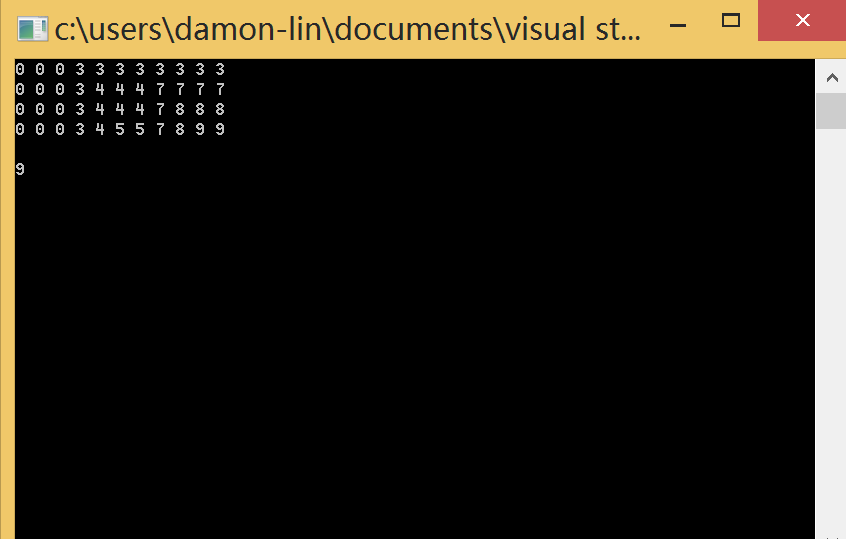
上面算法的时间复杂度已经最优,但是空间复杂度可以优化,因为有这样一个事实:每次计算只需知道前一次的最优解即可推出现在的最优解。同时推算顺序如下图所示:

都是从小到大,如上图中:a到b,b到c..... 这样需要多一行来保存新的最优解,但是如果顺寻颠倒,从最大到最小,先求f,求完后立马覆盖,再求e,这时已经用不到f了,所以不会影响,那么可以优化成一行。所以最后的空间复杂度为O(n)。

1 int backPack(int m, vector<int> A) { 2 int len =A.size(); 3 vector<int> B; 4 long sum=0; 5 for(int i=0;i<len;i++){ 6 if(A[i]<=m){//cut 7 B.push_back(A[i]); 8 if(sum<m) 9 sum+=A[i]; 10 } 11 } 12 if(sum<=m)//cut 13 return sum; 14 15 len = B.size(); 16 int *dp = new int[m+1] ; 17 18 for(int ii=0;ii<=m;ii++) 19 dp[ii]=0; 20 21 for(int i=1;i<=len;i++){ 22 int a = B[i-1]; 23 for(int j=m;j>=a;j--){ 24 dp[j] = max(dp[j],dp[j-a]+a); 25 if(dp[j]==m)//cut 26 return m; 27 } 28 //debug 29 for(int ii=1;ii<=m;ii++){ 30 cout<<dp[ii]<<" "; 31 } 32 cout<<endl; 33 } 34 35 return dp[m]; 36 }
字符串编辑距离
这也是一个很金典的动态规划问题,给定两个字符串a,b长分别为n和m,计算经过多少步编辑步骤可以使两个字符串相同。
编辑步骤可以是
1】删除其中一个字符串中的一个字符
2】增加一个字符到一个字符串中
3】改变一个字符串中的一个字符
我们设这个问题的状态为 dp[i][j] 表示两个字符串的长度分别为i和j时最少需要多少步编辑步骤。这样我们就可以把问题缩小,从(0,0)->(n,m) 。
接下来就是确定动态方程,我们先考虑dp[i][j]时a[i]和b[j]要么相等要么不等。如果相等,可以把这个字符忽略掉,那么dp[i][j] = dp[i-1][j-1]。如果不相等,我们可以删除a[i],把问题减小到dp[i-1][j]的规模;也可以删除b[j]得到dp[i][j-1]这个状态;或者干脆直接修改使a[i]==b[j],这样就是dp[i-1][j-1];要注意一点不需要考虑增加这种情况,因为他和删除的效果一样!
所以我们可以得到递推方程: dp[i][j] = min(dp[(i-1)][j]+1,dp[i][j-1]+1,dp[(i-1)][j-1]+1);
最后来考虑初始化的问题,这时候先来看看我们的定义:dp[i][j] 表示两个字符串的长度分别为i和j时最少需要多少步编辑步骤。那么dp[0][0] = 0 只需0步,一个字符串为空的时候需要另一个字符串长度步,所以dp[0][i] = i,dp[0][j] = j
具体代码:

1 int min(int a,int b,int c){ 2 int t = a<b?a:b; 3 return t<c?t:c; 4 } 5 int minDistance(string word1, string word2) { 6 int n = word1.length(); 7 int m = word2.length(); 8 if(n==0||m==0) 9 return m==0?n:m; 10 int **dp = new int*[2];//roll array 11 for(int i=0;i<2;i++){ 12 dp[i] = new int[m+1]; 13 } 14 for(int j=0;j<=m;j++){//word1=''and word2='1';word2='12';word2='123';word2='123...' 15 dp[0][j] = j; 16 } 17 for(int i=1;i<=n;i++){ 18 for(int j=1;j<=m;j++){ 19 dp[i&1][0] = i; 20 if(word1[i-1]==word2[j-1]){//0-n 0-m 21 dp[i&1][j] = dp[(i-1)&1][j-1]; 22 }else{ 23 dp[i&1][j] = min(dp[(i-1)&1][j]+1,dp[i&1][j-1]+1,dp[(i-1)&1][j-1]+1); 24 } 25 cout<<dp[i&1][j]<<" "; 26 } 27 cout<<endl; 28 } 29 return dp[n&1][m]; 30 }
图论
迪杰斯特拉:
1 int dis[1001][1001]; 2 int set[1001]; 3 int path[1001]; 4 #define INF 9999999; 5 6 void init(){ 7 for(int i=0;i<1001;i++) 8 for(int j=0;j<1001;j++) 9 dis[i][j]=INF; 10 } 11 12 void printPath(int begin,int end,int N){ 13 stack<int> s; 14 int i=end; 15 while(path[i]!=0){ 16 s.push(path[i]); 17 i = path[i]; 18 } 19 cout<<begin<<" "; 20 while(!s.empty()){ 21 cout<<s.top()<<" "; 22 s.pop(); 23 } 24 cout<<end<<" "; 25 } 26 27 void djs(int start,int end,int N){ 28 while(true){ 29 int min=INF; 30 int index=0; 31 //find min 32 for(int i=1;i<=N;i++){ 33 if(i!=start&&set[i]==0) 34 if(dis[start][i]<min){ 35 min = dis[start][i]; 36 index = i; 37 } 38 } 39 if(index==0)//no ans 40 break; 41 set[index]=1;//set the flag 42 for(int i=1;i<=N;i++){ 43 if(i!=start) 44 if(dis[start][i]>dis[start][index]+dis[index][i]){ 45 dis[start][i] = dis[start][index]+dis[index][i]; 46 path[i] = index; 47 } 48 } 49 } 50 } 51 52 int djsMain(){ 53 int N=0,M=0,S=0,T=0; 54 init(); 55 cin>>N>>M>>S>>T;//node edge start end 56 int temp=0,s=0,e=0; 57 for(int i=0;i<M;i++){ 58 cin>>s>>e>>temp; 59 if((dis[s][e]>temp)){ 60 dis[s][e]=temp; 61 dis[e][s]=temp; 62 } 63 } 64 djs(S,T,N); 65 cout<<dis[S][T]<<endl; 66 //printPath(S,T,N); 67 return 0; 68 }
弗洛伊德:
1 #define N 1001 2 #define INF 99999 3 int dis[N][N]; 4 5 void initDis(){ 6 for(int i=0;i<N;i++) 7 for(int j=0;j<N;j++){ 8 if(i==j) 9 dis[i][j] = 0; 10 else 11 dis[i][j] = INF; 12 } 13 } 14 void output(int n){ 15 for(int i=1;i<=n;i++){ 16 for(int j=1;j<=n;j++) 17 { 18 if(j!=1) 19 cout<<" "; 20 cout<<dis[i][j]; 21 } 22 cout<<endl; 23 } 24 } 25 void floyd(int n){ 26 for(int k=1;k<=n;k++) 27 for(int i=1;i<=n;i++) 28 for(int j=1;j<=n;j++) 29 { 30 if(dis[i][j]>dis[i][k]+dis[k][j]) 31 dis[i][j] = dis[i][k]+dis[k][j]; 32 } 33 } 34 35 int floydMain(){ 36 int n=0,m=0; 37 initDis(); 38 int temp = 0,i=0,j=0; 39 while(cin>>n>>m){ 40 for(int k=0;k<m;k++){ 41 cin>>i>>j>>temp; 42 if(temp<dis[i][j]){ 43 dis[i][j] = temp; 44 dis[j][i] = temp; 45 } 46 } 47 floyd(n); 48 output(n); 49 } 50 return 0; 51 }
数论
