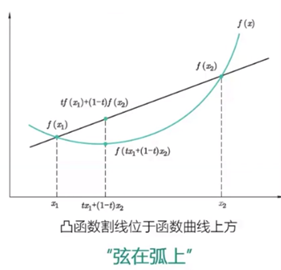
凸函数：假设f(x)为多元函数，如果对任意t∈[0,1]，均满足：
。则称f(x)为凸函数。
Jensen不等式：如果f是凸函数，X是随机变量，则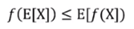
。
该不等式的另一种描述：
。ai表示权重。取等号的条件是：f(xi)是常量。
凸函数图示：
聚类
本质：将数据集中相似的样本进行分组的过程。
簇：分组后每个组称为一个簇，每个簇的样本对应一个潜在的类别。样本没有类别标签，因此是聚类一种典型的无监督学习方法。
簇的条件：相同簇的样本之间距离较近；不同簇的样本之间距离较远。
聚类方法：层次聚类，K-Means，谱聚类等等。
算法介绍
K-Means模型：
起源：最初起源于信号处理，是一种比较流行的聚类方法。
数据集：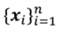
，将样本划分为k个簇，每个簇中心为cj(1<=j<=k)。
优化目标：最小化所有样本点到所属簇中心的距离平方和（失真度量）。
模型求解：
公式中rij是离散形式，优化使用图示中的交替迭代法。
固定c，优化r：
优化目标：
不同的Ji(ri)相互独立，可以分别优化：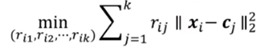
对于样本xi，对最近的中心j，rij=1，将其指派给最近的类。
固定r，优化c：
优化目标：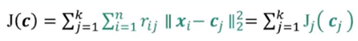
不同的Jj(cj)相互独立，分别优化，且均为二次凸函数：
分母（蓝色）表示cj这一类里总共有多少样本，分子（绿色）表示对应的第j类中每一个样本的求和。因此结果为第j类中心为j类样本均值。
K-Means算法流程：
1， 随机选择k个点作为初始中心。
2， Repeat：将每个样本指派到最近的中心，形成k个类；重新计算每个类的中心为该类样本均值。
3， 直到中心不发生变化。
高斯混合模型（GMM）：
GMM求解：
应用到Jensen不等式，注意优化目标中是ln函数，在函数图像上显示为凹函数，因此原Jensen不等式表示
中，将<=改为>=。（即第二行）
EM算法：
