斯坦福CS224n作业一
softmax
作业要求如下:

解析:题目要求我们证明(softmax)函数具有常数不变性。
解答:对于(x+c)的每一维来说,有如下等式成立:
[softmax(x+c)_{i}=frac{e^{x_{i}+c}}{sum_{j}e^{x_{j}+c}}=frac{e^{x_{i}}*e^{c}}{sum_{j}(e^{x_{j}}*e^{c})}=frac{e^{x_{i}}*e^{c}}{sum_{j}(e^{x_{j}})*e^{c}}=frac{e^{x_{i}}}{sum_{j}e^{x_{j}}}=softmax(x)_{i}
]
则可知(softmax(x)=softmax(x+c))成立
Neural Network Basics
求解sigmoid函数梯度
作业要求如下:

解析:本题要求我们计算(sigma(x))函数的梯度,并用(sigma(x))表示结果
解答:$$frac{partial{(sigma(x)})}{partial{x}}=frac{partial{(frac{1}{1+e^{-x}}})}{partial{x}}$$
设(a=1+e^{-x}),应用链式法则可以得到:
[frac{partial{(sigma(x)})}{partial{x}}=frac{partial{(frac{1}{a}})}{partial{x}}=-(frac{1}{a})^{2}*frac{partial{a}}{partial{x}}=-(frac{1}{a})^{2}*e^{-x}*(-1)=frac{e^{-x}}{(1+e^{-x})^{2}}
]
用(sigma(x))可以表示为(sigma(x)-sigma(x)^{2})
softmax + 交叉熵的梯度推导
作业要求如下:

解析:本题给定了实际值(y),预测值(hat{y}),以及softmax的输入向量( heta),要求我们求解(CE(y,hat{y}))对( heta)的梯度
解答:
对于每个( heta_{i})来说,(CE(y,hat{y}))对( heta_{i})的梯度如下所示:

可知,对于所有的i来说,(CE(y,hat{y}))对( heta_{i})的梯度为(hat{y}-y)。
三层神经网络的梯度推导
作业要求如下:
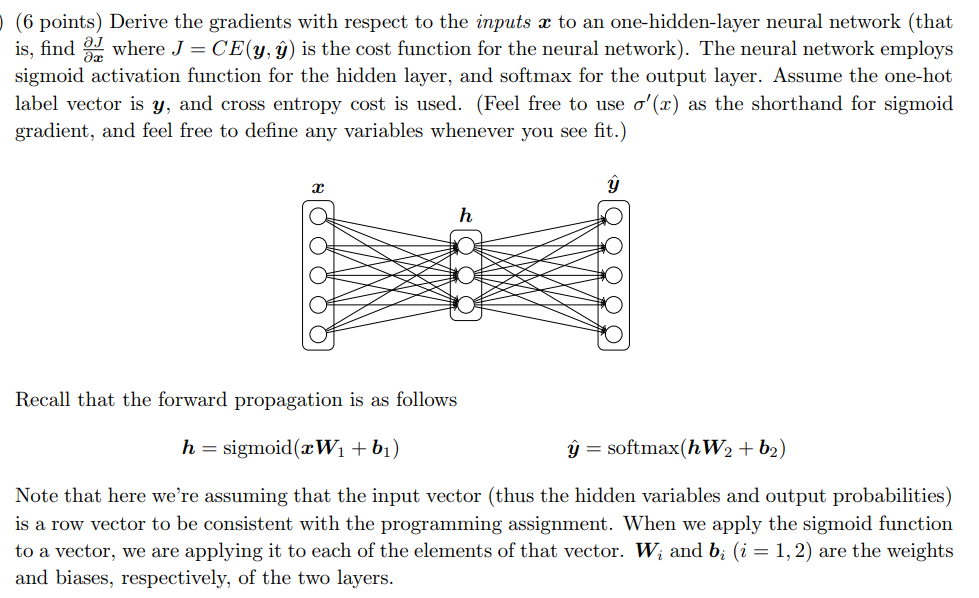
解析:本题要求推导(CE(y,hat{y}))对输入(x)的梯度。
解答:
