HDU 6055 17多校 Regular polygon（计算几何）

Problem Description

On a two-dimensional plane, give you n integer points. Your task is to figure out how many different regular polygon these points can make.

 

Input

The input file consists of several test cases. Each case the first line is a numbers N (N <= 500). The next N lines ,each line contain two number Xi and Yi(-100 <= xi,yi <= 100), means the points’ position.(the data assures no two points share the same position.)

 

Output

For each case, output a number means how many different regular polygon these points can make.

 

Sample Input

4

0 0

0 1

1 0

1 1

6

0 0

0 1

1 0

1 1

2 0

2 1

 

Sample Output

1

2

 

题意：给出n个坐标点（皆在格点上），求问这些点可以构成几个正多边形？

题解：

1.所有点皆在格点上只有一个情况，那便是正四边形

 2.任意枚举两个点，求出另两个点的坐标，来观察是否在给出的点中，若皆存在，cnt++。

求另两个坐标的方法：设已知两个点为a,b(a.x<b.x)，另两个点为c,d，设c是直接与b相连的，d是直接与a相连的

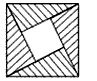
如图方法可以求出c-b,d-a的x,y变化分别为 disx=abs(a.y-b.y),disy=abs(a.x-b.x)，然后即可以通过一条边计算它左右两个正方形。具体见代码。

3.最后去重，因为一个四边形，它的四条边都计算过它一次，因此将最后的结果/4。

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<string.h>
using namespace std;

bool vis[205][205];
//把所有值都加100

struct node
{
    int x,y;
}point[505];

bool cmp(node a,node b)
{
    return a.x<b.x;
}

bool judge(node c)
{
    if(c.x>=0&&c.x<=200&&c.y>=0&&c.y<=200)
        if(vis[c.x][c.y])
            return true;
    return  false;
}


int main()
{
    int n,cnt;
    while(~scanf("%d",&n))
    {
        memset(vis,false,sizeof(vis));
        for(int i=0;i<n;i++)
        {
            scanf("%d%d",&point[i].x,&point[i].y);
            point[i].x+=100;
            point[i].y+=100;
            vis[point[i].x][point[i].y]=true;
        }
        sort(point,point+n,cmp);
        cnt=0;
        node a,b,c,d;
        int disx,disy;
        for(int i=0;i<n;i++)
        {
            for(int j=i+1;j<n;j++)
            {
                a=point[i];
                b=point[j];
                disx=abs(a.y-b.y);
                disy=abs(a.x-b.x);
                if(b.y<=a.y)
                {
                    //右上
                    c.x=b.x+disx;
                    c.y=b.y+disy;
                    d.x=a.x+disx;
                    d.y=a.y+disy;
                    if(judge(c)&&judge(d))
                        cnt++;
                    //左下
                    c.x=b.x-disx;
                    c.y=b.y-disy;
                    d.x=a.x-disx;
                    d.y=a.y-disy;
                    if(judge(c)&&judge(d))
                        cnt++;
                }
                else
                {
                    //右下
                    c.x=b.x+disx;
                    c.y=b.y-disy;
                    d.x=a.x+disx;
                    d.y=a.y-disy;
                    if(judge(c)&&judge(d))
                        cnt++;
                    //左上
                    c.x=b.x-disx;
                    c.y=b.y+disy;
                    d.x=a.x-disx;
                    d.y=a.y+disy;
                    if(judge(c)&&judge(d))
                        cnt++;
                }
            }
        }
        printf("%d
",cnt/4);
    }
    return 0;
}