拓展欧几里得算法

写在前面：

　　这篇博客是我在[◹]对 算术基本定理 的研究 中的一部分

by celebi-yoshi

目录

• 结论

• 证明

1. 已知正整数a，b，求一组p，q使满足p*a+q*b ≡ 0 (MOD GCD(a，b))

2. 已知正整数a，b，素数p，求一个整数x使满足x*a ≡ b (MOD p)

3. 已知正整数a，b，素数p，求一个整数x使满足a^x ≡ b (MOD p)

4. 已知正整数a，b，c，求一个整数x使满足x*a ≡ b (MOD c)

5. 已知正整数a，b，c，求一个整数x使满足a^x ≡ b (MOD c)

6. 解线性同余方程组 

结论

　　拓展欧几里得算法能解决的问题有：

① 已知正整数a，b，求一组p，q使满足p*a+q*b ≡ 0 (MOD GCD(a，b))

② 已知正整数a，b，素数p，求一个整数x使满足x*a ≡ b (MOD p)

③ 已知正整数a，b，素数p，求一个整数x使满足a^x ≡ b (MOD p)

④ 已知正整数a，b，c，求一个整数x使满足x*a ≡ b (MOD c)

⑤ 已知正整数a，b，c，求一个整数x使满足a^x ≡ b (MOD c)

⑥ 解线性方程组

证明

• 已知正整数a，b，求一组p，q使满足p*a+q*b ≡ 0 (MOD GCD(a，b))

　　现在已经有了a-b == GCD(a，b) * (n₁-n₂)，那就可以再来个直接点的

　　GCD(a，b) + (p*n₁+q*n₂) == GCD(a，b)

　　即p*a+q*b == GCD(a，b)

　　([◹]Bézout引理)

　　想要求出一组p，q∈Z，满足上式

 

　　首先套用欧几里得算法的逻辑：

　　　　结合算术基本定理，有

　　　　　　GCD(a，b) == P₁^min(a1,b1)P₂^min(a2,b2)......P_n^min(an,bn)

　　　　　　a MOD b == P₁^a1-b1P₂^a2-b2......P_n^an-bn(执行的条件为a_i>=b_i)

　　　　则能得到GCD(a，b) == GCD(b，a MOD b)

　　　　那么就有p*a+q*b == GCD(a，b) == GCD(b，a MOD b)

　　　　这样就可以写一个递归函数，一层一层MOD下去

　　　　这样化简，直到a_i MOD b_i == 0

　　　　即p*GCD(a，b) == GCD(a，b)，那么在最后一层里面p==1

所以在拓展欧几里得里面，bⁱ==0这一层中，aⁱ即为GCD(a，b)

　　(到此为止和欧几里得算法一模一样，我甚至是复制的欧几里得算法)

 

　　而如果想要求出p和q，那么有一个回溯的过程就好了

　　如何回溯得到p和q呢？

　　来找一下相邻的层数间p_i和p_i+1，q_i和q_i+1的关系

　　因为有p*a+q*b == GCD(a，b)

　　则在每一层中：

　　　　GCD(a，b)

　　　　　　== p_i*a+q_i*b

　　　　　　== p_i+1*b + q_i+1*(a MOD b)

　　　　　　== p_i+1*b + q_i+1*(a - (a/b)*b)

　　　　　　== p_i+1*b + q_i+1*a - q_i+1*(a/b)*b

　　　　　　== q_i+1*a + p_i+1*b - q_i+1*(a/b)*b

　　　　　　== q_i+1*a + (p_i+1 - q_i+1*(a/b))*b

　　即每层中p_i == q_i+1，q_i == p_i+1 - q_i+1*(a/b)

　　然后就可以回溯了！

　　然后就能写出不返回gcd，单纯求出一组p，q的拓展欧几里得了！

　　关于应用①中的多解问题，见[◹]拓展欧几里得算法的多解

C++：

#include<bits/stdc++.h>
#define OUT(x) cout<<#x<<":"<<x<<endl;

using namespace std;

int x,y;

void exgcd(int a,int b)
{
    if(!b){x=1;y=0;}
    else{
        exgcd(b,a%b);
        int tmp=x;
        x=y;y=tmp-(a/b)*y;
    }
}

int main(int argc,char *argv[],char *enc[])
{
    exgcd(12,17);
    OUT(x);OUT(y);
    return 0;
}

Java：

class Pony{
    
    static int x,y;

    static void exgcd(int a,int b)
    {
        if(b==0){x=1;y=0;}
        else{
            exgcd(b,a%b);
            int tmp=x;
            x=y;y=tmp-(a/b)*y;
        }
    }

    public static void main(String[] args) throws Exception
    {
        int a,b;a=54;b=27;
        exgcd(a,b);
        System.out.println(x+" "+y);
    }
}

　　上面这个版本是我写的，比较诡异，来个常见的版本

C++：

#include<bits/stdc++.h>
#define OUT(x) cout<<#x<<":"<<x<<endl;

using namespace std;

int x,y;

int exgcd(int a,int b)
{
    if(!b){
        x=1;y=0;
        return a;
    }
    int ret=exgcd(b,a%b);
    int tmp=x;
    x=y;y=tmp-(a/b)*y;
    return ret;
}

int main(int argc,char *argv[],char *enc[])
{
    OUT(exgcd(12,17));
    OUT(x);OUT(y);
    return 0;
}

Java：

class Pony{
    
    static int x,y;

    static int exgcd(int a,int b)
    {
        if(b==0){
            x=1;y=0;
            return a;
        }
        else{
            int ret=exgcd(b,a%b);
            int tmp=x;
            x=y;y=tmp-(a/b)*y;
            return ret;
        }
    }

    public static void main(String[] args) throws Exception
    {
        int a,b;a=54;b=27;
        exgcd(a,b);
        System.out.println(x+" "+y);
    }
}

　　仔细感受一下其中的差别啦~

• 已知正整数a，b，素数p，求一个整数x使满足x*a ≡ b (MOD p)

　　首先判断一下，如果a%p==0，那么无解

　　如果a%p!=0，那么必定有GCD(a，p)==1

　　

　　利用分治的方法，先利用上述①求得一个正整数x‘，使满足

　　　　x'*a + tmp*p ≡ gcd(a，p) (MOD p)

　　　　即x'*a ≡ 1 (MOD p)

　　然后易得

　　　　x=x'*b

　　　　x*a ≡ b (MOD p)

 C++：

#include<bits/stdc++.h>

using namespace std;

int a,b,p,x,y;

int exgcd(int a,int b)
{
    if(!b){
        x=1;y=0;
        return a;
    }
    int ret=exgcd(b,a%b);
    int tmp=x;
    x=y;y=tmp-(a/b)*y;
    return ret;
}

int main(int argc,char *argv[],char *enc[])
{
    scanf("%d%d%d",&a,&b,&p);
    if(exgcd(a,p)!=p){
        x*=b;
        printf("%d*%d ≡%d (mod %d)
",x,a,b,p);
    }
    else printf("NOPE
");
    
    return 0;
}

Java：

import java.util.Scanner;

class Pony{
    
    static int a,b,p,x,y;

    static int exgcd(int a,int b)
    {
        if(b==0){
            x=1;y=0;
            return a;
        }
        else{
            int ret=exgcd(b,a%b);
            int tmp=x;
            x=y;y=tmp-(a/b)*y;
            return ret;
        }
    }

    public static void main(String[] args) throws Exception
    {
        Scanner cin=new Scanner(System.in);

        a=cin.nextInt();
        b=cin.nextInt();
        p=cin.nextInt();
        if(exgcd(a,p)!=p){
            x*=b;
            System.out.printf("%d*%d ≡ %d (mod %d)
",x,a,b,p);
        }
        else System.out.println("NOPE");
    }
}

• 已知正整数a，b，素数p，求一个整数x使满足a^x ≡ b (MOD p)

　　详见[◹]Baby-step giant-step算法

• 已知正整数a，b，c，求一个整数x使满足x*a ≡ b (MOD c)

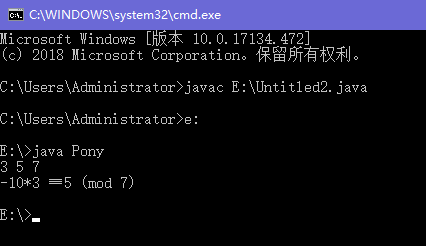
　　②中的无解是因为a%p==0，a为素数p的倍数

　　如果a不为p的倍数，gcd(a，p)==1

　　分治，结合①可以解得x'*a ≡ 1 (mod p)

　　在④中其实同理，只是有的时候gcd(a，c)不一定是1

　　我们想要gcd(a，c)为1

在同余中有一个神奇的性质：

A' == a'*d'

B' == b'*d'

C' == c'*d'

若A' ≡ B' (mod C')

则a'*d' ≡ b'*d' (mod c'*d')

即a' ≡ b' (mod c')

其中，a'，b'，c'，d'，A'，B'，C'都为整数

暂且叫这条性质为放缩

　　求解x*a ≡ b (MOD c)，想要延续②中的思路

　　如果gcd(a，c)不是b的因子或b不等于0，那么可以知道gcd(a，c)!=1，而方程一定无解(下面有证明)

　　而如果gcd(a，c)为b的因子或b等于0，那么有

　　　　a==a'*gcd(a，c)

　　　　c==c'*gcd(a，c)

　　　　b==b'*gcd(a，c)

　　　　有x*a ≡ b (MOD c)

　　　　则x*a'*gcd(a，c) ≡ b'*gcd(a，c) (MOD c'*gcd(a，c))

　　　　根据放缩，即x*a' ≡ b' (MOD c')

　　　　此时，gcd(a'，c')==1

　　这样一来，就完美转化为了②中的思路，可以求解了

　　但是，如果b中没有gcd(a，c)这个因子或b不等于0，是否就没有解呢？

　　答案是，没有解，一定没有解

同余方程x*a ≡ b (mod c)有解x的充分必要条件是b%gcd(a，c)==0

　　证明如下：

　　　　设整数A，C，a，b，c，d，其中A==a*d，c==c*d，abcd两两互质

我们想要通过缩放来得到gcd(a，c)==1，这是我们的目标

　　　　设满足A ≡ b (mod C)

　　　　则a*d ≡ b (mod c*d)

　　　　根据放缩，有a ≡ b/d (mod c)

　　　　∵abcd两两互质

　　　　∴d不是b的因数且b不等于0

　　　　∴b/d不是整数

　　　　而在同余方程中的每个变元都必须为整数

　　　　所以出现分数的情况视为违规

　　　　则这个同余式不成立

　　　　所以同余方程x*a ≡ b (mod c)有解x的充分必要条件是b%gcd(a，c)==0

 

　　由以上证明可以看出来在同余方程中，出现无解情况的本质

 

代码如下：

C++：

#include<bits/stdc++.h>

using namespace std;

int a,b,c,x,y;
int times;

int exgcd(int a,int b)
{
    if(!b){
        x=1;y=0;
        return a;
    }
    int ret=exgcd(b,a%b);
    int tmp=x;
    x=y;y=tmp-(a/b)*y;
    return ret;
}

int main(int argc,char *argv[],char *enc[])
{
    scanf("%d%d%d",&a,&b,&c);
    
    int tmp=exgcd(a,c);
    
    if(b%tmp!=0) printf("NOPE
");
    else{
        while(b%tmp==0){
            a/=tmp;
            b/=tmp;
            c/=tmp;
            ++times;
        }
        
        if(tmp!=c){
            x*=b;
            printf("%d*%d ≡ %d (mod %d)
",x,a*times*tmp,b*times*tmp,c*times*tmp);
        }
        else printf("NOPE
");
    }
    
    return 0;
}

Java：

import java.util.Scanner;

class Pony{
    
    static int a,b,c,x,y;
    static int times;

    static int exgcd(int a,int b)
    {
        if(b==0){
            x=1;y=0;
            return a;
        }
        else{
            int ret=exgcd(b,a%b);
            int tmp=x;
            x=y;y=tmp-(a/b)*y;
            return ret;
        }
    }

    public static void main(String[] args) throws Exception
    {
        Scanner cin=new Scanner(System.in);

        a=cin.nextInt();
        b=cin.nextInt();
        c=cin.nextInt();

        int tmp=exgcd(a,c);

        if(b%tmp!=0) System.out.println("NOPE");
        else{
            while(b%tmp==0){
                a/=tmp;
                b/=tmp;
                c/=tmp;
                ++times;
            }

            if(tmp!=c){
                x*=b;
                System.out.printf("%d*%d ≡ %d (mod %d)
",x,a*times*tmp,b*times*tmp,c*times*tmp);
            }
            else System.out.println("NOPE");
        }
    }
}

• 已知正整数a，b，c，求一个整数x使满足a^x ≡ b (MOD c)

　　详见[◹]拓展Baby-step giant-step算法

• 解线性同余方程组

　　俗称的拓展中国剩余定理(虽然这样叫很不准确)

　　详见[◹]解线性同余方程组