2019 Petrozavodsk Winter Camp, Yandex Cup C. Diverse Singing 上下界网络流

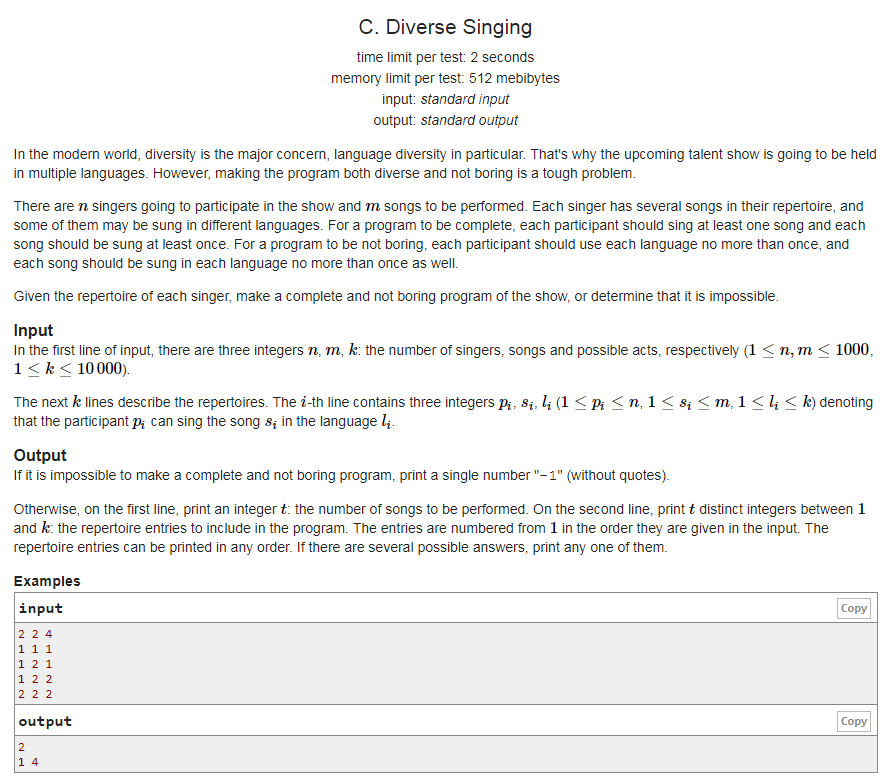
建图一共建四层 第一层为N个歌手 第二层为{pi,li} 第三层为{si,li} 第四层为M首歌

除了S和第一层与第三层与T之间的边为[1,INF] 其他边均为[0,1]

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef int JQK;
const JQK INF = 1000000005;
struct node {
        int p, s, l;
        bool operator <(const node &rhs) const {
                if (p != rhs.p)
                        return p > rhs.p;
                else {
                        if (s != rhs.s)
                                return s > rhs.s;
                        else
                                return l > rhs.l;
                }
        }
} nodecnt;
int n, m, k, s1, t1, s2, t2;
map<pair<int, int>, int> pl, sl;
map<int, pair<int, int> > plb, slb;
map<node, int> psl;
vector<int> anser;
namespace dinic {
        const int MAXN = 30050;
        const int MAXM = 100050;
        const JQK INF = 1000000050;
        int Head[MAXN], cur[MAXN], lev[MAXN], to[MAXM << 1], nxt[MAXM << 1], ed = 1;
        int S, T, SS, TT, MAXP;
        JQK f[MAXM << 1], totflow[MAXN];
        inline void addedge(int u, int v, JQK cap) {
                to[++ed] = v;
                nxt[ed] = Head[u];
                Head[u] = ed;
                f[ed] = cap;
                to[++ed] = u;
                nxt[ed] = Head[v];
                Head[v] = ed;
                f[ed] = 0;
                return;
        }
        inline void add(int u, int v, JQK caplow, JQK captop) {
                addedge(u, v, captop - caplow);
                totflow[u] -= caplow, totflow[v] += caplow;
                return ;
        }
        inline bool BFS() {
                int u;
                for (int i = 0; i <= MAXP + 1; i++) {
                        lev[i] = -1;
                }
                //memset(lev, -1, sizeof(lev));
                queue<int>q;
                lev[S] = 0;
                q.push(S);
                while (q.size()) {
                        u = q.front();
                        q.pop();
                        for (int i = Head[u]; i; i = nxt[i])
                                if (f[i] && lev[to[i]] == -1) {
                                        lev[to[i]] = lev[u] + 1;
                                        q.push(to[i]);
                                        /*
                                        if (to[i] == T)
                                        {
                                                return 1;
                                        }
                                        magic one way optimize
                                        */
                                }
                }
                for (int i = 0; i <= MAXP + 1; i++) {
                        cur[i] = Head[i];
                }
                //memcpy(cur, Head, sizeof Head);
                return lev[T] != -1;
        }
        inline JQK DFS(int u, JQK maxf) {
                if (u == T || !maxf) {
                        return maxf;
                }
                JQK cnt = 0, tem;
                for (int &i = cur[u]; i; i = nxt[i])
                        if (f[i] && lev[to[i]] == lev[u] + 1) {
                                tem = DFS(to[i], min(maxf, f[i]));
                                maxf -= tem;
                                f[i] -= tem;
                                f[i ^ 1] += tem;
                                cnt += tem;
                                if (!maxf) {
                                        break;
                                }
                        }
                if (!cnt) {
                        lev[u] = -1;
                }
                return cnt;
        }
        JQK Dinic() {
                JQK ans = 0;
                while (BFS()) {
                        ans += DFS(S, INF);
                }
                return ans;
        }
        void del(int x) {
                for (int i = Head[x]; i; i = nxt[i])
                        f[i] = f[i ^ 1] = 0;
        }
        void init(int S1, int T1, int S2, int T2) {
                for (int i = 0; i <= MAXP + 1; i++) {
                        totflow[i] = Head[i] = 0;
                }
                ed = 1;
                S = S1;
                T = T1;
                SS = S2;
                TT = T2;
                return;
        }
        inline JQK pushdownflow(int x) {
                JQK sum = 0;
                for (int i = 1; i <= x; i++) {
                        if (totflow[i] > 0) {
                                addedge(SS, i, totflow[i]);
                                sum += totflow[i];
                        } else if (totflow[i] < 0) {
                                addedge(i, TT, -totflow[i]);
                        }
                }
                return sum;//sum==dinic 循环流有解
        }
        JQK work() { //有源汇最大流
                JQK ans = 0;
                JQK sum = pushdownflow(TT - 2);
                addedge(T, S, INF);
                swap(S, SS), swap(T, TT);
                if (sum != Dinic()) { //Dinic(SS,TT) 求出一个有源汇有上下界可行流.此时的流不一定最大.
                        cout << -1 << endl;
                        return 0;
                }
                ans = f[ed]; //可行流流量
                f[ed] = f[ed ^ 1] = 0;
                swap(S, SS), swap(T, TT); //Dinic(S,T)
                ans += Dinic();//新增广出的s-t流量
                cout << ans << endl;
                for (int i = n + m + 1; i <= n + m + k; i++) {
                        for (int j = Head[i]; j; j = nxt[j]) {
                                int v = to[j];
                                if (v >= n + m + k + 1 && v <= n + m + 2 * k && f[j] == 0) {
                                        nodecnt.p = plb[i].first;
                                        nodecnt.s = slb[v].first;
                                        nodecnt.l = slb[v].second;
                                        anser.push_back(psl[nodecnt]);
                                }
                        }
                }
                sort(anser.begin(), anser.end());
                for (int v : anser) {
                        cout << v << " ";
                }
                return ans;
        }
}
int main() {
        int u, v;
        JQK c;
        scanf("%d %d %d", &n, &m, &k);
        dinic::MAXP = n + m + 2 * k + 5;
        s1 = n + m + 2 * k + 1;
        t1 = s1 + 1;
        s2 = t1 + 1;
        t2 = s2 + 1;
        dinic::init(s1, t1, s2, t2); //S T SS TT
        for (int i = 1; i <= n; i++)
                dinic::add(s1, i, 1, INF);
        for (int i = n + 1; i <= n + m; i++)
                dinic::add(i, t1, 1, INF);
        for (int i = 1; i <= k; i++) {
                scanf("%d %d %d", &u, &v, &c);
                nodecnt.p = u, nodecnt.s = v, nodecnt.l = c;
                if (!psl[nodecnt])
                        psl[nodecnt] = i;
                if (!pl[make_pair(u, c)]) {
                        pl[make_pair(u, c)] = n + m + i;
                        plb[n + m + i] = make_pair(u, c);
                        dinic::add(u, n + m + i, 0, 1);
                }
                if (!sl[make_pair(v, c)]) {
                        sl[make_pair(v, c)] = n + m + k + i;
                        slb[n + m + k + i] = make_pair(v, c);
                        dinic::add(n + m + k + i, n + v, 0, 1);
                }
                dinic::add(pl[make_pair(u, c)], sl[make_pair(v, c)], 0, 1);
        }
        dinic::work();
        return 0;
}