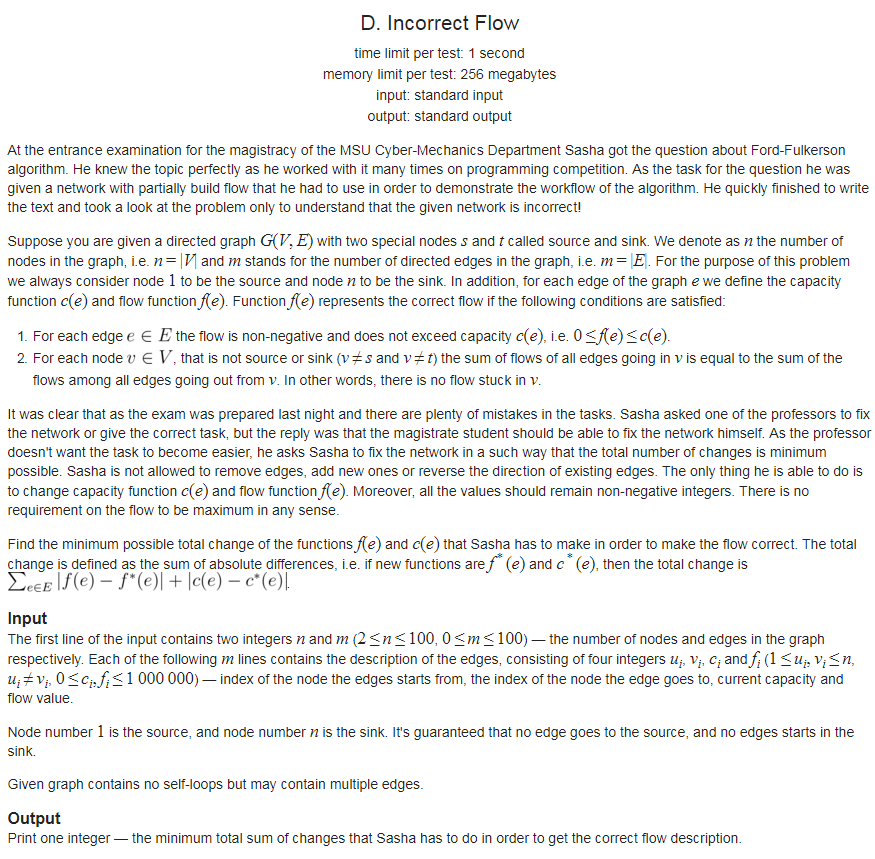
给你一个网络流的图 图中可能会有流量不平衡和流量>容量的情况存在
每调整一单位的流量/容量 需要一个单位的花费
问最少需要多少花费使得原图调整为正确(可行)的网络流
设当前边信息为(u,v,f,c) 即从u到v有一条流量为f,容量为c的有向边
设加的边信息为[u,v,f,c] 即加一条从u到v有一条容量为f,单位费用为c的有向边
首先如果源汇的流量不平衡的话 要加一条边[T,S,INF,0]使得源汇流量平衡
接下来分情况讨论:
①:流量f>容量c
首先ans+=f-c 因为必须调整f-c个单位的流之后 才能使该边合法
加边[u,v,INF,2] 这条边的意思为f=c时 提高f需要2的花费(需要同时提高c)
加边[v,u,f-c,0] 可用作减少流量
加边[v,u,c,1] 可用作减少流量
边[u,v,INF,2]很好理解 但边[v,u,f-c,0]和[v,u,c,1]该如何理解呢
首先我们分析调整完后该边f的流量有下列情况 1.[0,c] 2.[c,f] 3.[f,INF]
第一种情况c不需要调整 要调整的是f 因为我们预先支付了f-c费用 所以f~c阶段的花费是0 而0~c的阶段单位费用为1
第二种情况c和f同时需要调整 但是总费用是f-c 我们只需要利用[v,u,f-c,0]调整到想要的f即可
第三者情况c和f也同时需要调整 但是f不会减小 所以后面两种边就无效了
所以这三种边就可以包括f的全部情况
②:流量f<=容量c
加边[u,v,INF,2] 这条边的意思为f=c时 提高一单位f需要2的花费(需要同时提高c)
加边[u,v,c-f,1] f~c这段单位花费为1
加边[v,u,f,1] 0~f这段单位花费为1
加完费用流的边之后 对于每条(u,v,f,c) 都needflow[u]-=f needflow[v]+=f
对于每个点(包括源汇)
needflow[i]>0则加[SS,i,needflow[i],0] needflow[i]<0则加[i,TT,-needflow[i],0]
最后跑一次SS到TT的最小费用流 加上之前的ans 即为答案