HDU 6103 Kirinriki【尺取法】【思维题】【好题】

Kirinriki

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 456    Accepted Submission(s): 160

Problem Description

We define the distance of two strings A and B with same length n is
disA,B=∑i=0n−1|Ai−Bn−1−i|
The difference between the two characters is defined as the difference in ASCII.
You should find the maximum length of two non-overlapping substrings in given string S, and the distance between them are less then or equal to m.

 

Input

The first line of the input gives the number of test cases T; T test cases follow.
Each case begins with one line with one integers m : the limit distance of substring.
Then a string S follow.

Limits
T≤100
0≤m≤5000
Each character in the string is lowercase letter, 2≤|S|≤5000
∑|S|≤20000

 

Output

For each test case output one interge denotes the answer : the maximum length of the substring.

 

Sample Input

1 5 abcdefedcb

 

Sample Output

5

Hint

[0, 4] abcde [5, 9] fedcb The distance between them is abs('a' - 'b') + abs('b' - 'c') + abs('c' - 'd') + abs('d' - 'e') + abs('e' - 'f') = 5

 

Source

2017 Multi-University Training Contest - Team 6

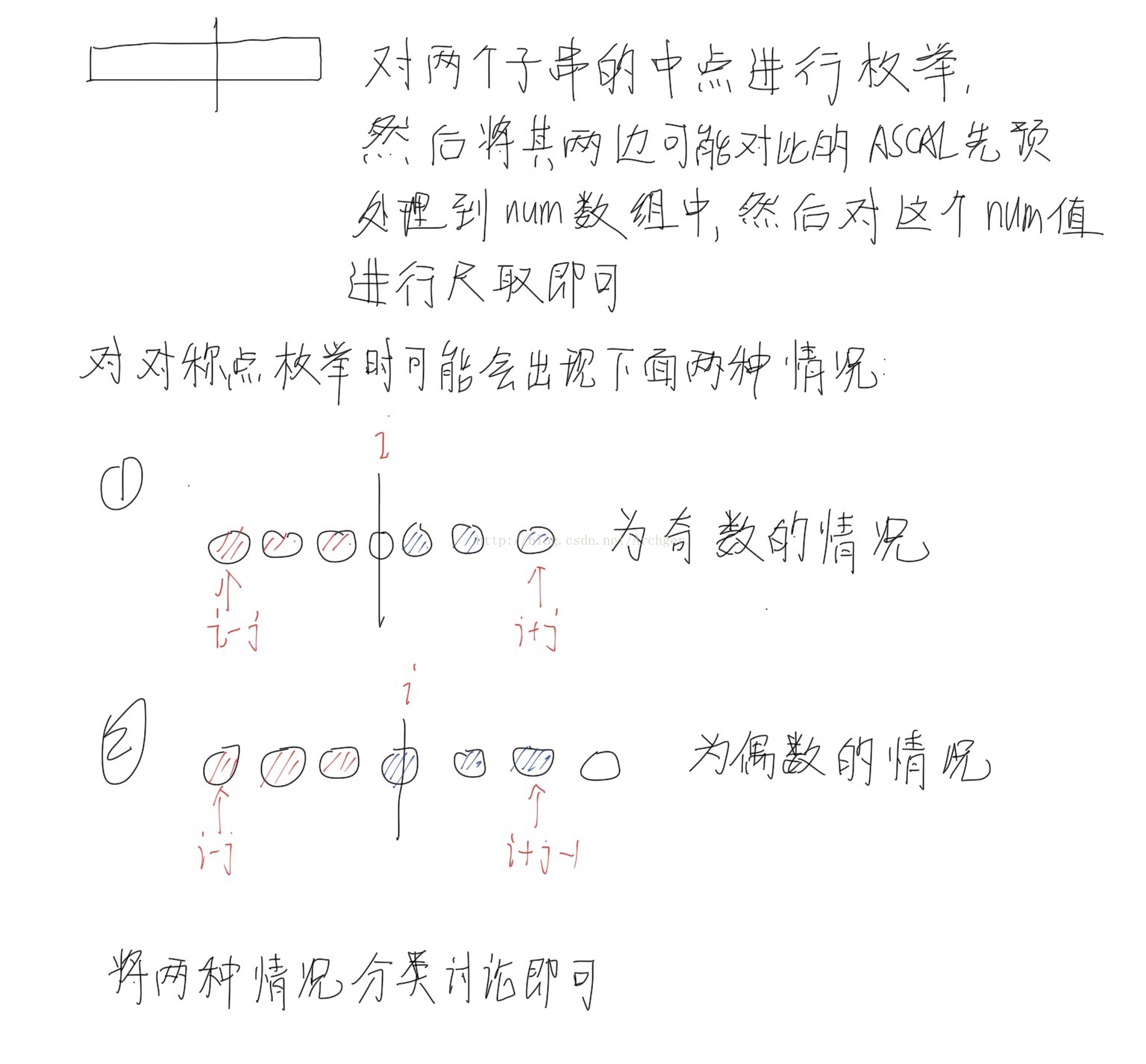
题意：

给出字符串s，寻找其两个长度相同且不重叠的子串，满足其每位的ascil差值之和不大于m，且长度最长。

思路：

因为字符串的长度为5000，所以可以枚举两个子串的对称轴，然后对其区间进行尺取法，这样只需要o(n^2)的复杂度即可。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <algorithm>
#include <queue>
#include <map>
using namespace std;
const int INF = 0x3f3f3f3f;
const int maxn = 5010;

char a[maxn], num[maxn];
int m;

int solve(int len)
{
	int s = 0, t = 0, ans = 0, sum = 0;
	while (1)
	{
		while (sum + num[t] <= m && t < len)
		{
			sum += num[t];
			ans = max(t - s + 1, ans);
			t++;
		}
		sum -= num[s++];
		if (s >= len) break;
	}
	return ans;
}

int main()
{
	int t;
	scanf("%d", &t);
	while (t--)
	{
		int len, res = 0;
		scanf("%d", &m);
		scanf("%s", a);
		len = strlen(a);
		for (int i = 0; i <= len; i++)	//枚举折的中点
		{
			int cnt = 0;
			for (int j = 1; j + i < len && i - j >= 0; j++)	//枚举奇数情况
				num[cnt++] = abs(a[j + i] - a[i - j]);
			res = max(res, solve(cnt));
		}
		for (int i = 0; i <= len; i++)	//枚举折的中点
		{
			int cnt = 0;
			for (int j = 1; j + i - 1 < len && i - j >= 0; j++)	//枚举偶数情况
				num[cnt++] = abs(a[j + i - 1] - a[i - j]);
			res = max(res, solve(cnt));
		}
		printf("%d
", res);
	}
	return 0;
}